Basit Eşitsizlikler Konu Anlatımı

Matematikte eşitsizlikler, bir ifadeyi başka bir ifadeden küçük, büyük, küçük eşit veya büyük eşit olarak tanımlayan matematiksel ifadelerdir. TYT Matematik sınavında sıkça karşılaşılan basit eşitsizlikler, bilinmeyenli ifadeleri karşılaştırmayı ve çözüm kümelerini belirlemeyi sağlar.

Eşitsizlikler, günlük yaşamda ölçümler, bütçe hesaplamaları, hız problemleri ve optimizasyon işlemleri gibi birçok alanda kullanılır.

Bu bölümde eşitsizlik kavramını, aralık gösterimini, temel özelliklerini ve çözüm kümesini bulma yöntemlerini detaylıca ele alacağız.

Şimdi, eşitsizlikler konusuna giriş yapalım! 🚀📚

Eşitsizlik Nedir?

Eşitsizlik, iki matematiksel ifadenin birbirine eşit olmadığı durumları ifade eden bir matematiksel ilişki biçimidir.

Eşitsizlikler şu sembollerle gösterilir:

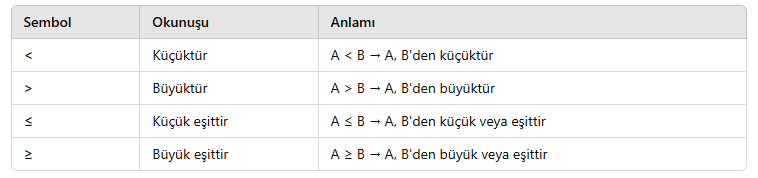
Örnekler:

• 5 < 8 → “5, 8’den küçüktür.”
• x + 2 > 7 → “x sayısına 2 eklenirse, sonuç 7’den büyük olur.”
• 3x – 4 ≤ 5 → “3x – 4 ifadesi en fazla 5 olabilir.”

Aralık Kavramı

Eşitsizliklerin çözüm kümeleri aralık (interval) gösterimi ile ifade edilir. Aralıklar kapalı (kapsar) veya açık (kapsamaz) olabilir.

Aralık Gösterimi Tablosu

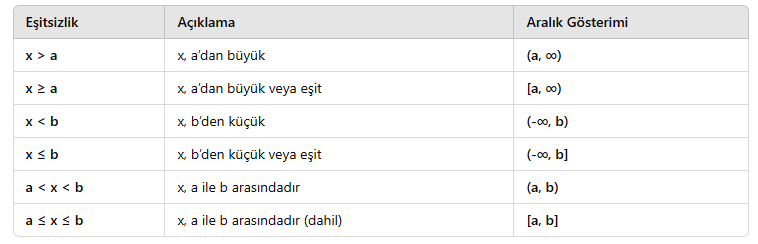
Örnekler:

• x > 3 için (3, ∞)
• x ≤ -2 için (-∞, -2]
• -1 < x < 4 için (-1, 4)

Eşitsizliklerin Özellikleri

Eşitsizlikler temel cebirsel kurallara uyar. Ancak, özel durumlar içerirler.

Özellik 1: Eşitsizliğin Her İki Tarafına Aynı Sayıyı Ekleyebiliriz veya Çıkarabiliriz

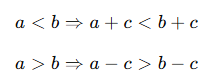
Örnek:
4 < 7
Her iki tarafa +3 ekleyelim → 4 + 3 < 7 + 3 → 7 < 10 (Eşitsizlik değişmedi)

Özellik 2: Eşitsizliğin Her İki Tarafını Aynı Sayı ile Çarpabiliriz

• Pozitif sayı ile çarpıldığında yön değişmez.
• Negatif sayı ile çarpıldığında yön ters döner.

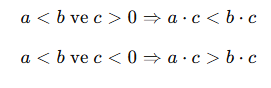
Örnek:
3 < 5 eşitsizliğini (-2) ile çarparsak:

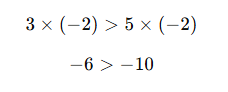
Yön değişti!

Özellik 3: Eşitsizliğin Her İki Tarafını Aynı Pozitif Sayıya Bölebiliriz

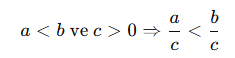
Örnek:
10 < 20
Her iki tarafı 2’ye bölelim:

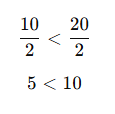
Yön değişmedi!

Özellik 4: Eşitsizliğin Her İki Tarafını Aynı Negatif Sayıya Bölersek Yön Değişir

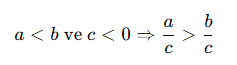
Örnek:
-15 < -5
Her iki tarafı (-5) ile bölelim:

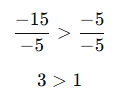
Yön değişti!

4. Basit Eşitsizliklerin Çözüm Kümesi Nasıl Bulunur?

Adımlar:

1. Eşitsizlikte bilinmeyeni yalnız bırakın.
2. Dört işlem kurallarına dikkat ederek eşitsizliği çözelim.
3. Çözüm kümesini aralık olarak gösterelim.

Örnek:

Adım 1: 5’i karşıya atalım:

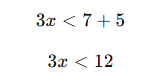
Adım 2: Her iki tarafı 3’e bölelim:

Adım 3: Aralık gösterimi:

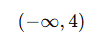
Örnek Sorular

1. x + 4 > 9 eşitsizliğinin çözüm kümesi nedir?
A) (-∞, 5)
B) (5, ∞)
C) (-∞, -5)
D) (-∞, 4]

2. 3x – 2 ≤ 7 eşitsizliğini çözün.
A) x ≤ 9/3
B) x ≤ 3
C) x ≥ 3
D) x ≤ 7

3. 5 – 2x ≥ 1 eşitsizliğini çözün.
A) x ≤ 2
B) x ≥ 2
C) x ≥ 4
D) x ≤ 3

TYT Matematik – Basit Eşitsizlikler Ünitesi Testi

Aşağıdaki test, Basit Eşitsizlikler konusunu pekiştirmenize yardımcı olacaktır. Soruları dikkatlice okuyup en doğru seçeneği işaretleyin.

1. Aşağıdaki eşitsizliklerden hangisi doğru bir ifadedir?

A) 7 < 5
B) -3 > -2
C) 8 ≤ 8
D) 10 ≥ 12

2. x – 3 > 5 eşitsizliğinin çözüm kümesi nedir?

A) x > 2
B) x > 5
C) x > 8
D) x < 8

3. 2x + 4 ≤ 10 eşitsizliğini çözün.

A) x ≤ 3
B) x ≥ 3
C) x ≤ 2
D) x ≥ 5

4. -3x + 7 < 1 eşitsizliğini çözün.

A) x > 2
B) x < 2
C) x > -2
D) x < -2

5. Aşağıdaki eşitsizliklerden hangisi çözüm kümesi olarak (-∞, 4] aralığını verir?

A) x < 4
B) x ≥ 4
C) x ≤ 4
D) x > 4

6. 5 – 2x ≥ 1 eşitsizliğini sağlayan x değerleri hangi aralıktadır?

A) x ≤ 2
B) x ≥ 2
C) x ≥ -2
D) x ≤ -2

7. Aşağıdaki eşitsizliklerden hangisi çözüm kümesi (-∞, 7) olan bir eşitsizliktir?

A) x ≤ 7
B) x < 7
C) x > 7
D) x ≥ 7

8. 4x – 2 > 6 eşitsizliğini çözün.

A) x > 2
B) x ≥ 2
C) x < 2
D) x ≤ 2

9. -2x + 8 ≥ 4 eşitsizliğini sağlayan x değerleri hangi aralıktadır?

A) x ≥ 2
B) x ≤ 2
C) x ≥ -2
D) x ≤ -4

10. -x + 3 < 5 eşitsizliğini sağlayan x değerleri hangi aralıktadır?

A) x > -2
B) x < -2
C) x > 2
D) x < 2

Cevap Anahtarı

1. C
2. C
3. A
4. D
5. C
6. A
7. B
8. A
9. B
10. C

Bu testi çözüp kendinizi değerlendirebilirsiniz. Hatalı olduğunuz soruları tekrar gözden geçirmeyi unutmayın! 🚀📚