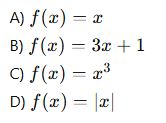AYT Matematik Fonskiyonlar Konu Anlatımı

Fonksiyonlar, matematikte “her girdiye bir çıktının karşılık geldiği” yapıları tanımlar.
AYT’de bu konu:

• Fonksiyon tanımı

• Gösterim yolları

• Özellikler (birebir, örten, sabit…)

• Fonksiyonlarda işlem

• Bileşke ve ters fonksiyon

• Grafiksel yorum
  başlıklarıyla geniş biçimde karşımıza çıkar.

Fonksiyonlar ayrıca polinom, trigonometri, türev, integral gibi AYT’nin ileri konularının da temelini oluşturur.

🔹 Fonksiyonlar Ünitesinin Alt Başlıkları:

1. Fonksiyon Tanımı ve Gösterimleri

2. Birebir, Örten, Sabit Fonksiyonlar

3. Fonksiyonlarda Dört İşlem

4. Bileşke Fonksiyon

5. Ters Fonksiyon

6. Fonksiyon Grafikleri ve Yorumu

🎯 AYT’de Bu Konu Nasıl Sorulur?

• Verilen fonksiyonun girdi/çıktı eşlemesi

• Fonksiyonun birebirliği – örtenliği

• Bileşke veya ters fonksiyon değeri

• Grafiksel yorum, tanım – değer kümeleri

• Karmaşık gösterim ve işlem içeren sorular

Fonksiyon Tanımı ve Gösterimleri

📘 Fonksiyon Nedir?

Fonksiyon, bir kümenin her elemanını başka bir kümeye belirli bir kuralla eşleyen bir yapıdır.
Her girişe (tanım kümesinden) yalnızca bir çıkış (değer kümesinden) karşılık gelir.

🧠 Temel Tanım:

🎯 Fonksiyon Olma Koşulu:

Bir fonksiyon olabilmesi için:

• Tanım kümesindeki her eleman eşlenmeli

• Her eleman sadece bir elemanla eşlenmeli

• Değer kümesinde birden fazla eşleşme olabilir

🔢 f(x) Gösterimi:

Fonksiyonlar genellikle şöyle gösterilir:

Burada:

• x → giriş

• f(x) → çıkış

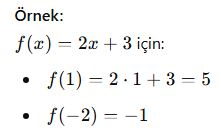
✏️ Gösterim Yöntemleri:

📌 Dikkat Edilecekler:

Mini Alıştırmalar:

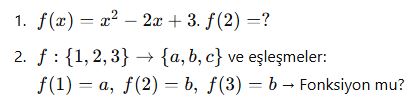
3. “Bir eleman 2 farklı yere gidiyorsa bu eşleme…”
A) Fonksiyondur B) Fonksiyon değildir

✅ Cevaplar:

2. ✅ Fonksiyondur (aynı çıkış olabilir)

3. B → Fonksiyon değildir

Birebir, Örten ve Sabit Fonksiyonlar

📘 A. Birebir Fonksiyon (1–1)

Bir fonksiyon, farklı girdilere farklı çıktılar veriyorsa birebirdir.
Yani:

📘 B. Örten Fonksiyon (Onto)

Bir fonksiyonun görüntü kümesi, değer kümesini tamamen kaplıyorsa fonksiyon örten (onto) olur.

Yani:

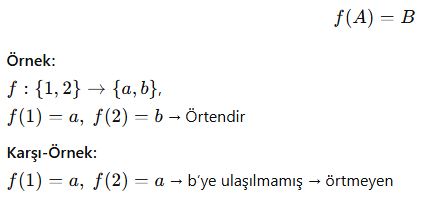
📘 C. Sabit Fonksiyon

Fonksiyonun tüm girişleri aynı çıktıyı veriyorsa sabittir.

Yani:

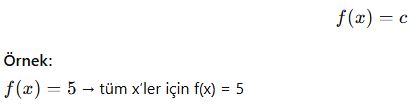
🎯 Şematik Yorum:

• Birebir: A’daki her eleman farklı B elemanına gider

• Örten: B’de boşa çıkan eleman yok

• Sabit: Tüm oklar B’de tek bir noktaya gider

📌 Dikkat Edilecekler:

✅ Cevaplar:

1. ✅ Evet, çünkü farklı x’ler farklı sonuç verir

2. ❌ Hayır, çünkü a ve b’ye ulaşılmış ama b iki kez alınmış → yine de örtendir ✅

3. Sabit fonksiyon

Fonksiyonlarda Dört İşlem

📘 A. İşlem Tanımları

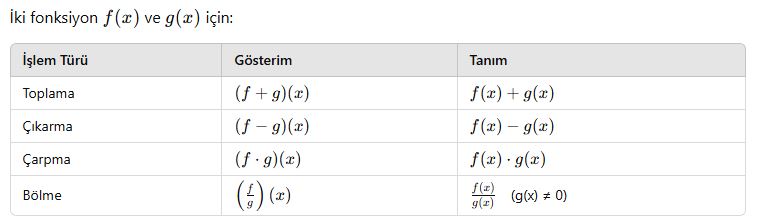
Bu işlemler normal cebirsel işlemler gibi yapılır, sadece her işlem fonksiyonların değerleri üzerinden yürür.

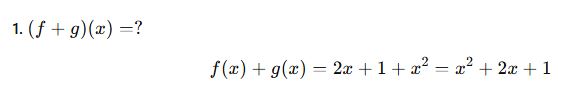
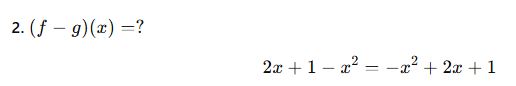
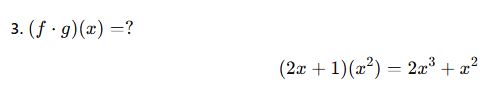
🔎 Tanım Kümesine Dikkat!

• Fonksiyonların tanım kümeleri ortak olmalı

• Bölme işleminde payda sıfır olmamalı

📌 Özel Durum:

Verilen iki fonksiyon:

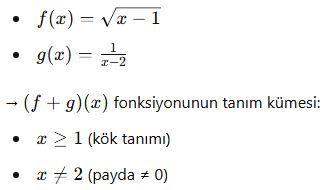
→ Ortak tanım:

Mini Alıştırmalar:

Verilen:

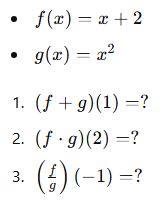
✅ Cevaplar:

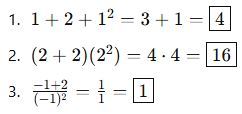
Bileşke Fonksiyon (f ∘ g)

📘 Tanım:

Bileşke fonksiyon, f∘g biçiminde yazılır ve:

Yani önce g(x) bulunur, sonra bu değer f’ye gönderilir.

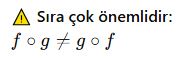
🎯 Adım Adım Uygulama:

1. İçerideki fonksiyon (g(x)) bulunur

2. Bu sonuç dıştaki fonksiyona (f) verilir

3. Sonuç, bileşke fonksiyonun değeridir

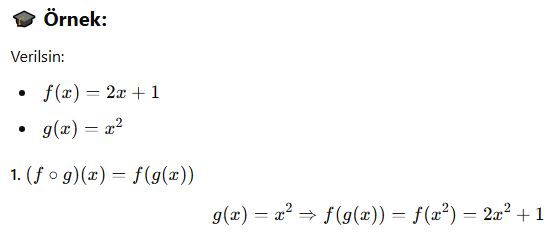
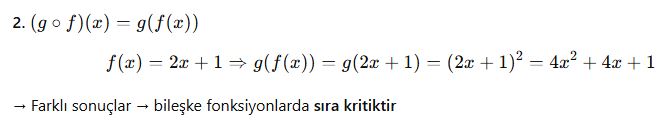
📌 Tanım Kümesine Dikkat:

Bileşke fonksiyonun tanım kümesi:

Yani önce g tanımlı olmalı, sonra sonucu f kabul etmeli

Mini Alıştırmalar:

Verilen:

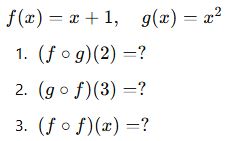
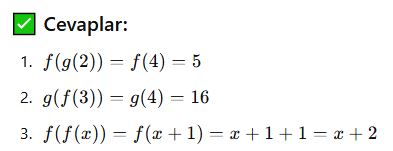
Ters Fonksiyon (f⁻¹)

📘 Ters Fonksiyon Nedir?

Bir fonksiyon, girdiyi çıktıya çevirir:

Ters fonksiyon ise çıktıyı girdiye geri götürür:

Yani:

🎯 Ters Fonksiyonun Tanım Koşulu:

Bir fonksiyonun tersinin olması için:

✅ Birebir (1–1)
✅ Örten (onto)

olması gerekir.
Yani her çıktının tek bir karşılığı olmalı.

🧠 Ters Fonksiyon Nasıl Bulunur?

Adım adım:

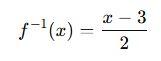
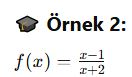
→ Bu tür fonksiyonların tersini bulmak için payda – payı karıştırmadan dikkatlice çözüm yapılır.

🔁 Tersin Tersi:

Tersin tersi, kendisidir.

📌 Terslik Kontrolü:

İki fonksiyon birbirinin tersi ise:

Bu kontrolle sınavda doğruluğu test edebilirsin.

Fonksiyon Grafikleri ve Yorumu

📘 Fonksiyonun Grafiği Nedir?

Fonksiyonun grafiği, her x için f(x) çıktısını gösteren (x, y) noktalarının oluşturduğu çizimdir.
Bu grafik, fonksiyonun:

• Tanım kümesini

• Artma – azalma aralıklarını

• Tersinin olup olmadığını

• Birebir – örten özelliklerini
  gözle değerlendirmemizi sağlar.

🎯 Grafik Üzerinden Yorumlama Kuralları

🔹 1. Düşey Doğru Testi (Fonksiyon mu?)

Grafiğe çizilen her düşey doğru, grafiği en fazla bir noktada kesiyorsa, bu eğri bir fonksiyon grafiğidir.

✅ Oluyorsa → fonksiyondur
❌ 2 noktada kesiyorsa → fonksiyon değildir

🔹 2. Birebirlik – Yatay Doğru Testi

Grafiğe çizilen her yatay doğru, grafiği en fazla bir noktada kesiyorsa, fonksiyon birebirdir.

🔹 3. Tersinin Grafiği

• f(x) fonksiyonunun tersinin grafiği, y = x doğrusuna göre simetrik olur.

• Yani (a, b) noktası varsa, tersinde (b, a) olur.

🎓 Örnek:

Aşağıdaki fonksiyon grafiklerinden hangisi birebir değildir?

📈 Grafiksel Özellikler:

Mini Alıştırmalar:

1. Düşey doğru testi hangi özelliği kontrol eder?

2. f(x)=∣x∣ fonksiyonunun ters fonksiyonu var mı?

3. Grafikte (3, 5) noktası varsa, tersinde hangi nokta vardır?

✅ Cevaplar:

1. Fonksiyon olup olmadığını

2. ❌ Yok, çünkü birebir değil

3. (5,3)

Ayt Fonksiyonlar Deneme Testi

Her soru farklı bir alt başlıktan seçilmiştir.
Cevap anahtarı en altta.

1. (Fonksiyon Tanımı)

Aşağıdaki eşleşmelerden hangisi fonksiyondur?

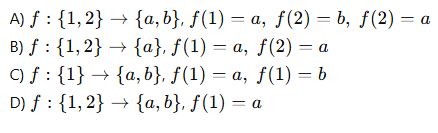
2. (Birebir Fonksiyon)

Aşağıdaki fonksiyonlardan hangisi birebir değildir?

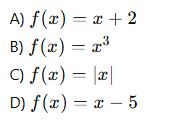
3. (Örtenlik)

A) Evet
B) Hayır
C) Birebir ve örten
D) Sabit fonksiyon

4. (Sabit Fonksiyon)

Aşağıdakilerden hangisi sabit fonksiyondur?

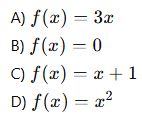
5. (Fonksiyon İşlemleri)

Verilsin:

6. (Fonksiyon İşlemleri)

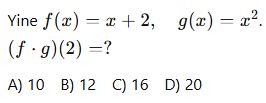
7. (Bileşke Fonksiyon)

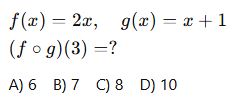
8. (Ters Fonksiyon)

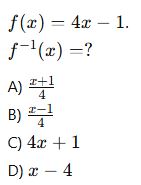
9. (Fonksiyonun Tersi Vardır mı?)

Aşağıdaki fonksiyonlardan hangisinin tersi yoktur?

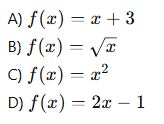
10. (Grafik Yorumu)

Aşağıdakilerden hangisi birebir fonksiyon değildir?