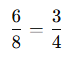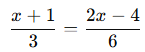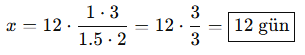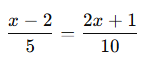İçindekiler
AYT Matematik Oran Orantı Konu Anlatımı
Bu konu, TYT’de temel düzeyde gelirken AYT’de daha çok yorumlama, denklem kurma ve problem çözme ağırlıklı karşımıza çıkar. Özellikle geometri, problemler, denklem sistemleri ve fonksiyonlar gibi alanlarla iç içedir.
📌 1. Oran Nedir?
İki çokluğun birbirine bölünerek karşılaştırılmasına oran denir.
Örnek:
Bir sınıfta 12 kız ve 8 erkek varsa, kızların erkeklere oranı:
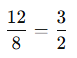
📌 2. Orantı Nedir?
İki oranın birbirine eşit olması durumuna orantı denir.
![]()
📘 Oran – Orantı Ünitesinin Alt Başlıkları:
-
Temel Kavramlar: Oran ve Orantı Tanımı
-
Doğru Orantı
-
Ters Orantı
-
Karışık Orantı
-
Oran-Orantı Problemleri
-
AYT Düzeyinde Uygulama Soruları
🎯 AYT’de Oran – Orantı Nasıl Sorulur?
-
Denklem kurma
-
Doğru/ters orantı yorumlama
-
Kesirli – rasyonel ifadelerle denklem
-
Sayı problemleri içinde orantı kullanımı
-
Grafik yorumlama içinde oran ilişkisi
-
Geometrik oranlarla (uzunluk, alan, hacim) karışık sorular
🎓 Basit Örnek:
Soru:
a ile b doğru orantılı, a = 6 iken b = 9 ise, a = 10 iken b kaç olur?
Çözüm:

Oran ve Orantı Tanımı ve Özellikleri
Bu başlık, ünitenin temelini oluşturur. Özellikle AYT sorularında karşılaştırma, denklem kurma ve mantık yürütme için bu kavramların net anlaşılması şarttır.
📘 A. Oran Nedir?
İki çokluğun birbirine bölünerek karşılaştırılmasıdır.
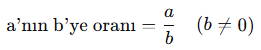
Oranlar birim içermez, yani “saf sayılardır.”
🎓 Örnek 1:
Bir sınıfta 15 kız ve 10 erkek öğrenci var.
Kızların erkeklere oranı:
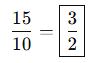
🎓 Örnek 2:
Bir karışımda 2 litre su ve 3 litre sirke varsa, su/sirke oranı:
![]()
📘 B. Orantı Nedir?
İki oranın birbirine eşit olması durumudur.
📌 Özellik: Çapraz Çarpım
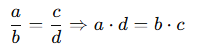
Bu özellik, orantı kurulan tüm sorularda kullanılabilir.
🎓 Örnek 3:
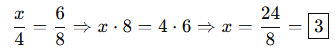
📘 Oran ve Orantının Bazı Özellikleri:
-
Oranlarda sadeleştirme yapılabilir.
-
Orantıda benzer oranlar eşit kabul edilir.
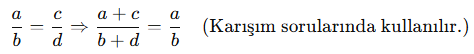
-
Orantı içeren denklemlerde bilinmeyen bulunabilir.
Uygulamalı Mini Alıştırmalar:
Soru 1:
a : b = 3 : 5 ve b : c = 10 : 7 ise, a : b : c oranı nedir?
Çözüm:
-
b’yi eşitleyelim:
İlk oranda b = 5, ikinci oranda b = 10 → 2 katla:
a : b = 6 : 10, b : c = 10 : 7
![]()
Soru 2:
Çözüm:
Çapraz çarpım:
![]()
AYT’de Dikkat Edilecekler:
-
Oran ve orantı karıştırılmamalı: oran ≠ orantı
-
Orantı sorularında çapraz çarpım çoğu zaman anahtardır
-
Sayısal değil, mantıksal ilişki içeren sorular da çıkar
-
Bileşik oran, karışım ve denge soruları bu temele dayanır
Doğru Orantı
📘 Tanım:
İki çokluktan biri artarken diğeri de aynı oranda artıyor, biri azalırken diğeri de aynı oranda azalıyorsa bu iki çokluk doğru orantılıdır.
Matematiksel ifade:
ya da
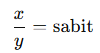
🔹 Özellikler:
-
Grafik çizerseniz, orijin (0,0)’dan geçen doğru bir çizgi elde edilir.
-
Çokluklar birbirine bağlı olarak doğru orantılıysa, biri iki katına çıkarsa diğeri de iki katına çıkar.
-
En çok iş, işçi, saat ve dozaj, karışım, oran hesaplama gibi problemlerde kullanılır.
🎓 Örnek 1:
Bir işçi 6 saatte 12 parça eşya üretiyor.
Aynı hızda çalışan biri 10 saatte kaç parça üretir?
Çözüm:
İşçi süresiyle üretim doğru orantılıdır.
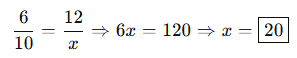
🎓 Örnek 2:
Bir otomobil saatte 60 km hızla 2 saatte 120 km gider.
Aynı yolda saatte 80 km hızla kaç saatte gider?
Çözüm:
Hız arttıkça süre azalır → ters orantı
(Bu örnek aslında ters orantı örneği olurdu, dikkat! Az sonra o başlığa geçeceğiz.)
AYT’de Doğru Orantı Nerede Karşımıza Çıkar?
-
İşlem hızı, üretim, çalışma süresi problemleri
-
Doğrudan denklem kurulabilen oran ilişkileri
-
Özellikle karışım ve oran hesaplama problemlerinde
-
Alan, hacim, uzunluk gibi geometrik büyüklükler arasındaki ilişkilerde
Mini Test
Soru:
Bir musluk, bir havuzu 6 saatte dolduruyorsa aynı debide çalışan 3 musluk birlikte kaç saatte doldurur?
Çözüm:
Musluk sayısı artarsa süre azalır → ters orantı
(Soru ters orantıymış! Ama bu da farkı anlamak için güzel bir geçiş olur.)
Ters Orantı
📘 Tanım:
İki çokluktan biri artarken diğeri azalıyorsa, bu iki çokluk ters orantılıdır.
Matematiksel ifade:
![]()
🔹 Temel Özellikler:
-
Birçok iş-güç, zaman-hız problemi ters orantıya dayanır
-
Grafik olarak hiperbol (eğri) oluşturur
-
Doğru orantının tersidir: biri 2 katına çıkarsa diğeri yarıya iner
🎓 Örnek 1:
Bir işçi bir işi 12 günde bitiriyor.
Aynı hızda çalışan 3 işçi aynı işi kaç günde bitirir?
Çözüm:
İşçi sayısı arttıkça süre azalır → ters orantı:
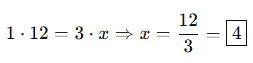
🎓 Örnek 2:
Bir otomobil saatte 60 km hızla bir yolu 4 saatte gidiyor.
Aynı yolu saatte 80 km hızla kaç saatte gider?
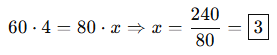
📌 Ters Orantı İfadeleri:
Sorularda şu tarz ifadeler varsa ters orantı olduğunu anlayabilirsin:
-
“Daha fazla kişi → daha az süre”
-
“Hız arttıkça süre azalır”
-
“Güç arttıkça iş süresi kısalır”
-
“Debi artarsa doldurma süresi azalır”
❗ Dikkat:
Eğer birden fazla çokluk varsa (örneğin işçi – iş – zaman gibi), oran kurarken sabit tutulan büyüklüğü doğru anlamak gerekir.
Aksi halde doğru orantı yerine yanlışlıkla ters orantı kurulabilir.
Mini Uygulama Sorusu:
Soru:
5 işçi bir işi 12 günde bitiriyor.
Aynı iş, 3 işçiyle kaç günde biter?
Çözüm:
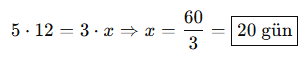
AYT’de Dikkat Edilecekler:
-
İşçi – zaman – iş miktarı türü problemler %90 ters orantıdır
-
Oran kurarken hangi büyüklük sabit kalıyor? (iş mi, yol mu?) mutlaka belirlenmeli
-
Doğru orantı ile ters orantı karıştırılmamalı
-
AYT’de bu tip sorular genellikle kısa ama dikkat isteyen sorular olur
Karışık Orantı (Birleşik Orantı)
📘 Tanım:
Bir büyüklük, birden fazla değişkenle bazılarına doğru, bazılarına ters orantılı olacak şekilde ilişkiliyse buna karışık orantı denir.
🔹 Genel Biçim:
Bir işin süresi:
-
İşçi sayısıyla ters orantılı
-
Günlük çalışma saatiyle ters orantılı
-
Yapılacak iş miktarıyla doğru orantılıdır.
Böylece:

🎯 AYT’de Nasıl Karşımıza Çıkar?
-
İş – işçi – zaman – vardiya gibi karışık tablolar
-
Yol – hız – zaman – araç sayısı problemleri
-
Aynı anda hem artan hem azalan değişkenler varsa
🎓 Örnek 1:
4 işçi günde 6 saat çalışarak bir işi 10 günde bitiriyor.
Aynı işi 6 işçi, günde 5 saat çalışarak kaç günde bitirir?
📌 Çözüm:
İşin süresi (x) işçi ve saatle ters, iş miktarıyla doğru orantılıdır.
Aynı iş yapılıyor → iş miktarı sabit.
Oran kur:
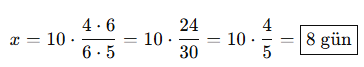
🎓 Örnek 2:
Bir grup işçi, 3 vardiya hâlinde çalışarak 12 günde bir işi tamamlıyor.
İşçi sayısı %50 artırılır, vardiya 2’ye düşürülürse iş kaç günde biter?
📌 Çözüm:
-
İşçi sayısı artışı → süre azalır (ters)
-
Vardiya azalması → süre artar (ters)
Toplam oran:
💡 Oran değişse bile sonuç aynı çıkabilir — sınavlarda dikkat tuzağı olabilir!
Mini Uygulama Sorusu:
Soru:
8 işçi, 9 saat çalışarak 15 günde bir işi bitiriyor.
Aynı işi 6 işçi, 10 saat çalışarak kaç günde bitirir?
Çözüm:
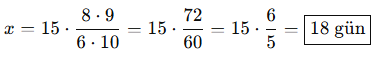
AYT’de Dikkat Edilecekler:
-
“Doğru – ters” ilişkileri önce netleştirilmeli
-
İş miktarı sabitse sadeleşir, değilse hesaba dâhil edilir
-
Yüzdelik değişim varsa oranlara dikkat edilmeli
-
Oranların yerleri karıştırılırsa doğru sonuç vermez
Oran – Orantı Problemleri
Bu bölümde oran ve orantının doğrudan uygulandığı metinli, dikkat isteyen problem türlerini ele alacağız. Sorular genelde:
-
Oranla verilen sayıları bulma
-
Birbirine bağlı çoklukları tanıma
-
Doğru/ters/karışık orantıyı yorumlama
şeklinde karşımıza çıkar.
📘 Soru Türleri ve Örnekler
🎓 Soru 1: Oranı Verilen Sayıları Bulma
Soru:
a : b = 4 : 5 ve a + b = 36 ise, a – b kaçtır?
Çözüm:
-
a = 4k, b = 5k → a + b = 9k = 36 → k = 4
-
a = 16, b = 20 → a – b = −4
🎓 Soru 2: Doğru Orantı ile Problem
Soru:
6 işçi bir işi 8 günde yapıyor. Aynı iş 4 işçiyle kaç günde yapılır?
Çözüm:
İşçi sayısı ile süre ters orantılı:
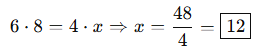
🎓 Soru 3: Sayıların Oranları ile Toplamı Verilen Problem
Soru:
Bir sayının 3 katı ile başka bir sayının 2 katının toplamı 34’tür.
Bu iki sayının oranı 2 : 1 olduğuna göre sayılar kaçtır?
Çözüm:
Orana göre sayıların biri 2k, diğeri k olsun.
K tam sayı çıkmadı → oran yanlış kurulmuş olabilir ya da sayı sorusu değildir.
Bu tarz sorularda sayının türü (tam sayı mı?) mutlaka kontrol edilmeli!
🎓 Soru 4: Karışım Problemi
Soru:
5 litrelik karışımın su/sirke oranı 3:2’dir.
Karışıma 1 litre su eklenirse yeni oran nedir?
Çözüm:
Toplam 5 litre → 3k + 2k = 5k = 5 ⇒ k = 1
-
Su = 3, sirke = 2
-
Yeni su = 3 + 1 = 4 ⇒ oran:
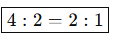
🎓 Soru 5: Eşit Orantılı Sayılar Problemi
Soru:
a : b = b : c = 2 : 3 ise a : c oranı nedir?
Çözüm:
a = 2k, b = 3k
Ama aynı zamanda b : c = 2 : 3 olmalı →
b = 2m, c = 3m ⇒ b ortak ⇒
3k = 2m → k = 2, m = 3 ⇒
a = 2k = 4, c = 3m = 9 ⇒ a : c = ![]()
AYT’de Dikkat Edilecekler:
-
Oran verip toplam soruyorsa → orantı sabitleriyle işlem yap
-
Karışım, işçi, hız problemleri orantının içinde gizlidir
-
Oran – orantı soruları genelde sade görünür ama dikkat tuzağı içerir
-
Oranları mutlaka sayılara çevirerek işle
AYT Düzeyinde Oran – Orantı Soruları
Aşağıda AYT ayarında hazırlanmış 10 soruluk bir deneme testi var. Her soru farklı kazanımları ölçer.
Cevap anahtarı en altta.
📘 AYT – Oran Orantı Mini Deneme (10 Soru)
1.
a : b = 3 : 5 ve a + b = 64 ise, a – b kaçtır?
A) –16
B) –8
C) 8
D) 16
2.
Bir işçi 8 günde 24 parça ürün üretiyor. Aynı hızla çalışan 3 işçi aynı işi kaç günde 108 parça üretir?
A) 9
B) 10
C) 12
D) 8
3.
a : b = 2 : 3 ve b : c = 6 : 5 ise, a : b : c oranı nedir?
A) 4 : 6 : 5
B) 2 : 3 : 5
C) 2 : 3 : 2.5
D) 3 : 6 : 5
4.
Bir karışımın su : şeker oranı 4 : 1’dir. Karışıma 3 litre su eklenince oran 5 : 1 oluyor. Başlangıçta kaç litre karışım vardı?
A) 20 B) 24 C) 25 D) 30
5.
a : b = b : c = 3 : 2 ise, a : c oranı nedir?
A) 3 : 2
B) 3 : 1
C) 9 : 4
D) 2 : 3
6.
x doğru orantılı, y ters orantılıysa:
olduğuna göre, x = 6 iken y kaçtır?
A) 4 B) 3 C) 2 D) 1
7.
Bir grup işçi, günde 8 saat çalışarak 15 günde bir işi bitiriyor. Aynı iş, günde 10 saat çalışacak şekilde 6 işçiyle kaç günde tamamlanır?
A) 10 B) 12 C) 16 D) 18
8.
Aşağıdaki eşitlik doğruysa, x kaçtır?
A) 1 B) 2 C) 3 D) 4
9.
Bir telin 3 : 5 oranında iki parçaya ayrılması isteniyor. Telin uzunluğu 64 cm olduğuna göre, büyük parça kaç cm olur?
A) 35 B) 36 C) 40 D) 45
10.
Bir işçi bir işi 12 günde yapıyor. Aynı iş, %50 daha fazla işçiyle kaç günde yapılır?
A) 6 B) 8 C) 9 D) 10