Sayısal Nicelikler Konu Anlatımı

Matematik, hayatımızın her alanında var olan bir bilimdir. Günlük yaşantımızda alışveriş yaparken, saatleri okurken, yolculuk mesafelerini hesaplarken ve hatta oyun oynarken bile matematiği kullanırız. Bu ünitede, matematiğin temel taşlarından biri olan doğal sayılar ve işlemler konusunu ele alacağız.

Doğal sayılar, 0 ve ondan büyük tüm pozitif tam sayıları kapsar. Bu sayılarla toplama, çıkarma, çarpma ve bölme işlemleri yapılabilir. Ancak, sadece dört işlemle sınırlı değiliz! Sayılar üzerinde çarpanlar ve katları belirleme, bölünebilme kurallarını anlama, örüntüleri keşfetme ve işlem tahmin stratejileri geliştirme gibi birçok önemli matematiksel beceri kazanacağız.

Bu ünite boyunca:
✔ Altı basamaklı sayıları okuma ve yazma becerimizi geliştireceğiz.
✔ Doğal sayılarla işlemler yaparak problem çözme yeteneğimizi artıracağız.
✔ Kesirleri ve farklı gösterimlerini tanıyıp gerçek hayatla ilişkilendireceğiz.
✔ Sayı örüntülerini keşfederek matematiksel kurallar oluşturacağız.
✔ Çarpanlar ve katları kullanarak en büyük ortak bölen (EBOB) ve en küçük ortak katı (EKOK) hesaplayacağız.
✔ Yuvarlama yöntemleriyle işlem sonuçlarını tahmin etmeyi öğreneceğiz.

Matematiği öğrenirken keşfetmek, tahmin etmek ve problem çözmek çok eğlencelidir! Haydi, sayıların dünyasına birlikte adım atalım! 🚀

MAT.5.1.1. Altı Basamaklı Sayıları Okuma ve Yazma

1. Günlük Hayatta Altıdan Çok Basamaklı Sayılar

Matematik, sadece derslerde öğrendiğimiz bir konu değil, hayatımızın her alanında karşımıza çıkar. Altı basamaklı ve daha büyük sayılar, özellikle ekonomi, nüfus bilgileri, spor, astronomi ve bilimsel hesaplamalar gibi alanlarda sıkça kullanılır.

Gerçek Hayattan Örnekler:

• Nüfus Verileri: Ankara’nın nüfusu yaklaşık 5.100.000 kişidir.
• Para Miktarları: Büyük şirketlerin bütçeleri milyonlarca lirayı bulabilir. Örneğin, bir belediyenin yıllık bütçesi 750.482.000 TL olabilir.
• Spor: Bir futbol maçında toplam 65.218 kişi tribünlerde olabilir.
• Uzay: Dünya ile Ay arasındaki mesafe yaklaşık 384.400 kilometredir.

✍ Soru:
Sen de çevrende sıkça kullanılan altı basamaklı veya daha büyük bir sayı örneği bulabilir misin?

2. Sayıların Bölükleri ve Okunuşları

Büyük sayıları okurken zorlanmamak için bölükler kullanılır. Bölük, bir sayının sağdan sola doğru üçlü gruplara ayrılmasını ifade eder.

📌 Bölükler:

1. Birler Bölüğü: 000
2. Binler Bölüğü: 000
3. Milyonlar Bölüğü: 000

📌 Önemli Nokta: Sayıların üçerli gruplar halinde bölükler şeklinde okunması, büyük sayıları anlamayı kolaylaştırır.

📌 Sayıların Okunuşunda Kurallar:
✅ Sayılar bölüklere ayrılarak okunur.
✅ Sayının başında sıfır bulunmaz (Örneğin, 000.245 yerine 245 yazılır).
✅ Birimler belirtilmeden okunmaz (Örneğin, 5.100.000 → Beş milyon yüz bin şeklinde okunmalıdır).

✍ Soru:
Aşağıdaki sayıları bölüklere ayırarak okuyunuz.

1. 768.315
2. 4.502.817
3. 1.083.029

3. Altıdan Çok Basamaklı Sayıları Okuma ve Yazma Kuralları

Altıdan fazla basamağı olan sayılar okunurken ve yazılırken bazı kurallar takip edilmelidir:

1️⃣ Sayılar üçlü gruplara (bölüklere) ayrılmalıdır.
2️⃣ Her bölük arasına nokta konularak yazılmalıdır.
3️⃣ En büyük bölükten başlanarak okunmalıdır.

Örnekler:

✅ 7.234.156 → Yedi milyon iki yüz otuz dört bin yüz elli altı
✅ 16.482.209 → On altı milyon dört yüz seksen iki bin iki yüz dokuz
✅ 205.000.321 → İki yüz beş milyon üç yüz yirmi bir

📌 Özel Durumlar:

• Eğer binler bölüğü 000 ise, bin kelimesi okunmaz.
• Eğer milyonlar bölüğü 000 ise, milyon kelimesi okunmaz.

✍ Soru:
Aşağıdaki sayıların doğru okunuşlarını yazınız.

1. 98.756.432
2. 125.004.918
3. 7.030.120

4. Sayıların Bölükleri ile Okunuşları Arasındaki Ortak Özellikler

Bölükler arasındaki örüntüleri fark etmek, sayıları okumayı ve yazmayı kolaylaştırır.
Ortak Özellikler:

• Her bölük üç basamaktan oluşur.
• Bir bölük tamamlandığında diğerine geçilir.
• Sayılar sağdan sola üçerli ayrıldığında aynı yapıyı tekrar eder.

🟢 Örnek:
Sayı: 476.285.932
Bölüklere ayırma: 476 285 932
Okunuşu: Dört yüz yetmiş altı milyon iki yüz seksen beş bin dokuz yüz otuz iki

✍ Soru:
Sen de benzer bir örnek oluştur ve bölüklere ayırarak yaz!

5. Altıdan Çok Basamaklı Sayıların Okunuş ve Yazılışı Hakkında Önerme Geliştirme

Bir sayının basamak sayısı altıdan fazla olduğunda bazı örüntüler ortaya çıkar:

✅ Her üç basamak bir bölük oluşturur.
✅ En sağdan başlayarak üçlü gruplar oluşturulur.
✅ Okuma ve yazma işlemi en büyük bölükten en küçüğe doğru yapılır.

📌 Önerme Örnekleri:

• Eğer bir sayının milyonlar bölüğü sıfır değilse, o sayı milyonlu bir sayıdır.
• Eğer binler bölüğü sıfır ise, “bin” kelimesi kullanılmaz.
• Eğer bütün rakamlar sıfırsa, sayı “sıfır” olarak okunur.

✍ Soru:
Bu kurallara dayanarak 345.000.827 sayısının nasıl okunacağını tahmin ediniz.

Ünite Sonu Etkinliği (Örnek Sorular)

1) Aşağıdaki sayıları bölüklere ayırarak okuyunuz.
a) 52.814.276
b) 7.035.120
c) 125.010.409

2) Aşağıdaki okunuşlara karşılık gelen sayıları yazınız.
a) İki yüz kırk yedi milyon üç yüz sekiz bin yüz yirmi üç
b) Yetmiş sekiz milyon iki yüz on beş bin dokuz yüz elli sekiz

3) Hangi sayının milyonlar basamağı 6’dır?
a) 6.215.489
b) 2.654.321
c) 9.602.741

5.1.2. Doğal Sayılar ve İşlemler İçeren Gerçek Yaşam Problemleri

1. Problemin İçerdiği Sayı ve İşlem Bileşenlerini Belirleme

Matematikte problemleri çözerken öncelikle verilenleri ve istenenleri belirlemek gerekir.
Bir problemde hangi işlemler yapılacağını belirlemek için aşağıdaki soruları sorabiliriz:

✅ Problemde hangi sayılar verilmiş?
✅ Problemde hangi işlemler isteniyor? (Toplama, çıkarma, çarpma, bölme)
✅ Problemi çözmek için hangi bilgileri kullanmalıyız?

📌 Örnek:
Bir okulun kütüphanesinde 3.250 kitap vardır. Okul, kütüphanesine 1.750 yeni kitap ekledi. Kütüphanede toplam kaç kitap oldu?

📌 Çözüm:
Verilenler: 3.250 kitap, 1.750 yeni kitap
İstenen: Toplam kitap sayısı
İşlem: Toplama işlemi
Çözüm: 3.250 + 1.750 = 5.000 kitap

✍ Etkinlik:
Aşağıdaki problemlerde verilenleri ve istenenleri belirleyin.

1. Bir çiftlikte 2.375 tavuk, 3.628 ördek ve 1.829 kaz var. Çiftlikte toplam kaç hayvan var?
2. Bir otomobil fabrikası bir günde 7.280 araba üretiyor. 5 günde toplam kaç araba üretmiş olur?

2. Problemde Verilenler ile İstenenler Arasındaki İlişkiyi Belirleme

Bazen problemler birden fazla işlem gerektirebilir. Böyle durumlarda öncelikle hangi işlemin yapılması gerektiğini belirlemeliyiz.

📌 Örnek:
Bir mağazada önce 2.560 TL değerinde ürün satıldı. Daha sonra mağazaya 4.320 TL’lik yeni ürün eklendi. Mağazada şu an toplam kaç TL’lik ürün var?

Çözüm:

• Önce mevcut miktar bulunur: 2.560 TL
• Yeni eklenen ürün miktarı ile toplanır:
  2.560 + 4.320 = 6.880 TL

✍ Etkinlik:
Aşağıdaki problemlerin çözümünde hangi işlemlerin gerektiğini belirleyin.

1. Bir fabrikada sabah 3.250 adet ekmek üretildi, öğleden sonra 2.900 adet daha üretildi. Günlük toplam üretim kaç ekmek oldu?
2. Bir spor salonunda toplam 8.750 kişi üye. Bunların 4.225’i erkek. Kaç üye kadındır?

3. Problemdeki Verilenleri Matematiksel Temsillere Dönüştürme

Bazı problemler sözel olarak verilir. Matematiksel ifadeye dönüştürmek, çözümü kolaylaştırır.

📌 Örnek:
Bir otobüs firmasının 5 otobüsü var. Her otobüste 42 yolcu taşınıyor. Firma, günlük olarak toplam kaç yolcu taşıyor?

Matematiksel ifade:
5 × 42 = ?
Çözüm: 5 × 42 = 210 yolcu

✍ Etkinlik:
Aşağıdaki sözel ifadeleri matematiksel ifadelere dönüştürün.

1. Bir çiftçi, her biri 26 kg olan 9 çuval buğday aldı. Çiftçinin toplam kaç kg buğdayı oldu?
2. Bir kitapçı, 4 gün boyunca her gün 275 kitap satıyor. 4 günde toplam kaç kitap satılmış olur?

4. Problemi Matematiksel Temsiller Kullanarak Açıklama

Bazı problemleri çözmeden önce tahmin yapmak, işlem doğruluğunu kontrol etmeye yardımcı olur.
Örneğin, “500’den biraz büyük bir sonuç çıkabilir mi?” gibi tahminler, sonucu kontrol etmemize yardımcı olur.

📌 Örnek:
Bir okulda 368 kız öğrenci, 412 erkek öğrenci vardır. Okulun toplam öğrenci sayısını tahmin edin.

Çözüm:
368 + 412 ≈ 800 öğrenci (Kesin sonuç: 780)

✍ Etkinlik:
Aşağıdaki işlemleri tahmin ederek yaklaşık sonucu belirleyin.

1. 4.750 + 2.860 ≈ ?
2. 3.625 – 1.895 ≈ ?

5. Problemin Sonucuna Tahmin Yürütme ve Strateji Geliştirme

Problem çözmek için farklı stratejiler geliştirmek gerekir.
Bazı yaygın problem çözme stratejileri şunlardır:

✅ Tahmin yap ve kontrol et
✅ Çizerek göster
✅ Bir tablo oluştur
✅ Kendi sözcüklerinle anlat
✅ Örüntüyü fark et ve genelleştir

📌 Örnek:
Bir kitapçı her ay 3.250 TL kazanç sağlıyor. 12 ay sonra toplam kazancı tahmin edin.

Tahmini Çözüm:
3.000 × 12 = 36.000 TL
Kesin Çözüm: 3.250 × 12 = 39.000 TL

✍ Etkinlik:
Aşağıdaki problemlere uygun bir strateji belirleyin ve çözümünü açıklayın.

1. Bir market her gün 1.175 ekmek satıyor. Bir haftada kaç ekmek satılmış olur?
2. Bir belediye 8.520 kişi kapasiteli bir stadyum inşa ediyor. 4 tane böyle stadyum inşa ederse toplam kaç kişilik kapasite olur?

5.1.3. Gerçek Yaşam Durumlarına Karşılık Gelen Kesirler

1. Kesirlerin Gerçek Yaşamda Kullanımı

Kesirler, günlük hayatta birçok yerde karşımıza çıkar. Örneğin:
✅ Pizza dilimleri kesirlerle ifade edilir. (Yarım pizza, çeyrek dilim vb.)
✅ Saatler kesirlerle ifade edilir. (Saatin dörtte biri, yarısı gibi)
✅ İndirimler yüzdelik kesirlerle gösterilir. (%50 indirim, %25 kar payı gibi)
✅ Sıvı ölçüleri kesirlerle kullanılır. (1/2 litre su, 3/4 bardak süt gibi)

Örnekler: Kesirler ve Gerçek Yaşam İlişkisi

Örnek 1: Pizza Dilimleri
Bir pizzayı 8 dilime böldüğümüzde, 3 dilim yediğimizde kalan kısmı kesirle nasıl ifade ederiz?

📌 Çözüm:

• Pizzanın tamamı 8/8’dir.
• 3 dilim yediğimizde kalan dilimler 5/8 olur.

Örnek 2: İndirim Oranları
Bir mağazada tüm ürünlerde %25 indirim var. Bu oran kesirle nasıl ifade edilir?

📌 Çözüm:

• %25 = 25/100 = 1/4
  Yani her 4 birimlik fiyattan 1 birim indirim yapılır.

Örnek 3: Sıvı Ölçüleri
Bir sürahide 4 litre su var. Bunun 3/4’ü bardağa dökülürse kaç litre su dökülmüş olur?

📌 Çözüm:

• 4 × 3/4 = 3 litre su bardağa dökülmüş olur.

✍ Etkinlik:

1. Bir çikolata 10 parçaya bölündü. 6 parçasını yersen geriye kalan kısmı kesirle nasıl ifade edersin?
2. Bir okulda 300 öğrenci var. Bunların 1/5’i basketbol takımına seçildi. Kaç öğrenci basketbol takımına seçildi?

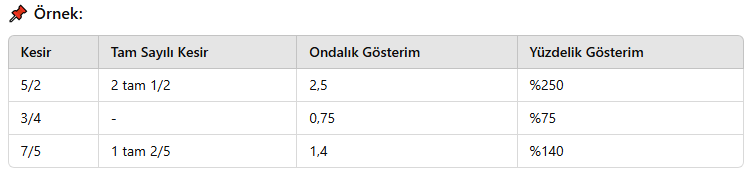
2. Kesirlerin Farklı Gösterimleri (Bileşik, Tam Sayılı, Ondalık ve Yüzdelik Kesirler)

Kesirler farklı biçimlerde gösterilebilir. Bunlar:

✅ Basit Kesirler: Payı paydasından küçük olan kesirlerdir. (Örn: 3/5, 2/7)
✅ Bileşik Kesirler: Payı paydasına eşit veya büyük olan kesirlerdir. (Örn: 7/4, 9/3)
✅ Tam Sayılı Kesirler: Bileşik kesirlerin tam sayı ve kesir kısmı ayrılarak yazılmasıdır. (Örn: 2 tam 1/3)
✅ Ondalık Gösterim: Kesirlerin ondalık sistemde yazılmasıdır. (Örn: 1/2 = 0,5)
✅ Yüzdelik Kesirler: Kesirlerin % sembolüyle gösterilmesidir. (Örn: 1/4 = %25)

✍ Etkinlik:

1. 2/5, 5/8 ve 7/3 kesirlerini ondalık ve yüzdelik gösterime çevirin.
2. 11/4 kesirini tam sayılı kesir olarak yazınız.

3. Gerçek Yaşam Kesirlerini Modellerle İlişkilendirme

Kesirleri anlamanın en iyi yolu modeller kullanmaktır.
Kesir modelleri:

• Şekil modelleri (çember, kare vb.)
• Sayı doğrusu
• Somut nesneler (çubuklar, paralar, ölçü kapları vb.)

📌 Örnek:
Bir sayfa 4 eşit parçaya bölündü. 3 parçası boyandı. Kesir modeliyle gösterelim:

🟩🟩🟩⬜ → 3/4 (Üç bölü dört boyanmış)

📌 Sayı Doğrusu Örneği:

Burada 3/4, 1 tamın biraz gerisinde yer alır.

✍ Etkinlik:

1. 1/3 ve 2/5 kesirlerini sayı doğrusu üzerinde gösterin.
2. 5/8 kesrini bir çember modeliyle çizin.

4. Kesirlerin Farklı Temsilleri ile Karşılaştırılması

Farklı temsillerle ifade edilen kesirler birbirine eşdeğer olabilir veya farklı büyüklükte olabilir.

📌 Örnek:
1/2, 2/4 ve 3/6 kesirleri eşdeğerdir, çünkü hepsi yarımı temsil eder.

Kesir Karşılaştırma Yöntemleri:
✅ Paydaları eşitleme yöntemi
✅ Ondalık gösterime çevirme
✅ Modellerle gösterme

📌 Örnek:
Hangi kesir büyüktür? 3/5 mi, 2/3 mü?

• Ortak payda bulunur: 3/5 = 9/15, 2/3 = 10/15
• 10/15 > 9/15 olduğundan, 2/3 daha büyüktür.

✍ Etkinlik:

1. 4/7 mi büyüktür, yoksa 5/8 mi?
2. 3/5 ve 6/10 kesirlerinin eşit olup olmadığını açıklayın.

5.1.4. Farklı Gösterimlerle İfade Edilen Kesirlerin Karşılaştırılması

1. Kesirlerin Karşılaştırılmasında Kullanılan Yöntemler

Bir kesrin diğerinden büyük ya da küçük olup olmadığını belirlemek için farklı yöntemler kullanabiliriz:

✅ Paydaları Eşitleme Yöntemi
✅ Ondalık Gösterime Çevirme Yöntemi
✅ Model Kullanma Yöntemi
✅ Sayı Doğrusu Üzerinde Gösterme Yöntemi

Öğrenciler, bu yöntemleri kullanarak kesirleri sıralayabilir ve karşılaştırabilir.

2. Paydaları Eşitleyerek Kesir Karşılaştırma

Kesirleri karşılaştırırken paydalar aynı değilse, önce eşit paydalara getirilmelidir.

📌 Örnek:
Hangisi daha büyüktür? 3/5 mi, 2/3 mü?

1️⃣ Ortak payda bulunur:

• 5 ve 3’ün ortak katı 15’tir.
• 3/5 = 9/15, 2/3 = 10/15

2️⃣ Karşılaştırma yapılır:

• 10/15 > 9/15, bu yüzden 2/3 > 3/5

✍ Etkinlik:

1. 4/7 mi büyüktür, yoksa 5/8 mi?
2. 3/4 ve 5/6 kesirlerini karşılaştırın.

3. Kesirleri Ondalık Sayılara Çevirerek Karşılaştırma

Bazı kesirleri ondalık gösterime çevirerek karşılaştırmak daha kolaydır. Bunun için:

• Paydası 10, 100 veya 1000 olacak şekilde genişletilir.
• Bölme işlemi yapılarak ondalık sayı bulunur.

📌 Örnek:
Hangi kesir daha büyüktür? 3/8 mi, 5/12 mi?

1️⃣ 3 ÷ 8 = 0,375
2️⃣ 5 ÷ 12 = 0,416
3️⃣ 0,416 > 0,375 olduğu için 5/12 daha büyüktür.

✍ Etkinlik:

1. 2/5 ve 3/8 kesirlerini ondalık sayıya çevirerek karşılaştırın.
2. 4/9 ve 5/11 kesirlerini karşılaştırın.

4. Kesirleri Sayı Doğrusu Üzerinde Göstererek Karşılaştırma

Kesirleri karşılaştırmanın görsel yollarından biri de sayı doğrusu kullanmaktır. Büyük olan kesir, sayı doğrusunda daha sağda yer alır.

✍ Etkinlik:

1. 1/4, 2/5 ve 3/6 kesirlerini sayı doğrusu üzerinde gösterin.
2. 5/9 ve 3/7 kesirlerinin sayı doğrusu üzerindeki yerini belirleyin.

5. Farklı Gösterimlere Sahip Kesirleri Karşılaştırma

Bazı kesirler farklı biçimlerde gösterilebilir. Örneğin:

✅ Basit Kesir: 3/4
✅ Bileşik Kesir: 7/5
✅ Tam Sayılı Kesir: 1 tam 2/5
✅ Ondalık Gösterim: 0,75
✅ Yüzdelik Gösterim: %75

📌 Örnek:
Hangi daha büyüktür? 2/3 mü, %60 mı?

1️⃣ 2/3’ü yüzde olarak yazalım:
2 ÷ 3 = 0,6667 → %66,67

2️⃣ %66,67 > %60 olduğu için 2/3 daha büyüktür.

✍ Etkinlik:

1. 7/10 mu büyüktür, yoksa %68 mi?
2. 4/9 ve 0,45’i karşılaştırın.

6. Eşdeğer Kesirler

Bazı kesirler farklı yazılsa bile aynı büyüklüğe sahiptir.

📌 Örnek:
1/2 = 2/4 = 4/8 = 0,5 = %50

✍ Etkinlik:

1. 3/6, 2/4 ve 5/10 kesirlerinin eşdeğer olup olmadığını inceleyin.
2. 1/5’i 2 farklı şekilde eşdeğer kesir olarak yazın.

5.1.5. Doğal Sayılarla Çarpma ve Bölme İşlemi

1. Çarpma İşlemi ve Anlamı

Çarpma işlemi, bir sayıyı belirli bir kez toplamak yerine daha kısa bir yolla hesaplama yapmamızı sağlayan işlemdir.

📌 Örnek:
Bir kasada 6 sıra halinde 8 yumurta bulunmaktadır. Toplam kaç yumurta vardır?

✅ Toplama yöntemiyle:
8 + 8 + 8 + 8 + 8 + 8 = 48

✅ Çarpma yöntemiyle:
6 × 8 = 48 yumurta

📌 Çarpmanın Özellikleri:
✅ Değişme (Yer Değiştirme) Özelliği: 4 × 6 = 6 × 4
✅ Birleşme Özelliği: (3 × 4) × 2 = 3 × (4 × 2)
✅ Etkisiz Eleman: 5 × 1 = 5
✅ Sıfır Etkisi: 9 × 0 = 0

✍ Etkinlik:

1. 7 × 9 işleminin sonucunu yazın.
2. Çarpma işleminin özelliklerine uygun 3 örnek verin.

2. Büyük Sayılarla Çarpma İşlemi

Büyük sayılarla çarpma yaparken basamaklara ayırarak işlem yapmak daha kolay olabilir.

📌 Örnek:
452 × 23 işlemini adım adım çözelim:

✅ Önce birler basamağı ile çarpalım:
452 × 3 = 1.356

✅ Şimdi onlar basamağı ile çarpalım (20 yerine 2 ile çarpıp 10 ile genişletiyoruz):
452 × 2 = 904 (Sonra bu sonucu 10 ile çarpıyoruz: 9.040)

✅ Toplayalım:
1.356 + 9.040 = 10.396

✍ Etkinlik:

1. 624 × 35 işlemini adım adım çözün.
2. 7.458 × 42 işleminin sonucunu bulun.

3. Bölme İşlemi ve Anlamı

Bölme işlemi, bir sayıyı eşit parçalara ayırmak veya gruplar oluşturmak için kullanılır.

📌 Örnek:
48 tane kurabiye, 8 çocuğa eşit şekilde dağıtılacaktır. Her çocuk kaç kurabiye alır?

✅ Çözüm:
48 ÷ 8 = 6 kurabiye

📌 Bölmenin Özellikleri:
✅ Bölme işleminin etkisiz elemanı yoktur.
✅ Bölme işleminde sıfırın etkisi:

• Bir sayıyı 0’a bölemezsin! (Tanımsızdır)
• 0’ı herhangi bir sayıya bölersen sonuç 0’dır. (0 ÷ 5 = 0)
  ✅ Bölme işleminde kalan olabilir:
• 37 ÷ 5 = 7 kalan 2

✍ Etkinlik:

1. 84 ÷ 7 işlemini yapın.
2. Bir sayıyı sıfıra bölmek neden tanımsızdır? Açıklayın.

4. Kalanlı Bölme İşlemi

Bazı bölme işlemlerinde bölünen, bölenin tam katı olmadığında kalıntı (kalan) olur.

📌 Örnek:
Bir kutuya her biri 7 kg olan çuvallardan 43 kg sığmaktadır. Bu durumda kaç çuval tam sığar ve ne kadar yer kalır?

✅ Çözüm:
43 ÷ 7 = 6 tam, kalan 1 kg

✍ Etkinlik:

1. 52 ÷ 6 işlemini yaparak bölümü ve kalanı bulun.
2. Bir markette 91 elma, 4’erli kaselere konulacaktır. Kaç kase dolar ve kaç elma dışarıda kalır?

5. Çarpma ve Bölme İşlemlerini Gerçek Hayat Problemlerinde Kullanma

Çarpma ve bölme işlemleri günlük hayatta sıkça kullanılır.

📌 Örnek 1:
Bir öğrenci her gün 4 sayfa kitap okuyor. Bir haftada kaç sayfa okumuş olur?

✅ Çözüm:
4 × 7 = 28 sayfa

📌 Örnek 2:
Bir çiftlikte 168 tavuk, 6 kümese eşit sayıda yerleştiriliyor. Her kümeste kaç tavuk olur?

✅ Çözüm:
168 ÷ 6 = 28 tavuk

✍ Etkinlik:

1. Bir fabrikada her gün 1250 kalem üretiliyor. 30 günde kaç kalem üretilir?
2. Bir kafede 240 bardak çay, 12 masaya eşit şekilde dağıtılıyor. Her masaya kaç bardak çay düşer?

6. İşlem Önceliği: Çarpma ve Bölmenin Toplama ve Çıkarma ile Kullanımı

Matematikte işlemleri doğru sırayla yapmak çok önemlidir. İşlem sırası şu şekildedir:

1️⃣ Önce parantez içindeki işlemler yapılır.
2️⃣ Çarpma ve bölme işlemleri soldan sağa yapılır.
3️⃣ Son olarak toplama ve çıkarma işlemleri yapılır.

📌 Örnek:
24 + 6 × 3 – 8 ÷ 4 = ?

✅ Önce çarpma ve bölme:
6 × 3 = 18
8 ÷ 4 = 2

✅ Şimdi toplama ve çıkarma:
24 + 18 – 2 = 40

✍ Etkinlik:

1. 12 + 4 × 5 – 10 ÷ 2 işlemini yapın.
2. Bir problem oluşturun ve işlem sırasına uygun şekilde çözün.

5.1.6. Doğal Sayılarla İşlem Yaparken Tahmin Stratejileri

1. Tahmin Yapmanın Önemi

Matematikte işlemleri yapmadan önce tahmin yürütmek, hem işlem sonucunun doğruluğunu kontrol etmeye hem de işlemleri zihinden hızlıca yapmaya yardımcı olur.

📌 Tahmin yapmanın faydaları:
✅ Zihinden işlem becerisi kazandırır.
✅ İşlem hatalarını fark etmeyi kolaylaştırır.
✅ Gerçek hayat problemlerinde yaklaşık hesap yapmayı sağlar.

Örneğin:
📌 237 + 482 işleminin sonucunu tahmin edelim.
✅ 237’yi 240’a, 482’yi 480’e yuvarlayalım.
✅ 240 + 480 = 720 (Yaklaşık sonuç)

✍ Etkinlik:

1. 367 + 593 işlemini yaklaşık olarak tahmin edin.
2. 184 × 9 işleminin sonucunu tahmin ederek belirleyin.

2. Yuvarlama Yöntemi ile Tahmin Yapma

İşlem öncesinde sayıları en yakın onluğa, yüzlüğe veya binliğe yuvarlayarak tahmin yapmak mümkündür.

📌 Örnek:
753 + 198 işlemini yuvarlayarak tahmin edelim.
✅ 753 → 750, 198 → 200
✅ 750 + 200 = 950 (Yaklaşık sonuç)

📌 Örnek:
4.279 – 2.146 işlemini yuvarlayarak tahmin edelim.
✅ 4.279 → 4.300, 2.146 → 2.100
✅ 4.300 – 2.100 = 2.200 (Yaklaşık sonuç)

✍ Etkinlik:

1. 6.382 – 1.987 işlemini yuvarlayarak tahmin edin.
2. 845 × 7 işleminin tahmini sonucunu bulun.

3. Zihinden Tahmin Stratejileri

Zihinden işlem yaparken farklı stratejiler kullanılabilir:

✅ Üstten veya alttan yuvarlama
✅ Yakın değerler ekleyerek tahmin yapma
✅ Çarpma işlemlerinde sayı gruplama yöntemi

📌 Örnek:
29 × 8 işleminin sonucunu tahmin edelim.
✅ 29’u 30’a yuvarlayalım.
✅ 30 × 8 = 240 (Yaklaşık sonuç)

📌 Örnek:
148 ÷ 7 işleminin sonucunu tahmin edelim.
✅ 148’i 150’ye yuvarlayalım.
✅ 150 ÷ 7 ≈ 21 (Yaklaşık sonuç)

✍ Etkinlik:

1. 19 × 6 işlemini zihinden tahmin edin.
2. 312 ÷ 9 işlemini tahmini olarak hesaplayın.

4. İşlem Sonucunu Kontrol Etmek için Tahmin Kullanma

İşlem yaptıktan sonra sonucu kontrol etmek için tahmin kullanılabilir.

📌 Örnek:
325 + 478 işlemini yaptık ve 803 sonucunu bulduk. Doğru mu?

✅ Önce tahmin yapalım:
✅ 325 → 300, 478 → 500
✅ 300 + 500 = 800 (Yaklaşık sonuç)
✅ Bulduğumuz 803 sonucu 800’e yakın olduğundan doğru olabilir.

✍ Etkinlik:

1. 846 – 392 işlemini yapın ve sonucunu tahminle kontrol edin.
2. 225 × 4 işlemini hesaplayın ve yaklaşık sonucu karşılaştırın.

5. Gerçek Yaşam Problemlerinde Tahmin Yapma

Tahmin yapma becerisi alışveriş yaparken, para hesaplamalarında, yolculuk süresi tahminlerinde vb. birçok durumda işe yarar.

📌 Örnek:
Bir kitapçıda bir kitabın fiyatı 47 TL’dir. Bir kişi 9 kitap almak isterse yaklaşık ne kadar öder?

✅ 47’yi 50’ye yuvarlayalım.
✅ 50 × 9 = 450 TL (Yaklaşık sonuç)

✍ Etkinlik:

1. Bir markette 29 TL olan bir üründen 6 tane alınırsa yaklaşık kaç TL ödenir?
2. Bir öğrenci her gün ortalama 38 soru çözüyor. Bir haftada yaklaşık kaç soru çözer?

5.1.7. En Yakın Onluk ve Yüzlüğe Yuvarlama

1. Yuvarlama Nedir ve Neden Önemlidir?

📌 Yuvarlama, bir sayıyı kendisine en yakın belirli bir değere getirme işlemidir.
📌 Yuvarlamanın amacı, işlemleri kolaylaştırmak ve tahmini hesaplamaları hızlandırmaktır.
📌 Günlük hayatta alışveriş, ölçüm, nüfus sayımı gibi birçok alanda kullanılır.

📌 Örnek:

• 239 TL’lik bir ürünün fiyatını tahmini hesaplamak için en yakın 10 TL’ye yuvarlayabiliriz.
• Bir okulun 786 öğrencisi varsa yaklaşık öğrenci sayısı 800 olarak ifade edilebilir.

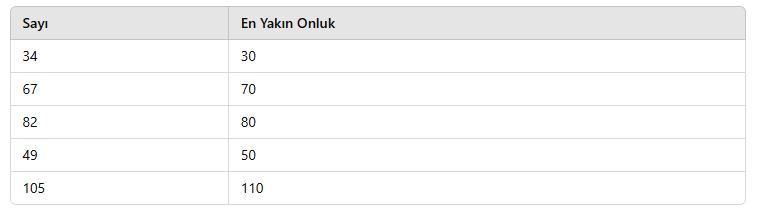
2. En Yakın Onluğa Yuvarlama

Bir sayıyı en yakın onluğa yuvarlamak için birler basamağına bakılır:

✅ 0, 1, 2, 3, 4 → Aşağı yuvarlanır
✅ 5, 6, 7, 8, 9 → Yukarı yuvarlanır

📌 Örnekler:

📌 Örnek:
156 sayısını en yakın onluğa yuvarlayalım:
✅ Birler basamağı 6 olduğu için yukarı yuvarlanır.
✅ Sonuç: 160

✍ Etkinlik:

1. 78, 142, 365 ve 997 sayılarının en yakın onluklarını bulun.
2. Hangi sayılar 50’ye yuvarlanır?

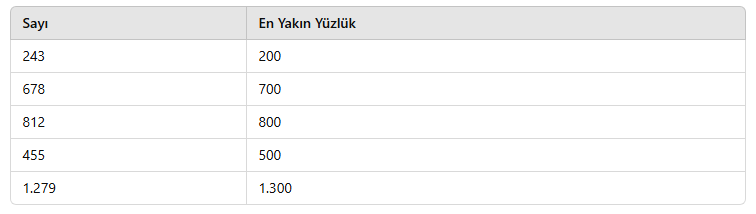
3. En Yakın Yüzlüğe Yuvarlama

Bir sayıyı en yakın yüzlüğe yuvarlamak için onlar basamağına bakılır:

✅ 0, 1, 2, 3, 4 → Aşağı yuvarlanır
✅ 5, 6, 7, 8, 9 → Yukarı yuvarlanır

📌 Örnekler:

📌 Örnek:
738 sayısını en yakın yüzlüğe yuvarlayalım:
✅ Onlar basamağı 3 olduğu için aşağı yuvarlanır.
✅ Sonuç: 700

✍ Etkinlik:

1. 489, 765, 1.234 ve 2.899 sayılarının en yakın yüzlüklerini bulun.
2. Hangi sayılar 600’e yuvarlanır?

4. Gerçek Hayatta Yuvarlama Kullanımı

📌 Örnek 1:
Bir şehirde 2.843.721 kişi yaşıyor. Yaklaşık nüfusu söylemek için en yakın yüz bine yuvarlayalım.
✅ 2.843.721 → 2.800.000 (Yaklaşık nüfus)

📌 Örnek 2:
Bir mağazada 459 TL değerinde bir ürün var. Yaklaşık fiyatı hesaplamak için en yakın yüzlüğe yuvarlayalım.
✅ 459 → 500 TL

✍ Etkinlik:

1. 4.679 kişilik bir stadın kapasitesini yaklaşık hesaplayın.
2. Bir markette 1.278 adet ürün vardır. Yaklaşık kaç ürün olduğu söylenebilir?

5. Yuvarlama Yaparak İşlem Sonucunu Tahmin Etme

Toplama ve çıkarma işlemleri yaparken sayıları yuvarlayarak tahmin yapmak mümkündür.

📌 Örnek:
487 + 319 işlemini tahmini olarak hesaplayalım:
✅ 487 → 490, 319 → 320
✅ 490 + 320 = 810 (Yaklaşık sonuç)

📌 Örnek:
1.238 – 672 işlemini yuvarlayarak tahmin edelim:
✅ 1.238 → 1.200, 672 → 700
✅ 1.200 – 700 = 500 (Yaklaşık sonuç)

✍ Etkinlik:

1. 678 + 842 işlemini en yakın yüzlüğe yuvarlayarak tahmin edin.
2. 1.987 – 1.102 işlemini en yakın yüzlüğe yuvarlayarak hesaplayın.

5.1.8. Sayı Örüntüleri ve Kural Bulma

1. Örüntü Nedir?

📌 Örüntü, belirli bir kurala göre tekrarlayan veya artan-azalan bir dizidir.

Örüntüler günlük hayatta birçok yerde görülür:
✅ Zaman (haftanın günleri, aylar, saatler)
✅ Matematik (çarpım tablosu, ardışık sayılar)
✅ Doğa (çiçek yapraklarının dizilimi, kar tanesi desenleri)

📌 Örnek:
2, 4, 6, 8, 10, …
✅ Her sayı bir öncekinin 2 fazlasıdır.
✅ Örüntü kuralı: “Bir önceki sayıya 2 ekle.”

✍ Etkinlik:

1. 5, 10, 15, 20, … örüntüsünün kuralını bulun.
2. 3, 6, 9, 12, … örüntüsünün bir sonraki üç terimini yazın.

2. Sayısal Örüntülerin Kuralını Belirleme

Sayısal örüntüler artış veya azalış kurallarına göre ilerler.

📌 Örnek:
1, 4, 9, 16, 25, …
✅ Bu örüntünün kuralı: “Her sayı, bir doğal sayının karesidir.”
✅ 1², 2², 3², 4², 5², …

📌 Örnek:
81, 72, 63, 54, …
✅ Her sayı 9 azalarak devam ediyor.
✅ Örüntü kuralı: “Bir önceki sayıdan 9 çıkar.”

✍ Etkinlik:

1. 2, 5, 10, 17, 26, … örüntüsünün kuralını bulun.
2. 48, 44, 40, 36, … örüntüsünün kuralını ve sonraki iki terimini yazın.

3. Örüntüyü Genişletme (Sonraki Terimleri Bulma)

Bir örüntüde kuralı belirledikten sonra, sıradaki sayıları bulabiliriz.

📌 Örnek:
7, 14, 21, 28, …
✅ Örüntü kuralı: “Her sayıyı 7 artır.”
✅ Bir sonraki üç terim: 35, 42, 49

✍ Etkinlik:

1. 4, 9, 14, 19, 24, … örüntüsünü 3 terim genişletin.
2. 64, 32, 16, 8, … örüntüsünün sonraki iki terimini yazın.

4. Sayı Örüntülerinde Eksik Sayıyı Bulma

Bazı örüntülerde eksik sayılar verilir ve kurala göre doldurulması istenir.

📌 Örnek:
3, 6, __, 12, 15, __, 21
✅ Örüntü kuralı: “Her sayıya 3 ekle.”
✅ Eksik sayılar: 9 ve 18

📌 Örnek:
100, __, 80, __, 60, __, 40
✅ Örüntü kuralı: “Her sayıdan 10 çıkar.”
✅ Eksik sayılar: 90, 70, 50

✍ Etkinlik:

1. 2, __, 8, 11, __, 17, 20 örüntüsündeki eksik sayıları tamamlayın.
2. 144, __, 72, __, 18, __, 9 örüntüsünün eksik sayılarını bulun.

5. Çarpma ve Bölme ile Oluşan Örüntüler

Örüntüler yalnızca toplama ve çıkarma ile değil, çarpma ve bölme işlemleriyle de oluşturulabilir.

📌 Örnek:
3, 6, 12, 24, 48, …
✅ Örüntü kuralı: “Her sayıyı 2 ile çarp.”
✅ Sonraki üç terim: 96, 192, 384

📌 Örnek:
512, 256, 128, 64, 32, …
✅ Örüntü kuralı: “Her sayıyı 2’ye böl.”
✅ Sonraki iki terim: 16, 8

✍ Etkinlik:

1. 5, 10, 20, 40, 80, … örüntüsünün kuralını belirleyin.
2. 729, 243, 81, 27, … örüntüsünün sonraki iki terimini bulun.

6. Örüntüleri Gerçek Yaşamla İlişkilendirme

📌 Örnek 1:
Bir ağacın her yıl 2 metre uzadığı bir örüntü düşünelim.
✅ İlk yıl 3 metre ise, 5. yıl kaç metre olur?
✅ 3, 5, 7, 9, 11 → 5. yıl 11 metre olur.

📌 Örnek 2:
Bir merdiven her basamakta 2 katına çıkıyorsa,
✅ İlk basamak 2 adım ise, 4. basamakta kaç adım olur?
✅ 2, 4, 8, 16 → 4. basamakta 16 adım olur.

✍ Etkinlik:

1. Bir tavşan her ay iki katına çıkıyorsa, 4. ay kaç tavşan olur? (Başlangıçta 1 tavşan var)
2. Bir şirket her ay 500 TL kar artırıyorsa, 6. ayda toplam karı ne kadar olur? (Başlangıç 2.000 TL)

5.1.9. Çarpanlar ve Katlar

1. Çarpan Nedir?

📌 Bir sayının çarpanları, o sayıyı tam bölebilen sayılardır.
📌 Çarpan bulma, çarpma işleminin tersidir.

📌 Örnek:
12 sayısının çarpanlarını bulalım:
✅ 1 × 12 = 12
✅ 2 × 6 = 12
✅ 3 × 4 = 12
🔹 Çarpanlar: 1, 2, 3, 4, 6, 12

📌 Örnek:
20 sayısının çarpanlarını bulun:
✅ 1 × 20, 2 × 10, 4 × 5
🔹 Çarpanlar: 1, 2, 4, 5, 10, 20

✍ Etkinlik:

1. 15, 24 ve 36 sayılarının çarpanlarını listeleyin.
2. En küçük çarpanı her zaman hangi sayı olur?

2. Kat Nedir?

📌 Bir sayının katları, o sayının belirli bir sayı ile çarpılmasıyla elde edilir.
📌 Katlar sonsuzdur, çünkü sayı sürekli büyüyebilir.

📌 Örnek:
5’in ilk 5 katını yazalım:
✅ 5 × 1 = 5
✅ 5 × 2 = 10
✅ 5 × 3 = 15
✅ 5 × 4 = 20
✅ 5 × 5 = 25
🔹 5’in katları: 5, 10, 15, 20, 25, …

📌 Örnek:
7’nin ilk 5 katını bulun:
✅ 7, 14, 21, 28, 35

✍ Etkinlik:

1. 4, 6 ve 9’un ilk beş katını yazın.
2. Hangi sayıların katları çarpanlarından daha fazladır?

3. Asal Sayılar ve Bileşik Sayılar

📌 Asal sayılar, yalnızca 1 ve kendisine bölünebilen sayılardır.
📌 Bileşik sayılar, birden fazla çarpanı olan sayılardır.

📌 Örnek:
✅ Asal Sayılar: 2, 3, 5, 7, 11, 13, 17, 19, 23…
✅ Bileşik Sayılar: 4, 6, 8, 9, 10, 12, 14…

📌 Özel Durum:
🔹 1 asal değildir.
🔹 2 en küçük ve tek çift asal sayıdır.

✍ Etkinlik:

1. 1’den 30’a kadar olan asal sayıları belirleyin.
2. Hangi sayı asal mı bileşik mi? 19, 27, 31, 45

4. En Büyük Ortak Bölen (EBOB)

📌 İki veya daha fazla sayının ortak çarpanlarının en büyüğüdür.

📌 Örnek:
18 ve 24’ün EBOB’unu bulalım.

🔹 18’in çarpanları: 1, 2, 3, 6, 9, 18
🔹 24’ün çarpanları: 1, 2, 3, 4, 6, 8, 12, 24
✅ Ortak çarpanlar: 1, 2, 3, 6
✅ EBOB = 6

✍ Etkinlik:

1. 16 ve 28’in EBOB’unu bulun.
2. 40 ve 50’nin EBOB’unu hesaplayın.

5. En Küçük Ortak Kat (EKOK)

📌 İki veya daha fazla sayının ortak katlarının en küçüğüdür.

📌 Örnek:
6 ve 8’in EKOK’unu bulalım.

🔹 6’nın katları: 6, 12, 18, 24, 30, 36, …
🔹 8’in katları: 8, 16, 24, 32, 40, …
✅ Ortak katlar: 24, 48, 72, …
✅ EKOK = 24

✍ Etkinlik:

1. 12 ve 15’in EKOK’unu hesaplayın.
2. 9 ve 18’in EKOK’unu bulun.

6. Gerçek Hayatta Çarpanlar ve Katlar

📌 Örnek 1:
Bir pastanede her 6 saatte bir pasta ve 8 saatte bir kek yapılıyor. İkisi birden kaç saatte bir yapılır?
✅ Çözüm: EKOK(6, 8) = 24
✅ Cevap: Her 24 saatte bir birlikte yapılır.

📌 Örnek 2:
İki zil biri 20 dakikada, diğeri 25 dakikada bir çalıyor. İkisi birlikte kaç dakikada bir çalar?
✅ Çözüm: EKOK(20, 25) = 100 dakika
✅ Cevap: Her 100 dakikada bir çalarlar.

✍ Etkinlik:

1. Bir market her 15 günde bir indirim yapıyor. Başka bir market 20 günde bir indirim yapıyor. İki market aynı gün indirime kaç günde bir girer?
2. Bir öğrenci 4 günde bir matematik, 6 günde bir fen çalışıyor. İkisini aynı gün çalışması için kaç gün beklemesi gerekir?