İçindekiler
6.Sınıf Cebirsel İfadeler Konu Anlatımı
Cebirsel İfadeler 6.Sınıf Matematikte bilinmeyen değerleri temsil etmek için harfler kullanılır. Sayılar ve harflerin birleşimiyle oluşan ifadelere cebirsel ifadeler denir. 6. sınıf matematik dersinin “Cebirsel İfadeler” konusu, öğrencilerin matematiksel düşünme becerilerini geliştiren önemli bir konudur. Cebirsel ifadeler, sayı ve harfleri içeren matematiksel ifadeler olup, bu ifadelerle yapılan işlemler temel aritmetik becerileri ve algoritmalarını öğrenmek için önemlidir. Bu konu anlatımında, cebirsel ifadelerin tanımı, terimler, katsayılar ve değişkenler hakkında detaylı bilgiler verilir. Ayrıca, cebirsel ifadelerle yapılan toplama, çıkarma ve çarpma gibi işlemler üzerine örnek sorularla konuyu pekiştirebilirsiniz. Bu çalışma, öğrencilerin cebirsel ifadeleri anlamalarına ve kullanmalarına yardımcı olacaktır.
Bu ünitede şunları öğreneceğiz:
✅ Cebirsel ifade nedir?
✅ Terim, katsayı ve değişken kavramları
✅ Cebirsel ifadelerde toplama ve çıkarma işlemleri
✅ Cebirsel ifadelerin günlük hayattaki kullanımı
Cebirsel İfade Nedir ve Nasıl Gösterilir?
Matematikte bilinmeyen veya değişebilen değerleri ifade etmek için harfler ve sayılar kullanılır. Bu tür ifadelere cebirsel ifadeler denir.
Cebirsel İfade Nedir?
📌 Tanım:
Bir veya birden fazla bilinmeyen (değişken) ve sayıları içeren matematiksel ifadelere cebirsel ifadeler denir.
✔ Örnekler:
- x + 5
- 2y – 3
- 3a + 7b – 4
✅ Dikkat:
- x, y, a, b gibi harfler değişken (bilinmeyen) olarak adlandırılır.
- Harflerin önündeki sayılar katsayıdır.
- Sabit sayılar değişmez ve her zaman aynıdır.
Cebirsel İfadelerin Bileşenleri
Cebirsel ifadeler üç temel bileşenden oluşur:
✔ Değişken (Bilinmeyen) → x, y, a, b gibi harfler
✔ Katsayı → Değişkenin önündeki çarpan (3x → 3 katsayıdır)
✔ Sabit Terim → Değişken içermeyen sayı (2x + 5 → 5 sabit terimdir)

- 4x → “4” katsayı, “x” değişken
- 3y → “3” katsayı, “y” değişken
- -7 → Sabit terim
Cebirsel İfadelerin Günlük Hayattaki Kullanımı
Cebirsel ifadeler, günlük hayatta birçok alanda kullanılır.
✔ Yaş Problemleri:
Bir kişinin yaşı x ise, 5 yıl sonraki yaşı x + 5 olarak ifade edilir.
✔ Ücret ve Maaş Hesaplama:
Bir işçinin saatlik ücreti a TL ise, 8 saatlik kazancı 8a TL olur.
✔ Mesafe – Hız – Zaman Hesaplamaları:
Bir araç t saat boyunca v km/saat hızla giderse, toplam yol: v × t olur.
✔ Alan – Çevre Hesaplamaları:
Bir karenin kenarı x cm ise,
- Çevresi: 4x cm
- Alanı: x² cm² olur.
Örnek Sorular ve Çözümleri
✅ Soru 1: Aşağıdaki ifadelerden hangisi bir cebirsel ifadedir?
A) 5 + 7
B) x – 4
C) 12 ÷ 3
D) 100 – 25



Cebirsel İfadelerde Toplama ve Çıkarma İşlemi
Cebirsel ifadelerde toplama ve çıkarma işlemi, benzer terimlerin birleştirilmesiyle yapılır.
Bu bölümde:
✅ Benzer ve farklı terimleri ayırt etme
✅ Cebirsel ifadelerde toplama işlemi
✅ Cebirsel ifadelerde çıkarma işlemi
✅ Örnek problem çözümleri konularını öğreneceğiz.
Benzer ve Farklı Terimler
📌 Benzer terimler: Değişkenleri ve üslü ifadeleri aynı olan terimlerdir.
📌 Farklı terimler: Değişkenleri farklı olan terimlerdir.
✅ Örnekler:
✔ 3x ve 5x benzer terimlerdir.
✔ 4y ve -2y benzer terimlerdir.
✔ 2a ve 3b farklı terimlerdir.
Cebirsel İfadelerde Toplama İşlemi
📌 Benzer terimler toplanırken katsayılar toplanır, değişken aynı kalır.



Cebirsel İfadelerde Çıkarma İşlemi
📌 Benzer terimler çıkarılırken katsayılar birbirinden çıkarılır, değişken aynı kalır.

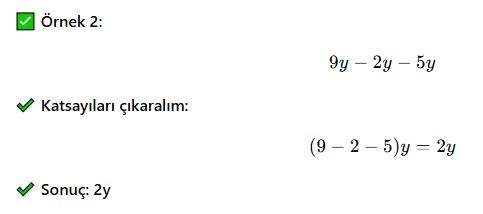

Örnek Sorular ve Çözümleri



Cebirsel İfadelerle Problem Çözme
Cebirsel ifadeler, günlük hayatta karşılaştığımız birçok problemi çözmek için kullanılır. Özellikle yaş problemleri, hız-zaman problemleri, gelir-gider hesaplamaları, alan-çevre hesaplamaları gibi konularda cebirsel ifadeler oldukça faydalıdır.
Bu bölümde:
✅ Cebirsel ifadeler kullanarak problem çözme teknikleri
✅ Örnek problemlerin adım adım çözümü
✅ Cebirsel ifadelerle denklem kurma ve çözme konularını öğreneceğiz.
Günlük Hayatta Cebirsel İfadelerle Problem Çözme
📌 Yaş Problemleri
✅ Örnek 1:
Ahmet’in yaşı x ise, 5 yıl sonraki yaşı nasıl ifade edilir?

📌 Hız ve Yol Problemleri
✅ Örnek 2:
Bir araç saatte v km hızla gidiyorsa, t saat sonunda kaç km yol alır?

📌 Gelir ve Gider Problemleri
✅ Örnek 3:
Bir işçinin günlük maaşı m TL ise, 30 günde kazandığı toplam maaş kaç TL olur?

📌 Alan ve Çevre Problemleri
✅ Örnek 4:
Bir karenin kenar uzunluğu a cm ise, çevresi nasıl bulunur?

Denklem Kurarak Problem Çözme
📌 Örnek 1:
Bir sayının 3 katının 5 fazlası 23 ediyor. Bu sayıyı bulalım.

📌 Örnek 2:
Bir çiftlikte inek sayısı koyun sayısının 2 katıdır. Eğer çiftlikte k koyun varsa, toplam hayvan sayısını cebirsel ifade olarak yazalım.

Örnek Sorular ve Çözümleri
✅ Soru 1: Bir öğrencinin yaşı x olsun. 3 yıl sonraki yaşını gösteren cebirsel ifade nedir?
A) x + 3
B) x – 3
C) 3x
D) x ÷ 3

✅ Soru 2: Bir karenin kenar uzunluğu a cm’dir. Çevresi kaç cm’dir?
A) 2a
B) 3a
C) 4a
D) a²

✅ Soru 3: Bir markette elmanın fiyatı x TL, armudun fiyatı y TL’dir. 2 kg elma ve 3 kg armut alırsak toplam ödeme ne olur?
A) 2x + 3y
B) x + y
C) 3x + 2y
D) 5x + 5y

6.Sınıf Cebirsel İfadeler Ünitesi Değerlendirme Testi
1. Aşağıdaki ifadelerden hangisi bir cebirsel ifadedir?
A) 10 + 5
B) x – 4
C) 8 × 3
D) 100 ÷ 25
2. 3x + 7 cebirsel ifadesinde, x’in katsayısı kaçtır?
A) 3
B) 7
C) x
D) 10
3. Bir dikdörtgenin kısa kenarı x cm, uzun kenarı 2x cm’dir. Dikdörtgenin çevresi nasıl ifade edilir?
A) 2x + x
B) 2(x + 2x)
C) 2x × x
D) x + 2x
4. Bir öğrencinin yaşı x olsun. 5 yıl sonraki yaşını gösteren cebirsel ifade nedir?
A) x + 5
B) x – 5
C) 5x
D) x ÷ 5
5. Bir arabanın saatte v km hızla gittiği biliniyor. Araba t saat boyunca hareket ederse, toplam gittiği mesafeyi gösteren cebirsel ifade nedir?
A) v + t
B) v × t
C) v – t
D) v ÷ t
6. Aşağıdaki işlemin sonucu nedir?
![]()
A) 7x
B) 5x
C) 9x
D) 6x
7. 5a + 4b – 2a + 3b işleminin sonucu nedir?
A) 3a + 7b
B) 7a + 1b
C) 3a + 1b
D) 7a + 7b
8. Bir işçinin günlük maaşı m TL’dir. 30 günde kazandığı toplam maaşı gösteren cebirsel ifade nedir?
A) 30m
B) m + 30
C) 30 + m
D) 30 ÷ m
9. 10y – 3y – 2y işleminin sonucu nedir?
A) 5y
B) 4y
C) 3y
D) 6y
10. Bir çiftlikte inek sayısı koyun sayısının 3 katıdır. Eğer çiftlikte k koyun varsa, toplam hayvan sayısını gösteren cebirsel ifade nedir?
A) 3k
B) 4k
C) 2k
D) k + 3k
Cevap Anahtarı:
- B) x – 4
- A) 3
- B) 2(x + 2x)
- A) x + 5
- B) v × t
- B) 5x
- A) 3a + 7b
- A) 30m
- A) 5y
- D) k + 3k
