6.Sınıf Matematik Kümeler Konu Anlatımı

Matematikte küme, belirli nesnelerin veya sayıların bir araya gelerek oluşturduğu gruplardır. Günlük hayatta sınıflandırma, gruplama, istatistik, veri analizi ve programlama gibi birçok alanda kümeler kullanılır.

Bu ünitede:
✅ Küme kavramını ve gösterimlerini öğreneceğiz.
✅ Kümeleri liste yöntemi ve Venn şeması ile göstereceğiz.
✅ Boş küme, eşit küme, alt küme ve evrensel küme kavramlarını tanıyacağız.
✅ Kümelerde birleşim, kesişim ve fark işlemlerini öğreneceğiz.

Küme Kavramı ve Gösterimleri

Matematikte belirli nesnelerin veya elemanların bir araya gelerek oluşturduğu topluluğa küme denir. Kümeler, nesneleri veya sayıları sınıflandırarak düzenli bir şekilde gruplamak için kullanılır.

Küme Nedir?

Birbirinden farklı nesneler, sayılar veya elemanlar küme adı verilen gruplar içinde toplanabilir.

✅ Örnek Kümeler:

A = {elma, armut, muz} (Meyve kümesi)
B = {1, 2, 3, 4, 5} (Doğal sayı kümesi)
C = {a, e, i, o, u} (Sesli harfler kümesi)

🔹 Dikkat: Kümelerde aynı eleman iki kez yazılmaz!

❌ Yanlış: A = {elma, armut, muz, elma}
✔ Doğru: A = {elma, armut, muz}

Küme Gösterim Yöntemleri

Bir küme üç farklı şekilde gösterilebilir:

A. Liste Yöntemiyle Gösterim

Kümenin elemanları küme parantezi { } içinde, virgülle ayrılarak yazılır.

✅ Örnek:
Sesli harfler kümesi:

B. Ortak Özellik Yöntemiyle Gösterim

Elemanları belirli bir özelliğe göre tanımlayarak gösteririz.

✅ Örnek:
“1 ile 10 arasındaki çift sayılar kümesi”

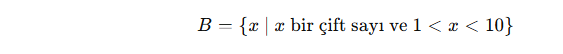
C. Venn Şeması ile Gösterim

Kümenin elemanları bir kapalı eğri içinde gösterilir.

✅ Örnek:
Renkler kümesi:

Küme Eleman Sayısı

Bir kümede bulunan elemanların toplam sayısı eleman sayısı olarak adlandırılır ve |A| ile gösterilir.

✅ Örnek:
A = {1, 2, 3, 4, 5}
|A| = 5 (5 elemanlı bir küme)

Boş Küme (Ø)

İçinde hiçbir eleman bulunmayan kümeye boş küme denir ve Ø veya {} ile gösterilir.

✅ Örnek:

“10’dan küçük asal olmayan tam sayılar” kümesi boş kümedir.
“Hiç katılımcı olmayan bir yarışma” kümesi boş kümedir.

Kümeler Örnek Sorular ve Çözümleri

✅ Soru 1:
A = {k, l, m, n} kümesinin eleman sayısını bulun.

Çözüm:
Kümede 4 eleman vardır, yani |A| = 4

✅ Soru 2:
Aşağıdaki kümelerden hangisi boş kümedir?

A) {0}
B) {Ø}
C) {}
D) {1, 2, 3}

Çözüm:
✔ {} boş kümedir. (Cevap: C)
❌ {0} kümesinde 0 bir elemandır, boş değildir.
❌ {Ø} kümesi boş kümenin bir eleman olduğu kümedir.

Eşit Küme, Alt Küme ve Evrensel Küme

Kümeler arasında bazı özel ilişkiler vardır. Eşit kümeler, alt kümeler ve evrensel küme, matematikte kümelerle işlemler yaparken önemli kavramlardır.

Eşit Küme Nedir?

İki küme aynı elemanlara sahipse, bu kümeler eşit kümedir ve = sembolü ile gösterilir.

✅ Örnek:
A = {2, 4, 6, 8}
B = {8, 6, 4, 2}

✔ A = B çünkü her iki kümede de aynı elemanlar vardır. Elemanların sırası önemli değildir!

❌ Yanlış:
A = {a, b, c}
B = {a, c}
A ≠ B, çünkü B kümesinde “b” elemanı yoktur.

Alt Küme (⊆) Nedir?

Bir kümenin tüm elemanları, başka bir kümenin içinde bulunuyorsa, bu küme diğer kümenin alt kümesi olur.

✔ Alt küme sembolü: ⊆

✅ Örnek:
A = {1, 2, 3, 4}
B = {2, 4}

✔ B ⊆ A çünkü B kümesinin tüm elemanları A kümesinde bulunuyor.

✔ Her küme kendisinin alt kümesidir!
✔ Boş küme, her kümenin alt kümesidir!

Alt Küme Sayısı Nasıl Bulunur?

Bir kümenin eleman sayısı “n” ise, o kümenin alt küme sayısı şu formülle bulunur:

✅ Örnek:
A = {x, y, z} kümesi için:
n = 3, alt küme sayısı:

✔ Alt kümeler: {}, {x}, {y}, {z}, {x, y}, {x, z}, {y, z}, {x, y, z}

Evrensel Küme (E) Nedir?

Çalışılan tüm kümeleri kapsayan en geniş kümeye evrensel küme denir ve E harfi ile gösterilir.

✅ Örnek:

A = {1, 2, 3}
B = {2, 3, 4, 5}
Evrensel Küme: E = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}

✔ A ve B kümeleri, E kümesinin içinde bulunur.

Örnek Sorular ve Çözümleri

✅ Soru 1:
A = {a, b, c, d}
B = {a, c}

B kümesi A’nın alt kümesi midir?

Çözüm:
B’nin tüm elemanları A’da var.
✔ B ⊆ A

✅ Soru 2:
A = {2, 4, 6, 8}
B = {4, 8, 6, 2}

A ve B eşit küme midir?

Çözüm:
A ve B’nin elemanları tamamen aynı, sadece sıraları farklı.
✔ A = B

✅ Soru 3:
A = {1, 2, 3} kümesinin alt küme sayısını bulun.

Çözüm:
A’nın 3 elemanı var.
Alt küme sayısı:

✔ Cevap: 8 alt küme vardır.

Kümelerde Birleşim, Kesişim ve Fark İşlemleri

Kümeler arasında bazı işlemler yaparak elemanların ortak ve farklı yönlerini belirleyebiliriz. Bu işlemler arasında birleşim, kesişim ve fark işlemleri bulunur.

Birleşim Kümesi ( ∪ )

Birleşim, iki kümenin tüm elemanlarını içeren yeni bir küme oluşturur. A ∪ B, A ve B kümelerinin tüm elemanlarını içerir.

✔ Birleşim Kümesi Kuralı:

$\text{(A kümesinin elemanları)} + \text{(B kümesinin elemanları)} – \text{(Ortak elemanlar)}$

✅ Örnek:
A = {1, 2, 3}
B = {3, 4, 5}

🔹 Dikkat: Ortak elemanlar sadece bir kez yazılır!

Kesişim Kümesi ( ∩ )

Kesişim, iki kümenin ortak elemanlarını içeren yeni bir küme oluşturur. A ∩ B, yalnızca A ve B’de ortak olan elemanlardan oluşur.

✅ Örnek:
A = {a, b, c, d}
B = {b, d, e, f}

🔹 Dikkat: Kesişim kümesi boş olabilir! Eğer iki kümenin ortak elemanı yoksa, A ∩ B = Ø olur.

Fark Kümesi ( A – B veya B – A )

Fark işlemi, bir kümenin elemanlarından diğer kümenin elemanlarını çıkartarak oluşturulur.

✔ Kural:

✅ Örnek:
A = {1, 2, 3, 4}
B = {3, 4, 5, 6}

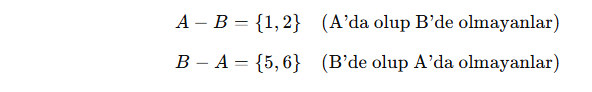
Örnek Sorular ve Çözümleri

✅ Soru 1:
A = {2, 4, 6, 8}
B = {6, 8, 10, 12}

A ∪ B birleşim kümesini bulun.

Çözüm:
Tüm elemanları birleştiriyoruz, ortak olanları bir kez yazıyoruz:

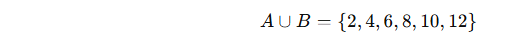
✅ Soru 2:
A = {a, b, c, d, e}
B = {c, d, e, f, g}

A ∩ B kesişim kümesini bulun.

Çözüm:
İki kümenin ortak elemanlarını alıyoruz:

✅ Soru 3:
X = {1, 2, 3, 4, 5, 6}
Y = {4, 5, 6, 7, 8, 9}

X – Y fark kümesini bulun.

Çözüm:
X’te olup Y’de olmayanları yazıyoruz:

Kümeler Ünitesi Değerlendirme Testi

1. A = {2, 4, 6, 8} ve B = {4, 8, 10, 12} kümeleri veriliyor.

A ∪ B birleşim kümesi nedir?

A) {2, 4, 6, 8, 10, 12}
B) {4, 8}
C) {2, 6, 10, 12}
D) {2, 4, 6, 8}

2. Küme kavramı için aşağıdakilerden hangisi doğrudur?

A) Küme elemanları tekrarlanabilir.
B) Küme elemanlarının sırası önemlidir.
C) Küme elemanları süslü parantez {} içinde gösterilir.
D) Küme boş olamaz.

3. A = {1, 3, 5, 7} ve B = {3, 5, 9, 11} kümeleri veriliyor.

A ∩ B kesişim kümesi nedir?

A) {1, 3, 5, 7, 9, 11}
B) {3, 5}
C) {1, 7, 9, 11}
D) {}

4. X kümesi boş küme ise aşağıdaki ifadelerden hangisi doğrudur?

A) X kümesi en az bir eleman içerir.
B) X kümesi evrensel kümedir.
C) X kümesinin eleman sayısı 0’dır.
D) X kümesi alt küme olamaz.

5. A = {a, b, c, d} ve B = {b, d} veriliyor.

B kümesi A kümesinin alt kümesi midir?

A) Hayır, çünkü B’de daha az eleman var.
B) Evet, çünkü B’nin tüm elemanları A’da var.
C) Hayır, çünkü A’daki tüm elemanlar B’de olmalı.
D) B kümesi boş kümedir.

6. Bir kümenin alt küme sayısını bulmak için hangi formül kullanılır?

7. Evrensel küme nedir?

A) Tüm alt kümeleri içinde bulunduran kümedir.
B) İçinde sadece asal sayılar olan kümedir.
C) Sadece iki eleman içeren kümedir.
D) Birleşim kümesine eşit olan kümedir.

8. A = {2, 4, 6, 8} ve B = {4, 8, 10, 12} veriliyor.

A – B fark kümesi nedir?

A) {2, 6}
B) {4, 8}
C) {10, 12}
D) {2, 6, 10, 12}

9. Eğer A kümesi B kümesinin alt kümesi ise aşağıdaki ifadelerden hangisi doğrudur?

A) A’daki her eleman B’de bulunur.
B) A’daki elemanlar B’den daha fazladır.
C) A ve B’nin birleşimi boş kümedir.
D) A kümesi evrensel kümedir.

10. Eğer iki kümenin kesişimi boş küme ise bu kümeler için ne söylenebilir?

A) Ortak elemanları yoktur.
B) Aynı elemanlara sahiptirler.
C) Birleşimleri de boş kümedir.
D) İkisinin de alt kümesi aynıdır.

Cevap Anahtarı:

6.Sınıf Matematik Kümeler Konu Anlatımı ve Örnek Sorular

6.Sınıf Matematik Kümeler Konu Anlatımı