Oran ve Orantı Konu Anlatımı

Matematikte oran ve orantı, farklı büyüklükleri karşılaştırmak ve ilişkilerini anlamak için kullanılır. Oran, iki çokluğun birbirine bölünmesiyle elde edilir. Orantı ise iki oran arasındaki eşitliktir.

Bu ünitede, oranın temel özelliklerinden başlayarak, doğru ve ters orantı kavramlarını öğrenecek, orantı sabitlerini hesaplayacak ve günlük hayatta karşımıza çıkan oran-orantı problemlerini çözeceğiz.

Şimdi ilk konumuz olan “Oranda Çokluklardan Birinin 1 Olması Durumunda Diğerinin Alacağı Değer” ile başlayalım.

Oranda Çokluklardan Birinin 1 Olması Durumunda Diğerinin Alacağı Değer

Oran, iki çokluğun birbirine bölünmesiyle elde edilen bir ilişkidir. Bir büyüklük 1 olduğunda, diğer büyüklüğün nasıl değiştiğini belirleyerek oranları daha kolay yorumlayabiliriz.

Oran Nedir?

İki çokluğun birbirine oranı şu şekilde ifade edilir:

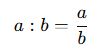
Burada:

• a ve b farklı büyüklüklerdir.
• b sıfırdan farklıdır.

📌 Örnek:
Bir sınıfta kız öğrenci sayısının, erkek öğrenci sayısına oranı 3 : 5 olsun.

• Eğer kız öğrenci sayısı 3 ise, erkek öğrenci sayısı 5 olur.
• Eğer kız öğrenci sayısı 1 olsaydı, erkek öğrenci sayısı 5 ÷ 3 olurdu.
• Bir öğrencinin karşılığı:

✔ Sonuç: Eğer çokluklardan biri 1 olarak verilirse, diğer çokluğun değeri oran kullanılarak hesaplanabilir.

📌 Örnek :
Bir fabrikanın üretim hızı şu şekildedir: Makinelerin çalışma süresinin üretilen parça sayısına oranı 5 : 20’dir.

• Eğer makineler 1 saat çalışırsa, kaç parça üretilir?

✅ Çözüm:

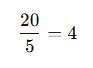
✔ Sonuç: Makineler 1 saat çalışırsa, 4 parça üretilir.

📌 Örnek Problemler:

1. Bir otomobilin gittiği yolun harcadığı benzine oranı 240 km : 20 L’dir. Eğer otomobil 1 litre benzin harcarsa kaç km yol gider?
2. Bir bahçede dikilen fidanların sayısının sulanan alan miktarına oranı 15 : 45’tir. Eğer bahçede 1 fidan olursa kaç metrekare sulanır?
3. Bir çiftlikte inek sayısının koyun sayısına oranı 4 : 9’dur. Eğer çiftlikte 1 inek olursa kaç koyun bulunur?

Birbirine Oranı Verilen İki Çokluktan Biri Verildiğinde Diğerini Bulma

Matematikte oran, iki çokluğun birbirine bölünmesiyle elde edilen bir ilişkiyi ifade eder. Eğer iki büyüklüğün oranı verilirse ve bu büyüklüklerden biri biliniyorsa, diğer büyüklük bulunabilir.

1. Oranı Kullanarak Diğer Çokluğu Bulma

İki büyüklüğün oranı şu şekilde ifade edilir:

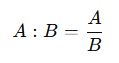
Eğer A’nın değeri verilirse, B bulunabilir veya B’nin değeri verilirse, A bulunabilir.

📌 Örnek 1:
Bir sınıfta kız öğrencilerin sayısının erkek öğrencilere oranı 2 : 3 olarak verilmiştir.
Eğer sınıfta 8 kız öğrenci varsa, erkek öğrenci sayısı kaçtır?

✅ Çözüm:
Verilen oran: 2 : 3
Bu oran şu anlama gelir:

• Kız sayısı = 2x
• Erkek sayısı = 3x

Şimdi kız sayısını 8’e eşitleyelim:

📌 Örnek 2:
Bir ağaçtaki elma sayısının portakal sayısına oranı 5 : 2’dir.
Eğer ağaçta 20 elma varsa, kaç portakal vardır?

✅ Çözüm:
Verilen oran: 5 : 2
Bu oran şu anlama gelir:

• Elma sayısı = 5x
• Portakal sayısı = 2x

Şimdi elma sayısını 20’ye eşitleyelim:

📌 Örnek 3:
Bir fabrikanın ürettiği ürünlerin erkek ve kadın çalışanlara dağılım oranı 7 : 5’tir.
Eğer kadın çalışanlara 50 ürün düşüyorsa, erkek çalışanlara kaç ürün düşer?

✅ Çözüm:
Verilen oran: 7 : 5
Bu oran şu anlama gelir:

• Erkek çalışanlara düşen ürün = 7x
• Kadın çalışanlara düşen ürün = 5x

Şimdi kadın çalışanlara düşen ürün sayısını 50’ye eşitleyelim:

2. Genel Formül

İki büyüklüğün oranı:

📌 Örnek Problemler:

1. Bir markette satılan süt şişelerinin su şişelerine oranı 3 : 5’tir. Eğer markette 27 şişe süt varsa, kaç şişe su vardır?
2. Bir şirkette mühendislerin sayısının teknisyenlere oranı 4 : 3’tür. Eğer şirkette 24 mühendis varsa, kaç teknisyen vardır?
3. Bir okulda kız ve erkek öğrencilerin oranı 7 : 8’dir. Eğer okulda 56 kız öğrenci varsa, erkek öğrenci sayısını bulun.
4. Bir çiftlikte koyunların sayısının ineklerin sayısına oranı 5 : 2’dir. Eğer çiftlikte 40 koyun varsa, kaç inek vardır?

Orantı

Matematikte orantı, iki veya daha fazla oranın eşit olması durumudur. Orantılar, doğru orantı ve ters orantı olmak üzere ikiye ayrılır.

1. Orantı Nedir?

Eğer iki oran eşit olarak yazılabiliyorsa, bu bir orantıdır.

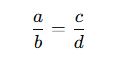
Burada:

• a ve b bir oranı,
• c ve d diğer oranı temsil eder.
• b ≠ 0 ve d ≠ 0 olmalıdır.

📌 Örnek:

2. Doğru Orantı ve Ters Orantı

✔ Doğru Orantı: Bir büyüklük artarken diğeri de aynı oranda artıyorsa, doğru orantı vardır.

✔ Ters Orantı: Bir büyüklük artarken diğeri aynı oranda azalıyorsa, ters orantı vardır.

3. İçler Dışlar Çarpımı Kullanımı

Orantılarda bilinmeyen bir değeri bulmak için içler dışlar çarpımı yapılır.

4. Orantılı Büyüklükleri Karşılaştırma

Eğer bir problemde iki çokluğun oranı verilmişse ve bir değer eksikse, orantı kullanılarak bilinmeyen değer bulunabilir.

📌 Örnek 3:
Bir okulda öğretmenlerin sayısının öğrencilere oranı 1 : 20’dir. Eğer okulda 8 öğretmen varsa, kaç öğrenci vardır?

✅ Çözüm:
Öğretmenlerin öğrencilerle oranı:

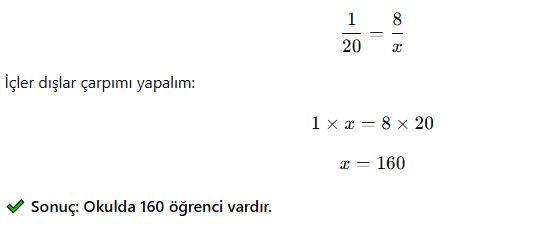
📌 Örnek 4:
Bir çikolata fabrikasında üretilen çikolataların sayısının işçi sayısına oranı 4 : 1’dir. Eğer fabrikada 25 işçi çalışıyorsa, kaç çikolata üretilmiştir?

5. Orantı Özellikleri

1️⃣ Bir orantıda içler ve dışlar çarpımı eşittir:

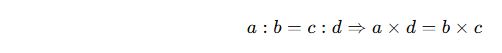
2️⃣ Doğru orantıda biri artarsa diğeri de artar.
3️⃣ Ters orantıda biri artarsa diğeri azalır.

📌 Örnek Problemler:

1. Bir okulda öğrencilerin öğretmenlere oranı 25 : 1’dir. Eğer okulda 30 öğretmen varsa, öğrenci sayısını bulun.
2. Bir çiftlikte koyunların sayısının ineklerin sayısına oranı 7 : 4’tür. Eğer çiftlikte 35 koyun varsa, kaç inek vardır?
3. Bir marangoz her 2 saatte 3 sandalye yapmaktadır. 10 saat çalıştığında kaç sandalye yapar?
4. Bir fabrikanın üretim oranı 8 : 3’tür. Eğer fabrika 24 saat çalışarak 96 parça üretirse, 9 saat çalışarak kaç parça üretir?

Doğru Orantılı İki Çokluk Arasındaki İlişki

Matematikte iki çokluk biri artarken diğeri de aynı oranda artıyorsa veya biri azalırken diğeri de aynı oranda azalıyorsa, bu çokluklar doğru orantılıdır.

1. Doğru Orantı Nedir?

İki çokluk doğru orantılıysa, aralarındaki oran sabit kalır.

Eğer x ve y doğru orantılı ise şu eşitlik sağlanır:

Burada k bir orantı sabitidir ve her zaman sabit bir değerdir.

Bu ifade çarpım şeklinde de yazılabilir:

✔ Özellik:

• x arttığında y de artar.
• x azaldığında y de azalır.
• İki çokluk arasındaki oran değişmezdir.

2. Doğru Orantıya Örnekler

📌 Örnek 1:
Bir iş yerinde çalışan saat arttıkça üretilen ürün miktarı da artmaktadır. Eğer 5 saat çalışıldığında 20 ürün üretiliyorsa, 8 saat çalışıldığında kaç ürün üretilir?

✅ Çözüm:
İşçi saatleri ve üretilen ürünler doğru orantılıdır.

📌 Örnek 2:
Bir araba 2 saatte 150 km yol alıyorsa, 5 saatte kaç km yol alır?

3. Doğru Orantının Formülü

Eğer x ve y doğru orantılıysa şu formül kullanılır:

Bu formülü kullanarak bilinmeyen değerleri bulabiliriz.

📌 Örnek Problemler:

1. Bir usta, 4 saatte 16 masa yapmaktadır. 10 saatte kaç masa yapar?
2. Bir kamyon 3 saatte 120 km gidiyorsa, 9 saatte kaç km gider?
3. Bir çiftçi, 5 günde 30 kg sebze topluyorsa, 12 günde kaç kg sebze toplar?
4. Bir öğrenci 2 saatte 60 soru çözüyor. 5 saatte kaç soru çözer?

Doğru Orantılı İki Çokluğa Ait Orantı Sabiti

Doğru orantılı iki çokluk arasında bir sabit oran bulunur ve bu orantı sabiti (k) olarak adlandırılır. Bu sabit, iki büyüklüğün birbirine oranı ile bulunur ve değişmez.

1. Orantı Sabiti Nedir?

Eğer x ve y doğru orantılıysa, bunların oranı her zaman sabit olur:

Burada:

• x ve y doğru orantılı çoklukları,
• k ise orantı sabitini ifade eder.

Bu eşitliği çarpım şeklinde de yazabiliriz:

✔ Özellik:

• Orantı sabiti (k) her zaman aynıdır.
• x arttığında y de artar, x azaldığında y de azalır.
• Orantı sabiti, verilen herhangi iki x ve y değeri kullanılarak bulunabilir.

2. Orantı Sabiti Nasıl Bulunur?

📌 Örnek 1:
Bir araba 2 saatte 180 km gidiyor. Orantı sabiti (k) nedir?

✅ Çözüm:
Orantı sabitini bulmak için şu formülü kullanırız:

📌 Örnek 2:
Bir işçi 4 saatte 20 parça üretmektedir. Orantı sabitini (k) bulun.

📌 Örnek 3:
Bir kamyon 6 saatte 360 km gidiyor. Orantı sabiti nedir?

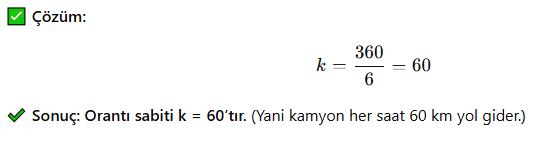
3. Orantı Sabiti Kullanılarak Bilinmeyeni Bulma

Eğer orantı sabiti k biliniyorsa, yeni x veya y değerlerini bulabiliriz.

📌 Örnek 4:
Bir makine her 5 dakikada 15 ürün üretiyor.
Makinenin orantı sabiti nedir?
Bu makine 12 dakikada kaç ürün üretir?

📌 Örnek 5:
Bir otobüs orantı sabiti 75 km/saat olacak şekilde yol alıyor.
Bu otobüs 8 saatte kaç km yol gider?

4. Orantı Sabiti Formülü

Doğru orantılı iki çokluk için:

📌 Örnek Problemler:

1. Bir usta, 3 saatte 12 sandalye yapmaktadır. Orantı sabitini bulun.
2. Bir araba 4 saatte 320 km yol gidiyor. Orantı sabitini bulun ve araba 7 saatte kaç km gider hesaplayın.
3. Bir işçi 2 saatte 50 kutu taşıyabiliyor. Orantı sabiti nedir? İşçi 5 saatte kaç kutu taşır?
4. Bir bahçıvan, 6 günde 24 ağaç dikiyor. 9 günde kaç ağaç diker?

Ters Orantılı İki Çokluk Arasındaki İlişki ve Orantı Sabiti

Matematikte iki çokluktan biri artarken diğeri azalıyorsa, bu çokluklar ters orantılıdır. Ters orantıda çarpım sabittir ve bir çokluk büyüdüğünde diğer küçülür.

1. Ters Orantı Nedir?

Eğer x ve y ters orantılıysa, şu eşitlik sağlanır:

Burada k orantı sabiti olup her zaman sabit bir değerdir.

✔ Özellikler:

• x arttıkça y azalır, x azaldıkça y artar.
• İki çokluğun çarpımı her zaman aynı kalır.

2. Ters Orantıya Örnekler

📌 Örnek 1:
Bir işi 4 işçi 12 saatte bitiriyorsa, 6 işçi aynı işi kaç saatte bitirir?

📌 Örnek 2:
Bir otomobil, 100 km yolu 5 saatte giderse, aynı yolu 10 saatte gitmek için hızı ne olmalıdır?

3. Ters Orantı Sabiti

Eğer x ve y ters orantılıysa, çarpımları sabittir:

📌 Örnek 3:
Bir su deposu, 2 musluk açıldığında 15 saatte doluyorsa, 3 musluk açıldığında kaç saatte dolar?

📌 Örnek 4:
Bir havuzu 4 pompa 18 saatte doldurabiliyor. Eğer 6 pompa çalıştırılırsa, havuz kaç saatte dolar?

4. Ters Orantı Özellikleri

1️⃣ x arttıkça y azalır, x azaldıkça y artar.
2️⃣ İki çokluğun çarpımı sabittir.
3️⃣ Ters orantıda oran yerine çarpım kullanılır:

📌 Örnek Problemler:

1. Bir işi 3 işçi 24 saatte yapıyorsa, aynı işi 6 işçi kaç saatte yapar?
2. Bir araba 60 km/s hızla bir yolu 4 saatte gidiyorsa, 80 km/s hızla kaç saatte gider?
3. 5 musluk bir havuzu 30 saatte dolduruyorsa, 10 musluk aynı havuzu kaç saatte doldurur?
4. Bir otobüs, 6 saatte 120 km gidiyorsa, aynı yolu 4 saatte gitmesi için hızı kaç olmalıdır?

Doğru ve Ters Orantıyla İlgili Problemler

Bu bölümde, doğru ve ters orantı konularında öğrendiklerimizi kullanarak gerçek hayat problemleri çözeceğiz.

Doğru Orantı: Biri artarken diğeri de artan, biri azalırken diğeri de azalan büyüklükler.

Ters Orantı: Biri artarken diğeri azalan büyüklükler.

1. Doğru Orantı Problemleri

📌 Örnek 1:
Bir bisikletli 2 saatte 30 km yol gidiyorsa, 5 saatte kaç km yol gider?

📌 Örnek 2:
Bir çiftlikte 6 işçi 12 günde bir tarlayı biçebiliyorsa, 9 işçi aynı tarlayı kaç günde biçer?

2. Ters Orantı Problemleri

📌 Örnek 3:
Bir su deposu 5 muslukla 18 saatte doluyorsa, 9 musluk açılırsa depo kaç saatte dolar?

📌 Örnek 4:
Bir araba 3 saatte 240 km yol alıyorsa, 5 saatte kaç km yol alır?

📌 Örnek 5:
Bir işçi 6 saatte 15 kutu taşıyabiliyorsa, 10 saatte kaç kutu taşır?

📌 Örnek 6:
Bir otobüs 60 km/saat hızla 4 saatte gidiyorsa, 90 km/saat hızla kaç saatte gider?

3. Karışık Orantı Problemleri

📌 Örnek 7:
Bir iş yeri, 6 işçi ile 20 günde tamamlanıyorsa, 10 işçi ile kaç günde tamamlanır?

📌 Örnek 8:
Bir öğrenci 2 saatte 60 soru çözüyor.
Aynı hızla 5 saatte kaç soru çözer?

4. Özet

✔ Doğru Orantı:

• Bir büyüklük arttığında, diğeri de artıyorsa doğru orantı vardır.
• Orantı sabiti değişmez.
• Formül:

✔ Ters Orantı:

• Bir büyüklük arttığında, diğeri azalırsa ters orantı vardır.
• Çarpımları sabittir.
• Formül:

📌 Örnek Problemler:

1. Bir traktör 4 saatte 100 dekar arazi sürüyor. Aynı hızla 7 saatte kaç dekar arazi sürer?
2. 8 işçi bir işi 24 günde yapıyorsa, 12 işçi aynı işi kaç günde yapar?
3. Bir otomobil 3 saatte 240 km gidiyorsa, 8 saatte kaç km gider?
4. Bir usta 5 günde 20 sandalye yapıyorsa, 15 günde kaç sandalye yapar?
5. Bir musluk 10 saatte bir havuzu dolduruyorsa, 4 musluk aynı havuzu kaç saatte doldurur?

Oran ve Orantı – 10 Soruluk Test

1.

Bir işçi 4 saatte 12 sandalye yapıyorsa, aynı işçi 10 saatte kaç sandalye yapar?

A) 30
B) 28
C) 32
D) 36

2.

Bir otomobil 2 saatte 180 km gidiyorsa, aynı hızla 5 saatte kaç km gider?

A) 400
B) 450
C) 300
D) 350

3.

Bir çiftlikte 6 işçi 12 günde tarlayı biçiyorsa, 9 işçi aynı tarlayı kaç günde biçer?

A) 9
B) 8
C) 7
D) 6

4.

Bir su deposu 5 muslukla 18 saatte doluyorsa, 9 musluk açılırsa kaç saatte dolar?

A) 8
B) 9
C) 10
D) 12

5.

Bir bisikletli 3 saatte 75 km gidiyorsa, 7 saatte kaç km yol gider?

A) 150
B) 200
C) 175
D) 210

6.

Bir araba 60 km/s hızla bir yolu 4 saatte gidiyorsa, 80 km/s hızla kaç saatte gider?

A) 2.5
B) 3
C) 3.5
D) 2

7.

Bir musluk bir havuzu 10 saatte dolduruyorsa, 4 musluk aynı havuzu kaç saatte doldurur?

A) 3
B) 2.5
C) 4
D) 5

8.

Bir öğrenci 2 saatte 60 soru çözüyor. Aynı hızla 5 saatte kaç soru çözer?

A) 120
B) 150
C) 140
D) 130

9.

Bir otobüs 6 saatte 120 km gidiyorsa, aynı yolu 4 saatte gitmesi için hızı kaç olmalıdır?

A) 160
B) 140
C) 180
D) 150

10.

8 işçi bir işi 24 günde yapıyorsa, 12 işçi aynı işi kaç günde yapar?

A) 16
B) 12
C) 14
D) 10

Cevap Anahtarı

1 – A
2 – B
3 – B
4 – C
5 – C
6 – D
7 – D
8 – B
9 – A
10 – A