Tam Sayılarla İşlemler Konu Anlatımı

Matematikte sayı kavramı, zamanla gelişmiş ve farklı sayı kümeleri ortaya çıkmıştır. İlköğretim yıllarında öğrendiğimiz doğal sayılar (0, 1, 2, 3, …), sadece pozitif değerleri içerir ve günlük hayatta sıkça kullanılır. Ancak matematiksel işlemleri genişletmek ve gerçek dünyadaki birçok durumu daha iyi ifade edebilmek için negatif sayılar da tanımlanmıştır. Pozitif ve negatif tam sayılar bir araya gelerek tam sayılar kümesini oluşturur.

Tam sayılar; günlük hayatta sıcaklık değerlerinden borç-alacak işlemlerine, deniz seviyesinin altındaki derinliklerden yüksek rakımlara kadar birçok alanda kullanılır. Bu ünitede, tam sayılarla yapılan temel işlemleri öğrenecek, toplama, çıkarma, çarpma ve bölme işlemlerinin mantığını kavrayacağız. Ayrıca, bu işlemlerin kurallarını ve matematiksel özelliklerini inceleyerek, problemler çözerek pekiştireceğiz.

Tam Sayılarla Toplama ve Çıkarma İşlemleri

Tam sayılarla toplama ve çıkarma işlemleri, günlük hayatta sıkça karşılaştığımız durumları modellememizi sağlar. Örneğin, hava sıcaklığı gece -5°C’ye düştüğünde ve sabah 3°C yükseldiğinde, yeni sıcaklığın nasıl hesaplanacağını bilmek önemlidir. Benzer şekilde, bir bankada 200 TL borcu olan bir kişi, hesabına 300 TL yatırdığında, yeni bakiyesini nasıl hesaplayacağını anlamalıdır.

Tam sayılarla yapılan işlemleri daha iyi kavrayabilmek için pozitif ve negatif sayıların toplama ve çıkarma işlemlerindeki kurallarını inceleyelim.

1. Pozitif ve Negatif Tam Sayılarla Toplama İşlemi

a) Aynı İşaretli Sayıların Toplanması

• İki pozitif tam sayı toplanırken, sayıların mutlak değerleri toplanır ve sonuç pozitif olur.
  Örnek: (+7) + (+3) = +10

• İki negatif tam sayı toplanırken, sayıların mutlak değerleri toplanır ve sonuç negatif olur.
  Örnek: (-5) + (-4) = -9

b) Farklı İşaretli Sayıların Toplanması

• İşaretleri farklı olan iki tam sayı toplanırken, büyük sayının mutlak değerinden küçük sayının mutlak değeri çıkarılır ve büyük sayının işareti sonuca yazılır.
  Örnek: (+8) + (-3) = +5
  Örnek: (-6) + (+2) = -4

2. Pozitif ve Negatif Tam Sayılarla Çıkarma İşlemi

Çıkarma işlemi, toplama işlemiyle ilişkilidir. Bir tam sayının çıkartılması, o sayının işaretinin değiştirilip toplama işlemi yapılmasıdır. Yani;

Örneğin:

• (+6) – (+4) = (+6) + (-4) = +2
• (-7) – (+2) = (-7) + (-2) = -9
• (+5) – (-3) = (+5) + (+3) = +8

Çıkarma işlemiyle ilgili şu temel kuralları unutmayalım:

• Pozitif bir sayıdan pozitif bir sayı çıkarılırken, mutlak değer farkı alınır.
• Negatif bir sayıdan negatif bir sayı çıkarılırken, işaret değiştirip toplama yapılır.
• Bir pozitif sayıdan negatif bir sayı çıkarıldığında, mutlak değerler toplanır ve sonuç pozitif olur.

Örnek Problemler

📌 Örnek 1: Bir banka hesabında -250 TL borcu olan bir kişi, 400 TL yatırıyor. Yeni bakiyesi kaç TL olur?
Çözüm:
(-250) + (+400) = +150 TL (Bakiye 150 TL oldu.)

📌 Örnek 2: Bir şehrin sabah sıcaklığı -3°C iken, öğleden sonra 5°C arttı. Yeni sıcaklık kaç °C olur?
Çözüm:
(-3) + (+5) = +2°C

Tam Sayılarda Toplama İşleminin Özellikleri

Matematikte işlemler belirli kurallara ve özelliklere göre yapılır. Toplama işlemi de bazı temel özelliklere sahiptir. Bu özellikleri anlamak, tam sayılarla yapılan işlemleri daha kolay ve hızlı yapmamıza yardımcı olur.

Tam sayılarda toplama işleminin 4 temel özelliği vardır:

1. Kapalılık Özelliği
2. Değişme (Yer Değiştirme) Özelliği
3. Birleşme (Gruplama) Özelliği
4. Etkisiz Eleman (Toplamaya Göre Birim Eleman) Özelliği

1. Kapalılık Özelliği

Matematikte bir işlem bir küme üzerinde yapıldığında, sonuç yine o kümenin bir elemanı oluyorsa, bu işleme kapalılık özelliği denir.

Tam sayılar kümesi (ℤ) toplama işlemine göre kapalıdır. Yani, iki tam sayının toplamı her zaman bir tam sayı olur.

📌 Örnekler:

• (+5) + (-3) = +2 (Sonuç bir tam sayıdır.)
• (-7) + (-4) = -11 (Sonuç bir tam sayıdır.)
• (+6) + (+9) = +15 (Sonuç bir tam sayıdır.)

Bu yüzden tam sayılar toplama işlemine göre kapalıdır.

2. Değişme (Yer Değiştirme) Özelliği

İki sayının yerini değiştirsek bile toplama işleminin sonucu değişmez.

Matematiksel gösterimi:

📌 Örnekler:

• (+8) + (-3) = +5
• (-3) + (+8) = +5
• (-6) + (+2) = (-4)
• (+2) + (-6) = (-4)

Her iki durumda da sonuç değişmediği için toplama işlemi değişme özelliğine sahiptir.

3. Birleşme (Gruplama) Özelliği

Üç veya daha fazla tam sayı toplarken, hangi ikisini önce topladığımız önemli değildir. Parantezlerin yerini değiştirebiliriz.

Matematiksel gösterimi:

📌 Örnekler:

• (2 + 3) + 4 = 2 + (3 + 4)
  • (5) + 4 = 2 + (7)
  • 9 = 9 ✅
• (-5 + 6) + (-3) = -5 + (6 + (-3))
  • 1 + (-3) = -5 + 3
  • -2 = -2 ✅

Bu özellik, büyük sayılarla işlem yaparken işlemi kolaylaştırır.

4. Etkisiz Eleman (Toplamaya Göre Birim Eleman) Özelliği

Bir sayıyı toplama işleminde etkisiz bırakabilen bir eleman vardır. Bu eleman 0’dır.

Matematiksel gösterimi:

📌 Örnekler:

• 7 + 0 = 7
• -12 + 0 = -12
• 0 + (-4) = -4

Bu yüzden 0, toplama işleminin etkisiz elemanıdır.

Özet

Tam sayılarla toplama işlemi şu 4 temel özelliğe sahiptir:
✅ Kapalılık: İki tam sayı toplandığında sonuç yine tam sayıdır.
✅ Değişme: Sayıların yeri değişse bile toplam değişmez.
✅ Birleşme: Parantezin yerini değiştirmek sonucu değiştirmez.
✅ Etkisiz Eleman: 0, toplamı değiştirmez.

Örnek Problemler

📌 Örnek 1:
Aşağıdaki işlemlerden hangisi birleşme özelliğini göstermektedir?
A) (-2 + 4) + 5 = -2 + (4 + 5)
B) (-3) + (-7) = -10
C) 9 + 0 = 9
D) 5 + (-2) = (-2) + 5

✅ Çözüm:
A şıkkı birleşme özelliğini göstermektedir çünkü parantezlerin yeri değiştirilmiştir.

📌 Örnek 2:
Bir bankadaki işlemlerde şu eşitlik veriliyor:
(-8) + 3 = 3 + (-8)
Bu eşitlik hangi özelliğe örnektir?

✅ Çözüm:
Bu, toplama işleminin değişme özelliğidir.

Tam Sayılarla Çarpma ve Bölme İşlemleri

Tam sayılarla çarpma ve bölme işlemleri, toplama ve çıkarma işlemlerinden farklı bazı kurallara sahiptir. Bu kuralların temelinde sayıların işaretleri bulunur. Çarpma ve bölme işlemlerinde sayının işareti sonucu doğrudan etkileyen en önemli faktördür.

Tam sayılarla çarpma ve bölme işlemlerinde şu kurallar geçerlidir:

1. Aynı işaretli iki tam sayının çarpımı ve bölümü pozitiftir.
2. Farklı işaretli iki tam sayının çarpımı ve bölümü negatiftir.

Şimdi bu kuralları detaylı inceleyelim.

1. Tam Sayılarla Çarpma İşlemi

a) Aynı İşaretli Sayıların Çarpımı

• İki pozitif tam sayının çarpımı pozitif olur.
  • (+4) × (+5) = +20
• İki negatif tam sayının çarpımı da pozitif olur.
  • (-3) × (-6) = +18

✔ Kural: Pozitif × Pozitif = Pozitif
✔ Kural: Negatif × Negatif = Pozitif

b) Farklı İşaretli Sayıların Çarpımı

• Bir pozitif ve bir negatif tam sayının çarpımı negatif olur.
  • (+7) × (-2) = -14
  • (-8) × (+3) = -24

✔ Kural: Pozitif × Negatif = Negatif
✔ Kural: Negatif × Pozitif = Negatif

📌 Örnek:
Bir mağazada fiyatı 15 TL olan bir ürün indirime girerek fiyatı -15 TL olarak gösteriliyor. Bir müşteri bu üründen 4 tane alıyor. Ödediği toplam ücret nedir?

✅ Çözüm:
(+4) × (-15) = -60 TL (Yani müşteri 60 TL ödeme yapar.)

2. Tam Sayılarla Bölme İşlemi

Bölme işlemi, çarpma işlemiyle aynı işaret kurallarına sahiptir.

a) Aynı İşaretli Sayıların Bölümü

• İki pozitif tam sayının bölümü pozitif olur.
  • (+18) ÷ (+3) = +6
• İki negatif tam sayının bölümü de pozitif olur.
  • (-24) ÷ (-6) = +4

✔ Kural: Pozitif ÷ Pozitif = Pozitif
✔ Kural: Negatif ÷ Negatif = Pozitif

b) Farklı İşaretli Sayıların Bölümü

• Bir pozitif ve bir negatif tam sayının bölümü negatif olur.
  • (+30) ÷ (-5) = -6
  • (-40) ÷ (+8) = -5

✔ Kural: Pozitif ÷ Negatif = Negatif
✔ Kural: Negatif ÷ Pozitif = Negatif

📌 Örnek:
Bir dalgıç, her dakika 4 metre derine inmektedir. 6 dakika sonra toplam kaç metre derine inmiştir?

✅ Çözüm:
(-4) × 6 = -24 metre (Dalgıç 24 metre derinliğe ulaşmıştır.)

Çarpma ve Bölme İşaret Kuralları

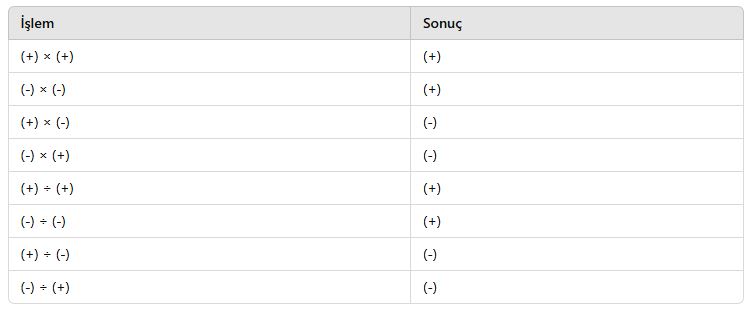
Örnek Problemler

📌 Örnek 1:
Aşağıdaki işlemleri yapınız.

a) (-6) × (+7) = ?
b) (-8) ÷ (-2) = ?
c) (+5) × (-4) = ?
d) (-18) ÷ (+6) = ?

✅ Çözüm:
a) (-6) × (+7) = -42
b) (-8) ÷ (-2) = +4
c) (+5) × (-4) = -20
d) (-18) ÷ (+6) = -3

📌 Örnek 2:
Bir uçak, 200 metre yükseklikten her saniye 50 metre yükselmektedir. 5 saniye sonra uçağın yeni yüksekliği ne olur?

✅ Çözüm:
Başlangıç yüksekliği: +200 m
Her saniye yükselme miktarı: +50 m
Toplam değişim: 50 × 5 = +250 m
Yeni yükseklik: 200 + 250 = 450 metre

Tam Sayıların Kendisi ile Tekrarlı Çarpımı (Üslü İfadeler)

Matematikte bazı işlemleri kısa ve pratik bir şekilde yazmak için üslü ifadeler kullanılır. Özellikle bir sayının kendisiyle tekrar tekrar çarpılması gerektiğinde üslü ifadeler büyük kolaylık sağlar.

Örneğin:

şeklinde yazmak yerine, bunu üslü ifade olarak

şeklinde gösterebiliriz.

Üslü ifadeler, özellikle büyük sayıların hesaplanmasını ve gösterilmesini kolaylaştırır. Şimdi üslü sayıların tanımını ve kurallarını inceleyelim.

1. Üslü İfadelerin Tanımı

Bir sayının kendisiyle n defa çarpılmasını göstermek için üslü ifadeler kullanılır.

Genel gösterimi:

Burada:

• a: Taban (tekrar çarpılan sayı)
• n: Üs (kaç defa çarpılacağını gösterir)
• a^n: Üslü ifade

📌 Örnekler:

• (+2)^3 = (+2) × (+2) × (+2) = +8
• (-5)^2 = (-5) × (-5) = +25
• (-4)^3 = (-4) × (-4) × (-4) = -64

2. Üslü Sayılarda İşaret Kuralları

Üssün çift veya tek olması, sonucun işaretini etkiler.

✔ Çift üslü negatif sayılar pozitif olur:

• (-3)^2 = (-3) × (-3) = +9
• (-2)^4 = (-2) × (-2) × (-2) × (-2) = +16

✔ Tek üslü negatif sayılar negatif olur:

• (-3)^3 = (-3) × (-3) × (-3) = -27
• (-2)^5 = (-2) × (-2) × (-2) × (-2) × (-2) = -32

✔ Pozitif tam sayılarda üs ne olursa olsun sonuç pozitiftir:

• (+4)^3 = (+4) × (+4) × (+4) = +64
• (+2)^6 = (+2) × (+2) × (+2) × (+2) × (+2) × (+2) = +64

📌 Örnek:
Hangisinin sonucu negatiftir?
A) (-2)^4
B) (-3)^3
C) (-5)^2
D) (-6)^6

✅ Çözüm:
(-3)^3 tek üslü olduğu için negatif olur. Cevap B şıkkıdır.

3. Üslü Sayılarla İşlem Kuralları

Üslü sayılarla işlem yaparken bazı temel kurallar kullanılır.

1️⃣ Çarpma Kuralı:
Tabanlar aynı ise üssler toplanır.

📌 Örnek:

2️⃣ Bölme Kuralı:
Tabanlar aynı ise üssler çıkartılır.

📌 Örnek:

3️⃣ Parantez Kuralı:
Üst üsteyse üsler çarpılır.

📌 Örnek:

4️⃣ Sıfır Üssü Kuralı:
Bir sayının sıfırıncı kuvveti her zaman 1’dir.

📌 Örnek:

5️⃣ Negatif Üs Kuralı:
Negatif üs, sayının tersini almak anlamına gelir.

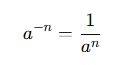
📌 Örnek:

Örnek Problemler

• Üslü ifadeler bir sayının tekrarlı çarpımını gösterir.
• Negatif sayıların çift üslü kuvvetleri pozitif, tek üslü kuvvetleri negatiftir.
• Üslü sayılarla çarpma ve bölmede üsler toplanır veya çıkarılır.
• Sıfır üssü her zaman 1’dir.
• Negatif üs, sayının tersini almayı ifade eder.

Tam Sayılarla İşlem Yapmayı Gerektiren Problemler

Tam sayılar günlük hayatta birçok alanda karşımıza çıkar. Sıcaklık değişimleri, banka hesapları, deniz seviyeleri, yükseklik farkları, kar-zarar hesaplamaları gibi birçok problem tam sayılar kullanılarak çözülür. Bu bölümde, tam sayılarla işlemleri gerektiren problem türlerini inceleyip, örnek çözümler yapacağız.

1. Günlük Hayatta Tam Sayılarla Problemler

📌 Örnek 1: Sıcaklık Değişimi
Bir şehirde sabah hava sıcaklığı -5°C idi. Gün içinde sıcaklık 7°C yükseldi. Akşam ise sıcaklık tekrar 4°C düştü. Akşam saatlerindeki hava sıcaklığı kaç derece olur?

✅ Çözüm:
Başlangıç sıcaklığı: -5°C
Gün içinde yükselme: +7°C
Akşam düşme: -4°C

İşlem:

Cevap: Akşam hava sıcaklığı -2°C olur.

📌 Örnek 2: Banka Hesap İşlemi
Ahmet’in banka hesabında -120 TL borcu vardı. Hesabına 300 TL yatırdı. Daha sonra 150 TL çekti. Ahmet’in banka hesabındaki yeni bakiyesi kaç TL olur?

✅ Çözüm:
Başlangıç borç: -120 TL
Para yatırma: +300 TL
Para çekme: -150 TL

İşlem:

Cevap: Ahmet’in banka hesabında 30 TL kalmıştır.

2. Tam Sayılarla Çarpma ve Bölme Problemleri

📌 Örnek 3: Çarpma İşlemi ile Problem Çözme
Bir dalgıç, her dakika -4 metre derine inmektedir. 6 dakika sonra kaç metre derine inmiş olur?

✅ Çözüm:
Her dakika inme: -4 metre
Toplam süre: 6 dakika

İşlem:

Cevap: Dalgıç 24 metre derine inmiştir.

📌 Örnek 4: Bölme İşlemi ile Problem Çözme
Bir yük asansörü -30 metre aşağı inerek bodrum katına ulaşıyor. Asansör her katta -5 metre alçalıyor. Asansör kaç kat aşağı inmiştir?

✅ Çözüm:
Toplam mesafe: -30 metre
Her katın mesafesi: -5 metre

İşlem:

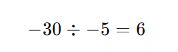
Cevap: Asansör 6 kat aşağı inmiştir.

3. Kar ve Zarar Hesaplamaları

📌 Örnek 5: Bir Şirketin Kar-Zarar Hesabı
Bir şirket ilk çeyrekte +20.000 TL kar etti. İkinci çeyrekte -8.000 TL zarar etti. Üçüncü çeyrekte +15.000 TL kar etti. Son çeyrekte ise -10.000 TL zarar etti. Şirket yıl sonunda toplam ne kadar kar veya zarar etmiştir?

✅ Çözüm:
İlk çeyrek: +20.000 TL
İkinci çeyrek: -8.000 TL
Üçüncü çeyrek: +15.000 TL
Son çeyrek: -10.000 TL

İşlem:

Cevap: Şirket yıl sonunda 17.000 TL kar etmiştir.

📌 Örnek 6: Seyahat Hesaplaması
Bir otobüs, sabah +120 km ilerledi, öğleden sonra -80 km geri döndü, akşam ise tekrar +60 km ilerledi. Otobüsün net hareketi kaç km olmuştur?

✅ Çözüm:
İleri hareket: +120 km
Geri dönüş: -80 km
İleri hareket: +60 km

İşlem:

Cevap: Otobüs toplamda 100 km ilerlemiştir.

Özet

• Günlük hayatta sıcaklık değişimi, banka hesapları ve mesafe hesaplamalarında tam sayılar kullanılır.
• Çarpma işlemlerinde negatif sayılar yön değiştirir ve sayının büyüklüğünü artırır.
• Bölme işlemlerinde negatif sayılar yön değiştirir ve adım adım çözülmelidir.
• Kar-zarar hesaplamalarında işlemler dikkatlice yapılmalıdır.

📌 Ödev:
Aşağıdaki problemleri çözünüz:

1. Bir hava balonu -10 metre alçaldı, ardından +15 metre yükseldi, sonra -5 metre alçaldı. Son yüksekliği kaç metredir?
2. Bir fabrika bir gün boyunca 3 vardiya çalışıyor. Sabah vardiyası +120 adet ürün üretti, öğlen vardiyası -50 adet hata yaptı, akşam vardiyası +90 adet ürün üretti. Toplam kaç ürün üretilmiştir?
3. (-4) × (-3) × 2 işleminin sonucu nedir?

Tam Sayılarla İşlemler – 10 Soruluk Test

1. Aşağıdaki işlemlerden hangisinin sonucu negatiftir?

A) (-7) + (+3)
B) (-9) × (-2)
C) (-4) ÷ (+2)
D) (+5) × (+4)

2. (-6) + (+8) – (-3) işleminin sonucu kaçtır?

A) 1
B) 5
C) 7
D) 9

3. Aşağıdaki işlemlerden hangisi doğrudur?

A) (+3) + (-5) = -2
B) (-7) × (+3) = +21
C) (-12) ÷ (-4) = -3
D) (-6) – (-2) = -8

4. Bir mağazada fiyatı 120 TL olan bir ürün indirime girerek -40 TL daha ucuzladı. Ürünün yeni fiyatı kaç TL oldu?

A) 80
B) 100
C) 60
D) 70

5. (-3)^4 işleminin sonucu kaçtır?

A) -81
B) 81
C) -27
D) 27

6. Aşağıdaki işlemlerden hangisi yanlıştır?

A) (-5) × (-4) = 20
B) (+6) ÷ (-2) = -3
C) (-10) + (+7) = -3
D) (-8) ÷ (-2) = -4

7. Bir otobüs sabah +80 km ilerledi, öğleden sonra -50 km geri döndü, akşam ise tekrar +40 km ilerledi. Otobüs toplam kaç km yol almıştır?

A) 70 km
B) 60 km
C) 90 km
D) 80 km

8. (-5) × (+3) × (-2) işleminin sonucu kaçtır?

A) 30
B) -30
C) -15
D) 15

9. 2^3 × 2^2 işleminin sonucu kaçtır?

A) 16
B) 8
C) 32
D) 64

10. Bir dalgıç her dakika -6 metre derine inmektedir. 5 dakika sonra kaç metre derinde olur?

A) -25
B) -30
C) -36
D) -40

Cevap Anahtarı

1 – C
2 – D
3 – A
4 – A
5 – B
6 – D
7 – A
8 – A
9 – C
10 – B