İçindekiler
Veri Analizi Konu Anlatımı
Veri analizi, toplanan bilgilerin düzenlenmesi, karşılaştırılması ve yorumlanması sürecidir. Günlük hayatta anketler, istatistikler, öğrenci başarı durumları, ekonomi ve sağlık alanında sıkça kullanılır.
Bu ünitede veri gruplarına ait çizgi grafikleri, ortalama ve medyan hesaplamaları, daire grafiği oluşturma ve grafiklerin uygunluğunu değerlendirme konularını ele alacağız.
Bir Veri Grubuna Ait Çizgi Grafiği
✔ Çizgi grafiği, verilerin zaman içindeki değişimini göstermek için kullanılan bir grafik türüdür.
✔ Özellikleri:
- Veriler bir noktalar halinde gösterilir ve bu noktalar birleştirilerek çizgi oluşturulur.
- Genellikle belirli zaman aralıklarında değişen veriler için uygundur (örneğin, hava durumu, hisse senedi değişimi, nüfus artışı).
📌 Örnek:
Bir okulda 5 gün boyunca satılan kitap sayıları şu şekildedir:

Bu verileri çizgi grafiğiyle göstermek için x eksenine günleri, y eksenine satılan kitap sayısını yerleştiririz ve noktaları birleştiririz.
✅ Yorum:
- En çok kitap Cuma günü satılmıştır.
- Satışlar genel olarak artış göstermiştir.
- Çarşamba ve Perşembe günleri arasında azalma olmuştur.
📌 Örnek Problemler:
- Bir öğrencinin 6 ay boyunca testlerde aldığı puanlar sırasıyla: 75, 80, 78, 85, 90, 95’tir. Bu veriler için çizgi grafiği çizin ve yorumlayın.
- Bir çiftlikte 5 gün boyunca toplanan yumurta sayıları: 20, 25, 22, 30, 28’dir. Çizgi grafiğini oluşturup verileri yorumlayınız.
- Bir mağazada satılan ürün sayısı 4 hafta boyunca: 150, 170, 160, 180’dir. Satış trendini açıklayın.
Bir Veri Grubuna Ait Ortalama, Ortanca ve Tepe Değer
Verileri anlamak ve yorumlamak için ortalama (aritmetik ortalama), ortanca (medyan) ve tepe değer (mod) gibi istatistiksel ölçüler kullanılır.
Aritmetik Ortalama (Ortalama)
✔ Tanım:
Bir veri grubundaki tüm değerlerin toplamının, veri sayısına bölünmesiyle elde edilir.
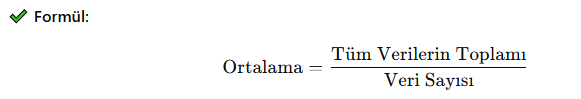
📌 Örnek 1:
Bir sınıftaki öğrencilerin sınav notları: 60, 70, 80, 90, 100
Bu notların ortalamasını bulun.

Ortanca (Medyan)
✔ Tanım:
Veriler küçükten büyüğe sıralandığında ortada kalan değerdir.
- Tek sayıda veri varsa: Ortadaki sayı medyandır.
- Çift sayıda veri varsa: Ortadaki iki sayının ortalaması alınır.
📌 Örnek 2:
Bir öğrencinin 6 sınavdan aldığı notlar: 50, 60, 70, 80, 90, 100
Ortanca değeri bulun.
✅ Çözüm:
Sıralanmış veri: 50, 60, 70, 80, 90, 100
Orta kısımdaki iki sayı: 70 ve 80

Tepe Değer (Mod)
✔ Tanım:
Bir veri grubunda en sık tekrar eden değer tepe değer (mod) olarak adlandırılır.
📌 Örnek 3:
Bir markette bir hafta boyunca satılan ekmek sayıları: 20, 22, 22, 24, 25, 26, 22
Tepe değer nedir?
✅ Çözüm:
En sık tekrar eden sayı 22’dir (3 kez tekrar ediyor).
✔ Sonuç: Tepe değer 22’dir.
📌 Örnek Problemler:
- Bir öğrencinin haftalık çalışma saatleri: 2, 4, 6, 8, 10’tur. Aritmetik ortalamayı bulun.
- Bir mağazada günlük satılan çikolata miktarları: 15, 18, 20, 25, 22, 20, 20’dir. Tepe değeri nedir?
- Bir öğrencinin 5 sınav notu: 70, 80, 90, 85, 75’tir. Ortanca değeri bulun.
- Bir grubun yaşları: 24, 26, 28, 22, 30, 26, 26’dır. Tepe değeri ve ortalamasını hesaplayınız.
- Bir okuldaki öğrenci sayıları: 200, 250, 300, 400, 350, 250, 250’dir. Hangi sayı tepe değerdir?
Bir Veri Grubuna Ait Daire Grafiği
Daire grafiği, bir veri grubundaki kategorilerin birbirine oranını ve dağılımını göstermek için kullanılan bir grafik türüdür. Veriler, bir daire içinde dilimler halinde gösterilir ve her dilim, verinin toplam içindeki yüzdesine göre belirlenir.
Daire Grafiği Nasıl Oluşturulur?
✔ Adımlar:
1. Toplam veri hesaplanır.
2. Her kategori için yüzde hesaplanır.

3. Dilim açısı hesaplanır.
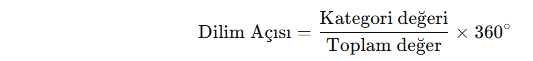
4. Daire grafiği çizilir ve bölümler etiketlenir.
Örnek: Daire Grafiği Hesaplama
📌 Örnek 1:
Bir okulda öğrencilerin seçtiği spor branşları şu şekildedir:
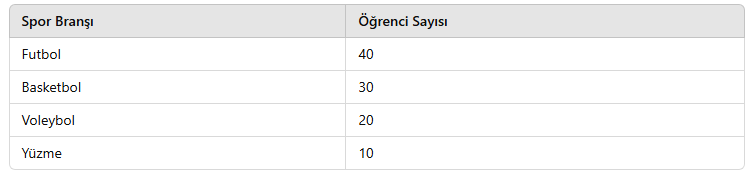

Daire Grafiği ile Veri Analizi
✔ Daire grafiği kullanımı için uygun durumlar:
- Oranların ve yüzdelerin gösterilmesi (örneğin, sınıftaki erkek-kız öğrenci oranı).
- Toplam içindeki farklı kategorilerin karşılaştırılması (örneğin, okul kantininde satılan ürünlerin dağılımı).
- Bütünün parçaları arasındaki ilişkilerin incelenmesi (örneğin, bir şirketin yıllık bütçesinin bölümlere dağılımı).
✔ Daire grafiği uygun olmayan durumlar:
- Zamanla değişen verileri göstermek için uygun değildir (çizgi grafiği daha uygundur).
- Çok sayıda kategori içeren verilerde karışıklığa neden olabilir.
📌 Örnek Problemler:
- Bir mağazada satılan ürünlerin dağılımı: Elektronik (50), Giyim (30), Kitap (20). Daire grafiğinde her kategorinin yüzdesini ve açılarını hesaplayınız.
- Bir okuldaki öğrencilerin seçtiği yabancı diller: İngilizce (80), Almanca (40), Fransızca (20). Daire grafiğini oluşturun.
- Bir belediye bütçesi şu şekilde dağıtılmıştır: Eğitim (%30), Sağlık (%25), Ulaşım (%20), Kültür (%15), Diğer (%10). Bu veriler için daire grafiği oluşturun.
- Bir şirketin yıllık satış gelirleri şu şekildedir: Türkiye (40 milyon), Avrupa (35 milyon), Asya (25 milyon). Daire grafiğinde her bölgenin yüzdesini ve açılarını hesaplayınız.
- Bir okulun kütüphanesindeki kitap türleri: Roman (120), Bilim (80), Tarih (60), Çocuk (40). Daire grafiği için her türün yüzdesini ve açısını hesaplayınız.
Verilerin Uygunluğuna Göre Grafik Çeşitleri
Verileri daha iyi analiz edebilmek için farklı grafik türleri kullanılır. Hangi grafiğin kullanılacağı, verinin türüne ve nasıl sunulması gerektiğine bağlıdır.
Bu bölümde, çizgi, sütun, daire ve histogram grafikleri arasındaki farkları ve hangi durumlarda kullanılmaları gerektiğini inceleyeceğiz.
1. Grafik Türleri ve Kullanım Alanları
✔ 1. Çizgi Grafiği
- Kullanım Alanı: Zaman içindeki değişimleri göstermek için uygundur.
- Örnek: Hava sıcaklığının günlere göre değişimi, hisse senedi fiyatları, öğrenci başarı grafiği.
📌 Örnek:
Bir öğrencinin aylık test sonuçları şu şekildedir:
- Ocak: 70
- Şubat: 75
- Mart: 80
- Nisan: 85
- Mayıs: 90
✔ Bu veri, çizgi grafiğiyle gösterildiğinde başarı trendi anlaşılır.
✔ 2. Sütun (Çubuk) Grafiği
- Kullanım Alanı: Farklı kategorilere ait değerleri karşılaştırmak için uygundur.
- Örnek: Bir mağazadaki ürün satışları, spor branşlarının popülerliği, okulda seçilen derslerin oranı.
📌 Örnek:
Bir okulda öğrencilerin seçtiği branşlar:
- Futbol: 50 öğrenci
- Basketbol: 40 öğrenci
- Voleybol: 30 öğrenci
- Masa Tenisi: 20 öğrenci
✔ Bu veriler, sütun grafiği ile net bir şekilde karşılaştırılabilir.
✔ 3. Daire Grafiği
- Kullanım Alanı: Bir bütünün parçalarını ve oranlarını göstermek için uygundur.
- Örnek: Okul kantininde satılan ürünlerin yüzdelik dağılımı, bir şirketin gelir dağılımı, şehirlerde nüfus oranları.
📌 Örnek:
Bir okulun kütüphanesindeki kitap türleri:
- Roman: %40
- Bilim: %30
- Tarih: %20
- Çocuk: %10
✔ Daire grafiği, oranların karşılaştırılmasını kolaylaştırır.
✔ 4. Histogram Grafiği
- Kullanım Alanı: Büyük veri gruplarında verinin dağılımını göstermek için uygundur.
- Örnek: Sınav notlarının dağılımı, yaş gruplarına göre nüfus dağılımı, fabrika üretim hatalarına göre frekans analizi.
📌 Örnek:
Bir sınıftaki öğrencilerin sınav notları şu şekildedir:
- 0-20 arası: 5 öğrenci
- 21-40 arası: 8 öğrenci
- 41-60 arası: 12 öğrenci
- 61-80 arası: 10 öğrenci
- 81-100 arası: 7 öğrenci
✔ Histogram, verilerin belirli aralıklara (sıklık gruplarına) nasıl dağıldığını gösterir.
Hangi Grafik Ne Zaman Kullanılmalı?

📌 Örnek Problemler:
- Bir şirketin yıllık satışları 5 yıl boyunca artmıştır. Bu veriyi hangi grafik türü ile göstermeliyiz?
- Bir okulda en çok tercih edilen dersleri karşılaştırmak için hangi grafik uygundur?
- Bir kütüphanedeki kitap türlerinin oranlarını göstermek için hangi grafik kullanılır?
- Bir markette haftalık satılan ürünlerin değişimini incelemek için hangi grafik uygundur?
- Bir fabrikada üretilen ürünlerin hatalı çıkma sıklığını göstermek için hangi grafik daha uygundur?
Veri Analizi – 10 Soruluk Test
1.
Bir öğrenci, yıl boyunca girdiği deneme sınavlarındaki başarı grafiğini oluşturmak istiyor. Hangi grafik türünü kullanmalıdır?
A) Sütun grafiği
B) Daire grafiği
C) Çizgi grafiği
D) Histogram
2.
Bir okulda öğrencilerin tercih ettiği dersler şu şekildedir:
Matematik: 40 öğrenci
Fen Bilimleri: 30 öğrenci
Sosyal Bilgiler: 20 öğrenci
Türkçe: 10 öğrenci
Bu verileri en iyi hangi grafik türüyle gösterebiliriz?
A) Çizgi grafiği
B) Histogram
C) Sütun grafiği
D) Daire grafiği
3.
Bir okul kantininde satılan ürünlerin yüzdelik dağılımını göstermek için hangi grafik türü en uygundur?
A) Çizgi grafiği
B) Daire grafiği
C) Histogram
D) Sütun grafiği
4.
Bir mağazada satılan ayakkabı sayıları şu şekildedir:
Ocak: 200
Şubat: 250
Mart: 230
Nisan: 280
Mayıs: 300
Bu verilere göre en uygun grafik türü hangisidir?
A) Çizgi grafiği
B) Histogram
C) Sütun grafiği
D) Daire grafiği
5.
Bir öğrencinin haftalık çalışma saatleri şu şekildedir: 5, 7, 8, 6, 7, 10, 5.
Bu verinin aritmetik ortalaması kaçtır?
A) 6.75
B) 7
C) 7.14
D) 7.25
6.
Bir sınavda öğrencilerin aldığı notlar: 50, 60, 70, 80, 90, 100.
Bu veri grubunun ortanca (medyan) değeri kaçtır?
A) 70
B) 75
C) 80
D) 85
7.
Bir markette satılan çikolata miktarları şu şekildedir: 15, 18, 20, 25, 22, 20, 20.
Bu veri grubunun tepe değeri (mod) kaçtır?
A) 15
B) 18
C) 20
D) 25
8.
Bir sınıfta öğrencilerin yaş dağılımı şu şekildedir:
10 yaş: 5 öğrenci
11 yaş: 8 öğrenci
12 yaş: 12 öğrenci
13 yaş: 10 öğrenci
14 yaş: 7 öğrenci
Bu verileri göstermek için en uygun grafik türü hangisidir?
A) Çizgi grafiği
B) Histogram
C) Sütun grafiği
D) Daire grafiği
9.
Bir sınıftaki 40 öğrencinin spor branşı tercihleri şu şekildedir:
Futbol: 12
Basketbol: 10
Voleybol: 8
Yüzme: 10
Daire grafiği çizmek için basketbol kategorisinin açısı kaç derece olmalıdır?
A) 72°
B) 80°
C) 90°
D) 100°
10.
Bir şehirde aylık sıcaklık değişimleri aşağıdaki gibidir:
Ocak: 5°C
Şubat: 7°C
Mart: 12°C
Nisan: 18°C
Mayıs: 22°C
Bu verilere göre en uygun grafik türü hangisidir?
A) Çizgi grafiği
B) Histogram
C) Sütun grafiği
D) Daire grafiği
Cevap Anahtarı
1 – C
2 – C
3 – B
4 – A
5 – C
6 – B
7 – C
8 – B
9 – A
10 – A
