Basit Olayların Olma Olasılığı

Olasılık, bir olayın gerçekleşme ihtimalini ölçen matematiksel bir kavramdır. Günlük hayatta birçok durumda şans, rastgelelik ve olasılık hesaplamaları ile karşılaşırız. Örneğin, zar attığımızda 6 gelme ihtimali, bir madeni paranın yazı veya tura gelme olasılığı gibi durumlar basit olasılık hesaplarına örnektir.

Basit olayların olasılığı, tek bir olayın gerçekleşme ihtimalini ifade eder. Bir olayın olasılığı, istenen durum sayısının tüm olası durumlara bölünmesiyle hesaplanır. Matematiksel olarak:

Bu formül, eşit olasılıklı durumlar için geçerlidir ve 0 ile 1 arasında bir değer alır. 0 olasılığı olan bir olay imkânsızdır, 1 olasılığı olan bir olay ise kesin olarak gerçekleşir. Şimdi basit olayların olasılığıyla ilgili detaylara geçelim. 🚀

8. Sınıf Matematik Basit Olayların Olma Olasılığı Konu Anlatımı

Olasılık, bir olayın gerçekleşme ihtimalini ölçen matematiksel bir kavramdır. Bir olayın olasılığı 0 ile 1 arasında bir değer alır:

• 0 → İmkânsız olay (Gerçekleşmesi mümkün değil).
• 1 → Kesin olay (Mutlaka gerçekleşir).
• 0 ile 1 arasındaki değerler → Olasılığı değişken olaylar.

Matematikte olasılık hesaplamaları için şu formül kullanılır:

Burada:

• P(A) → A olayının gerçekleşme olasılığıdır.
• İstenen olay sayısı, gerçekleşmesi beklenen durumları ifade eder.
• Tüm olası durumların sayısı, deneyde ortaya çıkabilecek tüm farklı sonuçlardır.

1. Madeni Para Atma Olasılığı

Bir madeni para yazı (Y) veya tura (T) gelebilir. Olasılık hesaplaması:

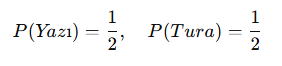
✅ Örnek:
Bir madeni para 5 defa atıldığında her seferinde yazı gelme olasılığı yine 1/2’dir. Önceki atışlar sonucu değiştirmez.

📌 Sonuç: Madeni para adil bir şekilde atıldığında, yazı veya tura gelme olasılığı her zaman eşittir (1/2).

2. Zar Atma Olasılığı

Bir zarın 6 yüzeyi vardır: 1, 2, 3, 4, 5, 6. Her yüzün gelme olasılığı eşittir:

✅ Örnekler:

Bir zarda 4 gelme olasılığı:

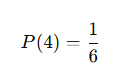
Tek sayı gelme olasılığı: (1, 3, 5)

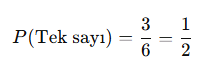
Çift sayı gelme olasılığı: (2, 4, 6)

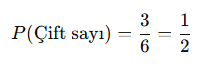
📌 Sonuç: Her yüz eşit ihtimalle geleceğinden, zar oyunlarında olasılık hesaplamaları adil şekilde yapılabilir.

3. Deste Kart Çekme Olasılığı

Bir iskambil destesindeki kartların dağılımı:

• 52 kart
• 4 farklı renk (Kupa, Maça, Sinek, Karo)
• Her renkte 13 kart
• 2 renk (Kırmızı: Kupa ve Karo, Siyah: Maça ve Sinek)

✅ Örnekler:

Kupa çekme olasılığı:

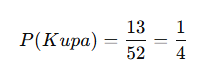
As çekme olasılığı: (Dört As var)

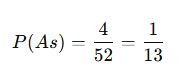
Siyah kart çekme olasılığı:

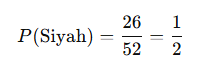
📌 Sonuç: Kart oyunlarında olasılık, hangi kart grubunun çekildiğine bağlı olarak değişir.

4. Olasılıkta İmkânsız ve Kesin Olaylar

Bazı olaylar hiç gerçekleşemezken (olasılığı 0), bazı olaylar mutlaka gerçekleşir (olasılığı 1).

✅ Örnekler:

📌 Sonuç: Bazı olaylar imkânsızdır (olasılık 0), bazı olaylar ise kesin gerçekleşir (olasılık 1).

5. Gerçek Hayatta Olasılık Kullanımı

✔ Hava durumu tahmini:

• %80 yağmur ihtimali → Yağmur olasılığı 0,8
• %20 güneşli hava ihtimali → Güneş olasılığı 0,2

✔ Spor bahisleri:

• Bir takımın kazanma olasılığı hesaplanır.

✔ Sağlık ve tıp:

• Bir hastalığa yakalanma olasılığı belirlenir.

✅ Örnek:
Bir hastalığın görülme ihtimali %5 ise:

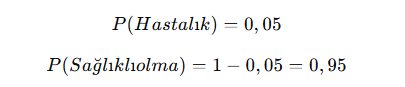
📌 Sonuç: Olasılık, günlük yaşamda birçok alanda kullanılan önemli bir kavramdır.

📌 Bu konuda öğrendiklerimiz:
✅ Olasılığın temel formülünü öğrendik.
✅ Madeni para, zar ve kart çekme olasılıklarını hesapladık.
✅ İmkânsız ve kesin olay kavramlarını inceledik.
✅ Gerçek hayatta olasılığın nasıl kullanıldığını gördük.

Deneysel ve Teorik Olasılık

Olasılık hesaplamaları iki farklı şekilde ele alınır:
1️⃣ Teorik Olasılık: Olayların olasılığını matematiksel olarak hesaplama yöntemi.
2️⃣ Deneysel Olasılık: Olasılığı deneyler ve gözlemler sonucunda belirleme yöntemi.

Bu bölümde teorik ve deneysel olasılık arasındaki farkları ve nasıl hesaplandıklarını detaylıca inceleyeceğiz.

1. Teorik Olasılık Nedir?

📌 Tanım:
Bir olayın tüm olası durumlara göre matematiksel olarak hesaplanan olasılığıdır.

Teorik olasılık formülü:

✅ Örnek 1 – Zar Atma:
Bir zarın 6 yüzü olduğu için, her yüz gelme olasılığı eşittir.

Bir zarın 4 gelme olasılığı:

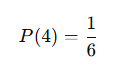
Tek sayı gelme olasılığı: (1, 3, 5)

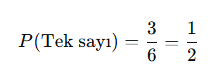
✅ Örnek 2 – Madeni Para:
Bir madeni para adil bir şekilde atıldığında, yazı veya tura gelme olasılığı:

📌 Sonuç: Teorik olasılık, olayların matematiksel olarak hesaplanan ihtimalleridir.

2. Deneysel Olasılık Nedir?

📌 Tanım:
Bir olayın gerçek deneylerde kaç kez gerçekleştiğine bağlı olarak hesaplanan olasılıktır.

Deneysel olasılık formülü:

✅ Örnek 1 – Madeni Para Atma:

• Bir madeni para 100 defa atılıyor.
• 55 kez yazı, 45 kez tura geliyor.
• Deneysel olasılık:

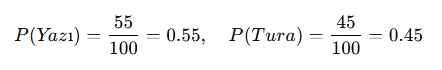
📌 Sonuç: Deneysel olasılık, teorik olasılıktan farklı olabilir, çünkü rastgele olaylarda küçük farklar oluşabilir.

✅ Örnek 2 – Zar Atma:

• Bir zar 60 defa atılıyor.
• 10 kez 6 geliyor.
• Deneysel olasılık:

📌 Sonuç: Deney sayısı arttıkça, deneysel olasılık teorik olasılığa daha çok yaklaşır.

3. Teorik ve Deneysel Olasılık Arasındaki Farklar

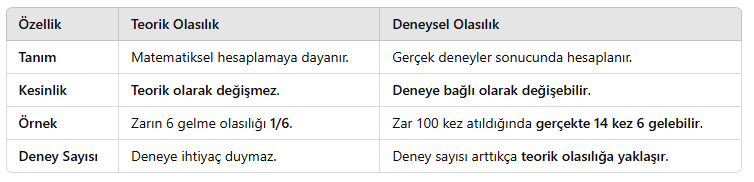
4. Deney Sayısı Artarsa Ne Olur?

✔ Deney sayısı azsa, deneysel olasılık değişken olabilir.
✔ Deney sayısı arttıkça, deneysel olasılık teorik olasılığa yaklaşır.

✅ Örnek:

• Bir madeni para 10 defa atılırsa: Yazı 7, tura 3 gelebilir.
• Bir madeni para 1000 defa atılırsa: Yazı ve tura yaklaşık %50’ye yaklaşır.

📌 Sonuç: Deney sayısı arttıkça, gerçek sonuçlar teorik olasılığa daha çok yaklaşır.

5. Gerçek Hayatta Teorik ve Deneysel Olasılık Kullanımı

✔ Hava durumu tahmini:

• Teorik Olasılık: Mevsimsel verilerle tahmin yapılır.
• Deneysel Olasılık: Önceki yılların verileri incelenir.

✔ Spor istatistikleri:

• Futbolcuların penaltı gol yüzdeleri hesaplanır.
• Örneğin, bir futbolcu 50 penaltıdan 40’ını gol yaparsa:

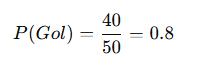
Trafik kazası tahminleri:

• Kavşaklarda geçmiş verilere göre kaza olasılığı hesaplanır.

📌 Bu konuda öğrendiklerimiz:
✅ Teorik olasılığı nasıl hesaplayacağımızı öğrendik.
✅ Deneysel olasılığın nasıl farklı olabileceğini inceledik.
✅ Teorik ve deneysel olasılık arasındaki farkları gördük.
✅ Gerçek hayatta olasılığın nasıl kullanıldığını öğrendik.

Birleşik Olayların Olasılığı

Bazı olaylar tek bir durumdan oluşurken (basit olaylar), bazı olaylar birden fazla olayın birleşmesiyle meydana gelir. Birleşik olayların olasılığı, bu olayların birlikte gerçekleşme durumlarına göre hesaplanır.

Bu bölümde bağımsız ve bağımlı olaylar, ve ve veya olayları, olası sonuçları hesaplama yöntemleri gibi konuları detaylı şekilde inceleyeceğiz.

1. Birleşik Olay Nedir?

📌 Tanım:
Birleşik olaylar, birden fazla olayın aynı anda gerçekleşmesi veya bir olayın farklı seçeneklerle ortaya çıkması durumudur.

Birleşik olaylar genellikle iki gruba ayrılır:
1️⃣ Bağımsız Olaylar: Bir olayın gerçekleşmesi, diğer olayın sonucunu etkilemez.
2️⃣ Bağımlı Olaylar: Bir olayın gerçekleşmesi, diğer olayın sonucunu değiştirir.

2. Bağımsız Olayların Olasılığı

📌 Tanım:
İki olay birbirinden bağımsızsa, birinin gerçekleşmesi diğerinin sonucunu etkilemez.

✅ Örnek:

• Bir madeni para atılır ve bir zar atılır.
• Madeni paranın yazı gelmesi, zarın 6 gelmesini etkilemez.

Bağımsız olayların olasılığı şu şekilde hesaplanır:

📌 Sonuç: Bağımsız olayların olasılığı, ayrı ayrı olasılıklarının çarpımıdır.

3. Bağımlı Olayların Olasılığı

📌 Tanım:
Bağımlı olaylarda, bir olayın gerçekleşmesi diğer olayın olasılığını değiştirir.

✅ Örnek:

• Bir torbada 5 kırmızı ve 3 mavi top var.
• Birinci çekilen topun rengi, ikinci çekilen topun olasılığını değiştirir.

Bağımlı olayların olasılığı şu formülle hesaplanır:

📌 Örnek:

• Bir torbada 4 yeşil ve 6 kırmızı top var.
• İlk çekilen topun kırmızı olma olasılığı:

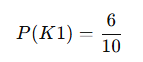
İlk top çekildikten sonra geri koyulmazsa, ikinci kırmızı topun çekilme olasılığı:

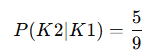
İki topun da kırmızı olma olasılığı:

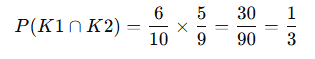
📌 Sonuç: Bağımlı olaylarda, ilk olayın sonucu ikinci olayın olasılığını değiştirir.

4. VE ve VEYA Olayları

Olasılıkta “ve” ve “veya” olayları hesaplanırken farklı yöntemler kullanılır.

✔ “VE” Olayı (Kesişim – ∩):

• İki olayın aynı anda gerçekleşme olasılığı hesaplanırken çarpma kuralı kullanılır.

✅ Örnek:
Bir torbada 4 kırmızı, 3 mavi, 5 sarı top var.

• Kırmızı veya mavi top çekme olasılığı:

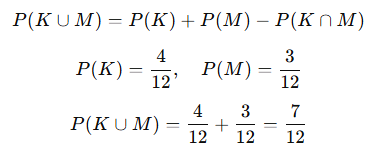
📌 Sonuç: VEYA olaylarında, iki olasılık toplanır ancak ortak olanlar çıkarılır.

5. Gerçek Hayatta Birleşik Olayların Olasılığı

✔ Trafik Kazaları:

• Bir şehirde yağmurlu günlerde kazaların artma olasılığı hesaplanabilir.

✔ Sağlık İstatistikleri:

• Bir hastanın aynı anda iki farklı hastalığa yakalanma ihtimali hesaplanabilir.

✔ Spor Analizleri:

• Bir futbol maçında bir takımın hem kazanma hem de gol atma olasılığı hesaplanabilir.

✅ Örnek:
Bir futbol takımının galibiyet olasılığı %60, gol atma olasılığı %80.

• İkisinin aynı anda gerçekleşme olasılığı:

Sonuç: Takımın hem kazanıp hem gol atma olasılığı %48’dir.

📌 Bu konuda öğrendiklerimiz:
✅ Bağımsız olayların olasılığı çarpım kuralıyla hesaplanır.
✅ Bağımlı olaylarda bir olay diğerini etkiler.
✅ VE olaylarında çarpma, VEYA olaylarında toplama yapılır.
✅ Gerçek hayatta birleşik olayların nasıl hesaplandığını inceledik.

8. Sınıf Matematik Basit Olayların Olma Olasılığı Örnek Sorular

1. Bağımsız Olayların Olasılığı

📌 Soru 1:
Bir madeni para ve bir zar aynı anda atılıyor.

• Madeni paranın yazı gelme olasılığı 1/2
• Zarın 4 gelme olasılığı 1/6
  Bu iki olayın aynı anda gerçekleşme olasılığı nedir?

Çözüm:
Bağımsız olaylarda olasılıklar çarpılır:

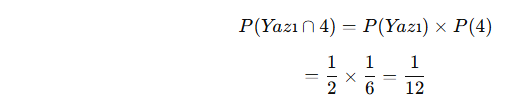
✅ Cevap: 1/12

2. Bağımlı Olayların Olasılığı

📌 Soru 2:
Bir torbada 5 kırmızı, 3 mavi top vardır.

• İlk çekilen top geri koyulmadan ikinci top çekildiğinde,
• İlk topun kırmızı, ikinci topun da kırmızı olma olasılığı nedir?

Çözüm:

• İlk kırmızı top çekme olasılığı:

✅ Cevap: 5/14

3. VE Olayı (Kesişim – ∩) Hesaplama

📌 Soru 3:
Bir okulda yapılan ankette öğrencilerin %40’ı basketbol, %30’u futbol, %20’si hem basketbol hem futbol seviyor.
Bir öğrencinin hem basketbol hem de futbol sevme olasılığı nedir?

Çözüm:

✅ Cevap: %20

4. VEYA Olayı (Birimleşim – ∪) Hesaplama

📌 Soru 4:
Bir torbada 4 kırmızı, 6 mavi, 5 sarı top vardır.
Bir top çekildiğinde kırmızı veya mavi gelme olasılığı nedir?

Çözüm:

✅ Cevap: 2/3

5. Kart Çekme Olasılığı

📌 Soru 5:
Bir iskambil destesinden kupa veya as çekme olasılığı nedir?

Çözüm:

• Toplam 52 kart vardır.
• Kupa kartları = 13, As kartları = 4
• Kupa ası ortak olduğu için 1 kez çıkarılmalıdır.

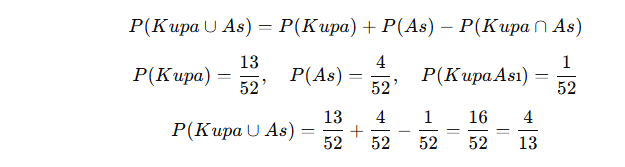
✅ Cevap: 4/13

6. Zar ve Çark Problemi

📌 Soru 6:
Bir zar ve 5 bölmeli bir çark aynı anda atılıyor.

• Zarın 2 gelme olasılığı: 1/6
• Çarkın B bölgesine gelme olasılığı: 1/5
  Bu iki olayın aynı anda gerçekleşme olasılığı nedir?

Çözüm:
Bağımsız olaylarda olasılıklar çarpılır:

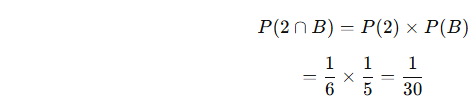
✅ Cevap: 1/30

7. Torbadan Top Çekme (Bağımlı Olay)

📌 Soru 7:
Bir torbada 3 beyaz, 4 siyah, 5 kırmızı top vardır.

• İlk çekilen top beyaz, ikinci çekilen top da beyaz olursa olasılık nedir?
• Çekilen top geri konmaz.

Çözüm:

• İlk beyaz top çekme olasılığı:

✅ Cevap: 1/22

8. VEYA Olasılığı ile Hesaplama

📌 Soru 8:
Bir okulda öğrencilerin %50’si matematiği, %40’ı fen bilimlerini sever.

• %20’si hem matematik hem fen seviyor.
• Bir öğrencinin en az birini sevme olasılığı nedir?

Çözüm:
VEYA kuralı kullanılır:

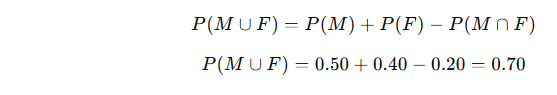
✅ Cevap: %70

9. Çekiliş Problemi

📌 Soru 9:
Bir kutuda 10 kırmızı, 8 mavi, 7 yeşil bilye var.

• Birinci çekilen bilyenin kırmızı, ikinci çekilen bilyenin mavi olma olasılığı nedir?
• Çekilen bilyeler yerine konmaz.

Çözüm:

• İlk kırmızı çekme olasılığı:

✅ Cevap: 2/15

10. Trafik Kazası Olasılığı

📌 Soru 10:
Bir şehirde yağmurlu günlerde kaza olasılığı %30, yağmur olasılığı %40’tır.

• Bir günün hem yağmurlu hem de kazalı olma olasılığı nedir?

Çözüm:
Bağımlı olay olarak hesaplanır:

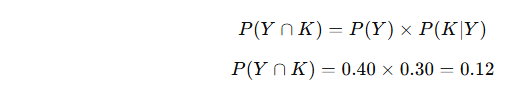
✅ Cevap: %12

📌 Bu 10 soru ile şunları öğrendik:
✔ Bağımsız olaylarda olasılığın nasıl çarpılarak hesaplandığını gördük.
✔ Bağımlı olaylarda ilk olayın ikinci olayı nasıl etkilediğini hesapladık.
✔ VEYA olaylarında iki olasılığı toplarken ortak durumları çıkardık.
✔ Gerçek hayatta birleşik olayların nasıl hesaplandığını öğrendik.