Matematikte bazı ifadeler sadece sayılardan oluşurken, bazı ifadeler harf ve sayıları bir arada içerir. İşte harfler ve sayılarla yazılan matematiksel ifadelere “Cebirsel İfadeler” denir.

Harfler, değişken (bilinmeyen) değerleri temsil eder. Sayılar ise katsayı olarak adlandırılır. Cebirsel ifadeler, eşitlik veya eşitsizlik içermeden matematiksel bir ifadeyi temsil eder.

✅ Örnekler:

• 3x + 5 → (x bilinmeyeni içerir)
• 2a – 7 → (a değişkeni vardır)
• y² + 4y – 9 → (y’nin karesi alınmıştır)

📌 Cebirsel ifadeler, günlük hayatta birçok alanda kullanılır:

• Alışverişte fiyat hesaplamaları,
• Geometri ve mühendislik problemleri,
• Fizik ve kimya formülleri.

Cebirsel İfadeler Konu Anlatımı (Terim, Katsayı, Değişken Kavramları)

Cebirsel ifadeler, harfler (değişkenler) ve sayıları (katsayılar) içeren matematiksel ifadeler olarak tanımlanır. Cebirsel ifadeleri anlamak için terim, değişken ve katsayı kavramlarını detaylıca inceleyelim.

1. Cebirsel İfadenin Bileşenleri

Bir cebirsel ifade terimlerden oluşur ve her terimde değişken, katsayı ve sabit terimler bulunabilir.

📌 Örnek Cebirsel İfade:

Burada:
✔ Değişken (x): Bilinmeyeni temsil eder.
✔ Katsayı (3 ve 5): Değişkenin önündeki sayıdır.
✔ Sabit terim (-7): Değişken içermeyen sayıdır.

✅ Örnekler:

📌 Not: Bir cebirsel ifadede sabit terim, değişken içermeyen terimdir.

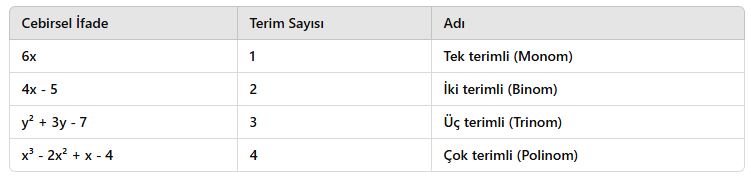
2. Tek Terimli ve Çok Terimli İfadeler

Cebirsel ifadeler içerdikleri terim sayısına göre sınıflandırılır.

📌 Tek Terimli İfade (Monom)
✔ Sadece bir terim içerir.
✔ Örnekler: 5x, -3y², 2a³

📌 İki Terimli İfade (Binom)
✔ İki terim içerir.
✔ Örnekler: 4x + 5, 3y² – 2y

📌 Üç Terimli İfade (Trinom)
✔ Üç terim içerir.
✔ Örnekler: x² + 2x + 1, 5a³ – 3a + 7

📌 Çok Terimli İfade (Polinom)
✔ Üçten fazla terim içerir.
✔ Örnekler: 2x³ – 4x² + x – 5

✅ Örnekler ve Terim Sayıları:

3. Cebirsel İfadelerde Terim Derecesi

📌 Terimin Derecesi:
✔ Bir terimin derecesi, değişkenin üstüyle belirlenir.
✔ Eğer birden fazla değişken varsa, tüm değişkenlerin üstlerinin toplamı alınır.

✅ Örnekler:

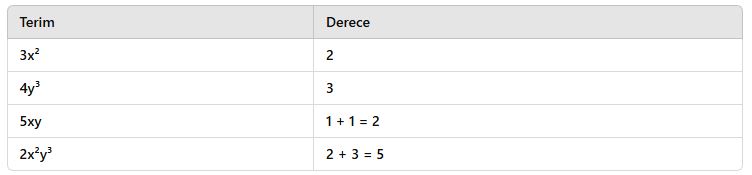
📌 Not:

• Sabit terimler (örneğin 7 veya -3), değişken içermediği için derecesi 0’dır.
• Tek bir değişken varsa, üstü o terimin derecesidir.

4. Gerçek Hayatta Cebirsel İfadeler Nerede Kullanılır?

📌 Örnek Kullanım Alanları:

✔ Alışverişte Fiyat Hesaplamaları:

• Bir markette x kg elma, y kg armut alındığında, toplam fiyat:

✔ Mühendislik ve Fizikte:

• Hız hesaplamaları:

✔ Bankacılık ve Faiz Hesaplamaları:

• Basit faiz formülü:

✅ Örnek:
Bir telefon hattının aylık ücreti 30 TL + her dakikaya 0,5 TL ücret ile hesaplanıyor.
Bir kişinin konuştuğu dakika x ise aylık faturası:

5. Cebirsel İfadelerde Örnek Sorular

📌 Soru 1: Aşağıdaki cebirsel ifadelerin terimlerini, değişkenlerini ve katsayılarını belirleyin.

a) 4x² – 3x + 7
b) 2y³ – 5y + 9

✔ Çözüm:

✅ Cevap: Tabloya göre belirlenmiştir.

📌 Soru 2:
Aşağıdaki terimlerin derecelerini bulun.

a) 6x³
b) 2xy²
c) 5x²y³
d) 4

✔ Çözüm:

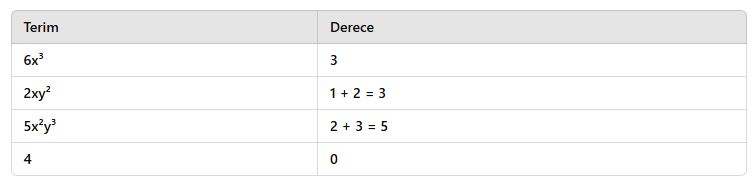
✅ Cevap: Tablodaki değerlerdir.

📌 Bu konuda öğrendiklerimiz:
✅ Cebirsel ifadelerin terim, değişken, katsayı ve sabit terim bileşenlerini öğrendik.
✅ Tek, iki, üç ve çok terimli ifadeleri tanımladık.
✅ Terim derecelerini hesapladık.
✅ Gerçek hayatta cebirsel ifadelerin nasıl kullanıldığını gördük.

Cebirsel İfadelerde İşlemler (Toplama, Çıkarma, Çarpma, Bölme)

Cebirsel ifadeler üzerinde toplama, çıkarma, çarpma ve bölme işlemleri yapılabilir. Bu işlemler benzer terimler kullanılarak gerçekleştirilir ve bazı kurallar takip edilir.

1. Cebirsel İfadelerde Toplama ve Çıkarma

📌 Temel Kural:
✔ Benzer terimler toplanır veya çıkarılır.
✔ Benzer terimler, değişkenleri ve üstleri aynı olan terimlerdir.

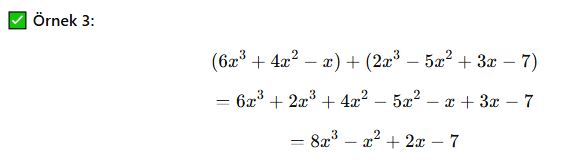
📌 Sonuç: Toplama ve çıkarma işlemlerinde benzer terimler birleştirilir.

2. Cebirsel İfadelerde Çarpma

Cebirsel ifadeleri çarparken çarpma kurallarına dikkat edilmelidir:

a) Tek Terim ile Çarpma

✔ Katsayılar çarpılır.
✔ Değişkenler çarpılırken üsleri toplanır.

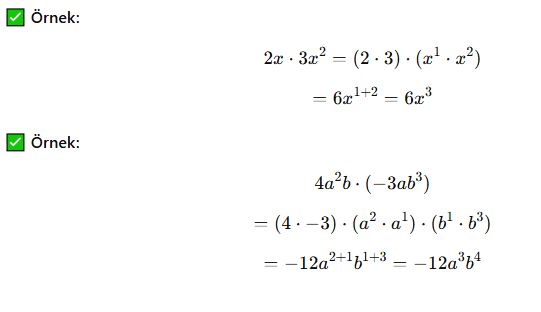
b) Dağılma Özelliği (Parantez Açma)

✔ Bir terimi parantez içindeki her terimle çarparız.

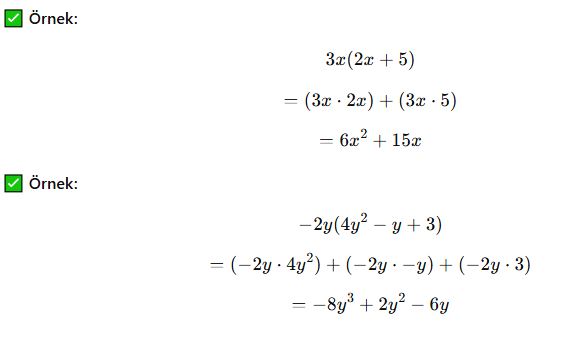
c) İki Parantezli İfadelerin Çarpımı

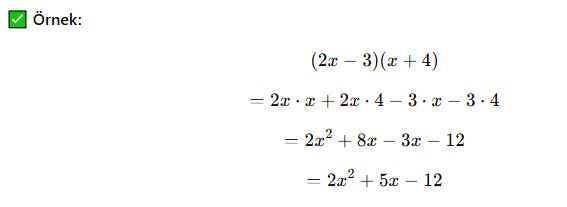
📌 Sonuç: İki parantezli ifadeler çarpılırken dağılma özelliği uygulanır.

3. Cebirsel İfadelerde Bölme

a) Tek Terim ile Bölme

✔ Katsayılar bölünür.
✔ Değişkenler bölünürken üsler çıkarılır.

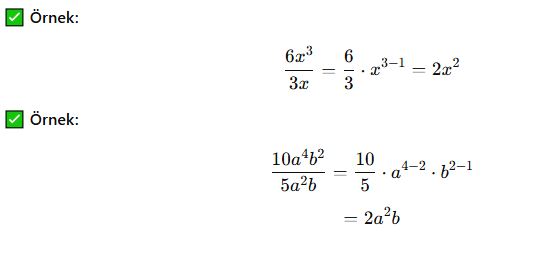
b) Çok Terimli İfadeyi Tek Terime Bölme

✔ Her terim tek tek bölünür.

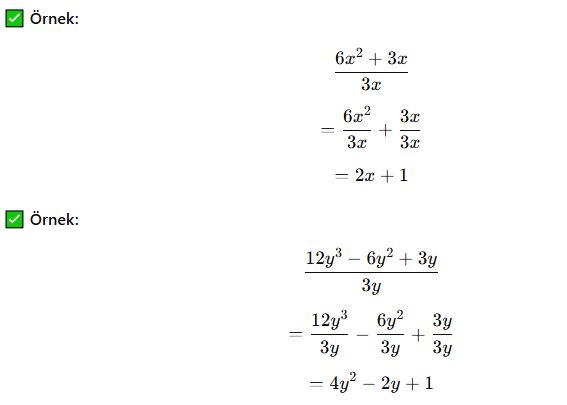
📌 Sonuç: Her terim ayrı ayrı bölünerek işlem yapılır.

4. Gerçek Hayatta Cebirsel İfadeler ile İşlemler

✔ Market hesaplamalarında indirim oranları hesaplanırken
✔ Fizikte hız-zaman formülleri kullanılırken
✔ Mühendislikte alan, hacim ve maliyet hesaplamalarında

✅ Örnek:
Bir kutu fiyatı 5x + 10 TL, bir müşteri x kutu alırsa toplam ödeme:

📌 Bu konuda öğrendiklerimiz:
✅ Benzer terimlerle toplama ve çıkarma işlemlerini öğrendik.
✅ Çarpma işleminde dağılma özelliğini ve iki parantezli ifadelerin çarpımını inceledik.
✅ Bölme işlemlerinde üsleri çıkararak hesaplama yaptık.
✅ Gerçek hayatta cebirsel ifadelerle işlemlerin nasıl kullanıldığını gördük.

Özdeşlikler ve Denklem Çözme

Matematikte bazı ifadeler her zaman doğru sonuç verirken, bazıları yalnızca belirli koşullarda doğrudur. Özdeşlikler, her zaman doğru olan cebirsel ifadelerken, denklemler yalnızca belirli değerler için sağlanan ifadelerdir.

1. Özdeşlik Nedir?

📌 Tanım:
Özdeşlik, değişken hangi değeri alırsa alsın her zaman doğru olan cebirsel ifadelerdir.

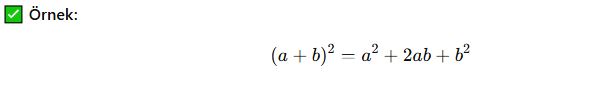
Bu özdeşlik her zaman doğrudur, çünkü dağılım özelliği ile kanıtlanabilir.

✔ Özdeşliklerde iki taraf her zaman eşittir.

📌 Sonuç: Özdeşlikler her zaman doğru olan ifadelerdir ve çarpanlara ayırma, denklem çözme gibi işlemlerde kullanılır.

2. Denklem Nedir?

📌 Tanım:
Denklem, bir değişkenin belirli bir değer için sağladığı eşitliktir.

Bu denklem yalnızca x = 2 için doğrudur.

📌 Denklemler değişkenin belli bir değeri için doğrudur, özdeşlikler ise her zaman doğrudur.

3. Denklem Çözme Yöntemleri

Bir denklem çözülürken değişken yalnız bırakılır ve değer bulunur.

✔ Temel Denklem Çözme Kuralları:
1️⃣ Eşitliğin her iki tarafına aynı sayı eklenebilir veya çıkarılabilir.
2️⃣ Her iki taraf aynı sayı ile çarpılabilir veya bölünebilir.
3️⃣ Denklem düzenlenerek değişken yalnız bırakılır.

📌 Sonuç: Denklemler, değişken yalnız bırakılarak çözülür.

4. Denklem Çözmede Özdeşlik Kullanımı

Bazı denklemleri çözerken özdeşliklerden faydalanabiliriz.

📌 Sonuç: Özdeşlikler, denklemleri çözerken büyük kolaylık sağlar.

5. Gerçek Hayatta Denklem Kullanımı

✔ Fizikte Hareket Denklemleri:

• Yol = Hız × Zaman → s = v × t

✔ Finans ve Bankacılıkta:

• Faiz = Anapara × Faiz Oranı × Süre

✔ İnşaat ve Mühendislikte:

• Alan = Uzunluk × Genişlik

✅ Örnek:
Bir araba x saat boyunca 60 km/h hızla giderse toplam aldığı yol:

📌 Sonuç: Deneylerde, mühendislik hesaplamalarında ve günlük hayatta denklemler sıklıkla kullanılır.

📌 Bu konuda öğrendiklerimiz:
✅ Özdeşliklerin her zaman doğru olan cebirsel ifadeler olduğunu öğrendik.
✅ Denklemlerin sadece belirli değişken değerleri için doğru olduğunu gördük.
✅ Denklem çözme kurallarını öğrendik ve pratik yaptık.
✅ Gerçek hayatta denklemlerin nasıl kullanıldığını inceledik.

Çarpanlara Ayırma ve Özdeşlikler

Matematikte bazı ifadeler daha küçük çarpanlara ayrılabilir. Bu yöntem, özellikle denklemleri çözerken ve özdeşlikleri kullanırken büyük kolaylık sağlar. Çarpanlara ayırma, cebirsel ifadeleri çarpım şeklinde yazma işlemidir.

1. Çarpanlara Ayırma Nedir?

📌 Tanım:
Çarpanlara ayırma, bir cebirsel ifadeyi iki veya daha fazla çarpanın çarpımı şeklinde yazma işlemidir.

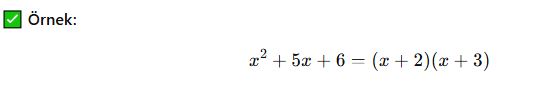
Burada çarpanlarına ayırarak ifadeyi iki parantezli biçimde yazdık.

✔ Çarpanlara ayırma, özellikle denklemleri çözerken çok önemlidir.

2. Ortak Çarpan Parantezine Alma

📌 Tanım:
Eğer bir cebirsel ifadede bütün terimlerde ortak bir çarpan varsa, bu çarpan parantez dışına alınabilir.

Burada 4ab ortak çarpan olduğu için dışarı aldık.

📌 Sonuç: Ortak çarpan parantezine almak, ifadeyi çarpım şeklinde yazmanın ilk adımıdır.

3. İki Kare Farkı Özdeşliği

📌 Özdeşlik:

📌 Sonuç: İki kare farkı, çarpanlara ayırmayı hızlandıran özel bir özdeşliktir.

4. Tam Kare Özdeşlikleri ile Çarpanlara Ayırma

✔ İki terim toplamının karesi:

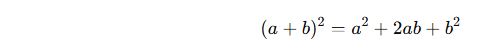
✔ İki terim farkının karesi:

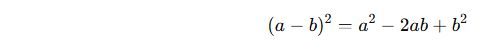
📌 Sonuç: Tam kare ifadeleri tanımak, çarpanlara ayırmayı kolaylaştırır.

5. Çarpanlarına Ayırma Yöntemi: Çarpımları ve Toplamları Verilen Sayılar

📌 Yöntem:
x² + bx + c şeklindeki ifadeyi çarpanlarına ayırırken, çarpımları c, toplamları b olan iki sayı bulunur.

📌 Sonuç: Çarpanlara ayırmada sayıları dikkatli seçmek gerekir.

6. Çarpanlara Ayırma ile Denklem Çözme

Bazı denklemler, çarpanlara ayrılarak kolayca çözülebilir.

📌 Sonuç: Çarpanlara ayırma, denklemleri hızlıca çözmeyi sağlar.

7. Gerçek Hayatta Çarpanlara Ayırma ve Özdeşlikler

✔ Mühendislikte: Alan ve hacim hesaplamalarında kullanılır.
✔ Fizikte: Hareket ve enerji formüllerinde özdeşlikler kullanılır.
✔ İstatistikte: Veri analizlerinde matematiksel modelleme yapılır.

✅ Örnek:
Bir dikdörtgenin alanı x² + 7x + 10 olarak verilmişse,
bu alan (x + 5)(x + 2) şeklinde yazılabilir.

📌 Sonuç: Çarpanlara ayırma, mühendislikten ekonomiye birçok alanda kullanılır.

📌 Bu konuda öğrendiklerimiz:
✅ Çarpanlara ayırmanın temel yöntemlerini öğrendik.
✅ Ortak çarpan parantezine alma tekniğini inceledik.
✅ İki kare farkı özdeşliği ile çarpanlara ayırma yaptık.
✅ Tam kare ifadeleri nasıl çarpanlarına ayıracağımızı öğrendik.
✅ Denklem çözümünde çarpanlara ayırmanın önemini gördük.

Gerçek Hayatta Cebirsel İfadeler ve Kullanımı

Cebirsel ifadeler, sadece matematik derslerinde değil, günlük hayatın birçok alanında da karşımıza çıkar. Alışverişten mühendisliğe, ekonomiden fiziğe kadar birçok alanda cebirsel ifadeler kullanılır.

1. Alışverişte Cebirsel İfadeler

Günlük hayatta alışveriş yaparken fiyat hesaplamalarında cebirsel ifadeler kullanılır.

✅ Örnek:
Bir manavda x kg elma ve y kg armut alındığında toplam ödeme şu şekilde hesaplanabilir:

Toplam Fiyat=10x+8y

Eğer bir müşteri 3 kg elma ve 2 kg armut alırsa:

📌 Sonuç: Fiyat hesaplamalarında cebirsel ifadeler büyük kolaylık sağlar.

2. Ulaşım ve Yol Problemlerinde Cebirsel İfadeler

Fizikte hız, yol ve zaman hesaplamaları cebirsel ifadelerle yapılır.

📌 Sonuç: Ulaşımda zaman ve hız hesaplamalarında cebirsel ifadeler kullanılır.

3. İnşaat ve Mühendislikte Cebirsel İfadeler

Mühendislik ve inşaat sektörlerinde alan, hacim, maliyet hesaplamaları cebirsel ifadelerle yapılır.

📌 Örnek – Dikdörtgen Alanı:
Bir odanın uzunluğu x metre, genişliği y metre ise alan:

✅ Örnek:
Bir odanın uzunluğu 5 metre, genişliği 4 metre ise:

📌 Sonuç: İnşaat projelerinde cebirsel ifadeler kullanılarak maliyet ve alan hesaplamaları yapılır.

4. Finans ve Bankacılıkta Cebirsel İfadeler

✔ Faiz hesaplamalarında, yatırım getirisi analizlerinde cebirsel ifadeler kullanılır.

📌 Basit Faiz Formülü:

Faiz = Anapara × Faiz Oranı × Süre

✅ Örnek:
Bir bankaya x TL yatırıldığında %5 faizle 3 yıl sonra toplam kazanç:

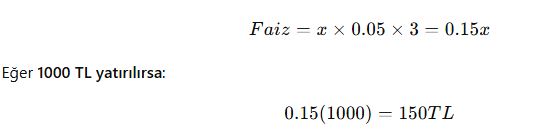
📌 Sonuç: Bankacılıkta faiz ve yatırım analizleri cebirsel ifadelerle hesaplanır.

5. Bilim ve Fizikte Cebirsel İfadeler

✔ Hareket denklemleri, enerji hesaplamaları, elektrik devreleri gibi alanlarda cebir kullanılır.

📌 Örnek – Hareket Formülü:
Bir cismin hareket denklemi:

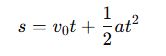
📌 Örnek – Elektrik Akımı:
Bir devredeki direnç şu formülle hesaplanır:

(V: Gerilim, I: Akım, R: Direnç)

📌 Sonuç: Fizik ve mühendislik alanlarında cebirsel ifadelerle hesaplamalar yapılır.

6. Günlük Hayatta Cebir Kullanımı

✔ Market indirimleri: Cebirsel ifadelerle fiyat değişimleri hesaplanır.
✔ Vergi hesaplamaları: Gelir ve gider analizleri yapılır.
✔ Spor analizleri: Maç istatistikleri ve oyuncu performansları hesaplanır.

✅ Örnek:
Bir mağazada x TL’lik bir ürüne %20 indirim yapılırsa:

📌 Sonuç: Günlük hayatta indirimler ve bütçe planlamaları cebirle hesaplanır.

📌 Bu konuda öğrendiklerimiz:
✅ Alışverişte fiyat hesaplamaları için cebirsel ifadeler kullanılır.
✅ Ulaşımda hız, yol ve zaman hesaplamaları cebirle yapılır.
✅ Mühendislikte alan, hacim ve maliyet hesaplamaları cebir kullanılarak çözülür.
✅ Bankacılıkta faiz ve yatırım analizlerinde cebirsel formüller uygulanır.
✅ Fizik, elektrik ve spor analizlerinde cebir kullanımı yaygındır.

Cebirsel İfadeler ve Özdeşlikler Çözümlü Örnek Sorular

1. Cebirsel İfadelerde Toplama ve Çıkarma

2. Cebirsel İfadelerde Çarpma

3. İki Parantezli İfadelerin Çarpımı

4. Ortak Çarpan Parantezine Alma

5. Çarpanlara Ayırma – İki Kare Farkı

📌 Soru 5:
Aşağıdaki ifadeyi çarpanlarına ayırın:

Çözüm:
Bu ifade iki kare farkı özdeşliği ile açılabilir:

✅ Cevap: (x – 3)(x + 3)

6. Denklem Çözme – Temel Seviye

📌 Soru 6:
Aşağıdaki denklemi çözün:

7. Denklem Çözme – Orta Seviye

📌 Soru 7:
Aşağıdaki denklemi çözün:

8. Çarpanlara Ayırma – Çarpımları ve Toplamları Verilen Sayılar

📌 Soru 8:
Aşağıdaki ifadeyi çarpanlarına ayırın:

9. Cebirsel İfadelerde Bölme

📌 Soru 9:
Aşağıdaki ifadeyi sadeleştirin:

10. Gerçek Hayatta Cebir Kullanımı

📌 Soru 10:
Bir ürünün fiyatı x TL ve mağazada %20 indirim uygulanıyor.
İndirim sonrası fiyatı veren cebirsel ifadeyi yazın.

Çözüm:

• İndirim miktarı: 0.2x
• Yeni fiyat:

✅ Cevap: 0.8x

📌 Bu 10 soru ile şunları öğrendik:
✔ Cebirsel ifadelerde toplama, çıkarma ve çarpma işlemleri yaptık.
✔ Çarpanlara ayırma yöntemlerini kullandık.
✔ Denklem çözme tekniklerini uyguladık.
✔ Gerçek hayatta cebirsel ifadelerin nasıl kullanıldığını gördük.