8. Sınıf Matematik Doğrusal Denklemler Konu Anlatımı

Matematikte birçok olay iki değişken arasındaki ilişkiyi gösterir. Doğrusal denklemler, bu ilişkiyi bir doğru ile ifade eden birinci dereceden denklemlerdir. Örneğin, y = 2x + 3 gibi bir denklem, bir doğrunun matematiksel ifadesidir ve bir değişkenin diğerine nasıl bağlı olduğunu gösterir.

Bu konuda şunları öğreneceğiz:
📌 Birinci dereceden bir bilinmeyenli denklemleri çözme
📌 Koordinat sistemi ve sıralı ikilileri anlama
📌 Doğrusal denklemleri tablo ve grafiklerle ifade etme
📌 Gerçek hayatta doğrusal ilişkileri modelleme
📌 Doğrunun eğimini hesaplama ve yorumlama

Birinci Dereceden Bir Bilinmeyenli Denklemler

📌 Tanım:
Bir bilinmeyen içeren ve birinci dereceden (üsleri 1 olan) ifadeler içeren denklemler birinci dereceden bir bilinmeyenli denklemler olarak adlandırılır.

✅ Örnekler:

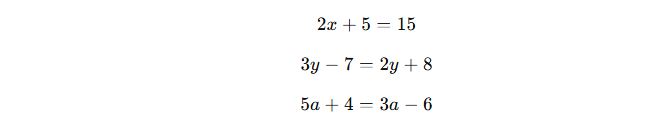
Bu denklemler x, y, a gibi bilinmeyenler içerir ve üssü 1 olduğu için “birinci dereceden” olarak adlandırılır.

Denklem Çözme Yöntemleri

Bir denklemi çözerken amaç, bilinmeyeni yalnız bırakmak ve sonucunu bulmaktır.

✔ Temel Kurallar:
1️⃣ Eşitliğin her iki tarafına aynı sayı eklenebilir veya çıkarılabilir.
2️⃣ Her iki taraf aynı sayı ile çarpılabilir veya bölünebilir.
3️⃣ Bilinmeyen bir taraf, sayılar diğer tarafa alınır.

✅ Örnek 1 – Basit Denklem Çözme

✅ Örnek 2 – Denklemde Bilinmeyen İki Tarafta

✅ Örnek 3 – Dağılma Özelliği Kullanma

📌 Sonuç: Birinci dereceden denklemler çözülürken bilinmeyen yalnız bırakılır.

Koordinat Sistemi ve Sıralı İkililer

Doğrusal denklemleri grafik üzerinde göstermek için önce koordinat sistemini ve sıralı ikilileri iyi anlamamız gerekir. Bu bölümde koordinat sisteminin yapısını öğrenecek ve sıralı ikilileri nasıl kullanacağımızı inceleyeceğiz. 🚀

1. Koordinat Sisteminin Tanımı

📌 Tanım:
Koordinat sistemi, iki sayı doğrusunun dik kesişmesiyle oluşan düzlemdir. Bu sistem iki boyutlu uzaydaki noktaları göstermek için kullanılır.

✔ Yatay eksen → x ekseni
✔ Dikey eksen → y ekseni
✔ Kesim noktası (0,0) → Orijin

📌 Örnek Koordinat Sistemi:

✔ Koordinat düzlemi, dört bölgeye ayrılır:
1️⃣ 1. Bölge (x > 0, y > 0)
2️⃣ 2. Bölge (x < 0, y > 0)
3️⃣ 3. Bölge (x < 0, y < 0)
4️⃣ 4. Bölge (x > 0, y < 0)

✅ Örnek:

• (3, 4) noktası → 1. Bölgede
• (-2, 5) noktası → 2. Bölgede
• (-4, -3) noktası → 3. Bölgede
• (6, -2) noktası → 4. Bölgede

📌 Sonuç: Koordinat sistemi, noktaları grafik üzerinde belirlemek için kullanılır.

2. Sıralı İkililer Nedir?

📌 Tanım:
Sıralı ikili, bir noktanın koordinatlarını gösteren (x, y) biçimindeki ifadedir.

✔ İlk sayı (x), yatay eksendeki konumu gösterir.
✔ İkinci sayı (y), dikey eksendeki konumu gösterir.

✅ Örnekler:

📌 Örnek Noktalar:

• (4, 5) → x = 4, y = 5 → 1. Bölgede
• (-3, 6) → x = -3, y = 6 → 2. Bölgede
• (-2, -4) → x = -2, y = -4 → 3. Bölgede
• (5, -7) → x = 5, y = -7 → 4. Bölgede

📌 Sonuç: Sıralı ikililer, noktaların koordinat düzleminde yerini belirlemek için kullanılır.

3. Koordinat Sisteminde Nokta Gösterme

Bir noktayı koordinat sisteminde göstermek için:
1️⃣ x ekseninde belirtilen kadar sağa veya sola gidilir.
2️⃣ y ekseninde yukarı veya aşağı gidilir.
3️⃣ Nokta belirtilen yerde işaretlenir.

✅ Örnek:
Aşağıdaki noktaları koordinat sisteminde gösterelim:

• A(3, 2) → x = 3 sağa, y = 2 yukarı
• B(-4, 5) → x = -4 sola, y = 5 yukarı
• C(0, -3) → x = 0, y = -3 aşağı (y ekseni üzerinde)
• D(6, 0) → x = 6 sağa, y = 0 (x ekseni üzerinde)

📌 Sonuç: Koordinat sisteminde noktalar sıralı ikililerle belirlenir.

4. Gerçek Hayatta Koordinat Sistemi Kullanımı

✔ Harita ve Navigasyon: Konum belirleme GPS sistemleri sıralı ikililere dayanır.
✔ Grafik Çizimleri: Veri analizlerinde doğruların gösterilmesinde kullanılır.
✔ Bilgisayar Oyunları: 2D ve 3D oyunlarda nesnelerin konumları sıralı ikililerle belirlenir.

✅ Örnek:
Bir telefon uygulamasında, kullanıcının bulunduğu konum (x, y) koordinatlarıyla belirlenir.

📌 Bu konuda öğrendiklerimiz:
✅ Koordinat sisteminin temel özelliklerini öğrendik.
✅ Sıralı ikililerin nasıl gösterildiğini inceledik.
✅ Noktaların koordinat düzleminde nasıl yerleştirileceğini öğrendik.
✅ Gerçek hayatta koordinat sisteminin nasıl kullanıldığını gördük.

Aralarında Doğrusal İlişki Bulunan İki Değişkeni Tablo ve Denklem ile İfade Etme

Matematikte birçok durumda iki değişken arasında doğrusal bir ilişki bulunur. Bu ilişki bir denklemle ifade edilebilir ve tablo ya da grafik ile gösterilebilir.

1. Doğrusal İlişki Nedir?

📌 Tanım:
Bir değişken arttığında diğer değişken de belirli bir kurala göre artıyor veya azalıyorsa, iki değişken arasında doğrusal bir ilişki vardır.

✔ Doğrusal ilişkiler genellikle şu şekilde ifade edilir:

Burada:

• y: Bağımlı değişken (çıktı)
• x: Bağımsız değişken (girdi)
• m: Doğrunun eğimi (x arttığında y’nin değişme miktarı)
• b: y eksenini kestiği nokta (sabit terim)

✅ Örnek:
Bir kafede çay 5 TL, kahve 10 TL ise, toplam ödeme şu şekilde ifade edilir:

Burada:

• x: Çay sayısı
• y: Kahve sayısı
• T: Toplam ödeme

2. Tablo ile Doğrusal İlişkiyi Gösterme

Doğrusal ilişkiyi göstermek için bir tablo oluşturabiliriz.

📌 Örnek:
Bir öğrenci saatte 3 km hızla yürüyorsa, toplam yol (y) ile zaman (x) arasındaki ilişki şu şekildedir:

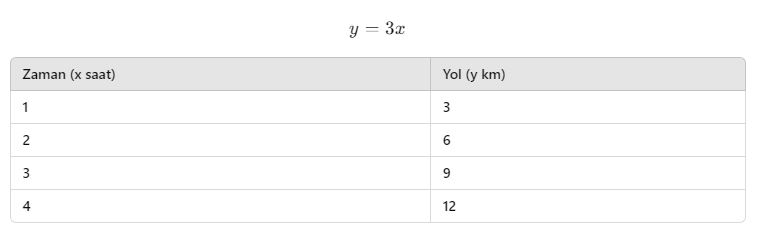
Bu tablo doğrusal bir ilişkiyi gösterir. Çünkü:
✔ Her saat için yol sabit bir şekilde artar.
✔ Denklem y = 3x ile tanımlanabilir.

📌 Sonuç: Tablolar, doğrusal ilişkileri anlamak için kullanılır.

3. Doğrusal Denklemi Kullanarak Tablo Oluşturma

Bir denklem verildiğinde, x değerlerini seçerek y değerlerini hesaplayarak tablo oluşturabiliriz.

✅ Örnek:
Denklem:

📌 Sonuç: Denklemden elde edilen tablo, değişkenler arasındaki ilişkiyi gösterir.

4. Gerçek Hayatta Doğrusal İlişkiler

Bu doğrusal ilişkiyi tablo ve grafikle gösterebiliriz.

📌 Sonuç: Günlük hayatta birçok olay doğrusal ilişkilerle ifade edilir.

📌 Bu konuda öğrendiklerimiz:
✅ Doğrusal ilişkinin ne olduğunu öğrendik.
✅ Doğrusal denklemi kullanarak tablo oluşturduk.
✅ Gerçek hayatta doğrusal ilişkilerin nasıl kullanıldığını gördük.

Doğrusal Denklemlerin Grafiğini Çizme

Bir doğrusal denklemin grafiğini çizmek, x ve y değişkenleri arasındaki ilişkiyi görselleştirmek için önemlidir. Birinci dereceden iki bilinmeyenli denklemler bir doğruyu temsil eder ve bu doğruyu koordinat sisteminde göstermek için bazı yöntemler kullanılır.

1. Doğrusal Denklemin Grafiğini Çizme Adımları

Bir doğrusal denklemin grafiğini çizmek için şu adımları izleriz:

1️⃣ Denklemi belirleyin.
2️⃣ Bazı x değerleri için y’yi hesaplayarak bir tablo oluşturun.
3️⃣ Tablodaki noktaları koordinat sistemine yerleştirin.
4️⃣ Noktaları birleştirerek doğruyu çizin.

✅ Örnek:
Verilen denklem:

📌 Sonuç: Bu noktalar (-2,-3), (-1,-1), (0,1), (1,3), (2,5) koordinat düzlemine işaretlenir ve noktalar birleştirilerek doğru elde edilir.

2. Doğrusal Denklemin Grafik Üzerindeki Özellikleri

✔ Denklem y = mx + b formundaysa:

• m → eğimdir (doğrunun dikliği veya yataylığı)
• b → y eksenini kestiği noktadır

📌 Örnek 1:
Denklem:

• Eğim (m) = 3 (Her 1 birim sağa gidildiğinde, 3 birim yukarı çıkılır.)
• y ekseni kesişim noktası (b) = -2 (Doğru y eksenini -2 noktasında keser.)

✔ Grafikte bu bilgilerle doğrunun eğimini ve başlangıç noktasını belirleyebiliriz.

3. x ve y Ekseni Kesişme Noktaları ile Grafik Çizme

Bir doğrunun x ve y ekseniyle kesiştiği noktalar bulunarak da grafik çizilebilir.

✅ Bu iki nokta koordinat sistemine yerleştirilerek doğru çizilir.

4. Gerçek Hayatta Doğrusal Grafikler

✔ Hız-Zaman Grafiklerinde:

• Bir araç sabit hızla ilerliyorsa, doğrusal grafik oluşur.

✔ Elektrik Faturası Hesaplamalarında:

• Sabit ücret + kullanılan enerji doğrusal bir ilişki oluşturur.

✔ Para-Birikim Planlarında:

• Aylık düzenli birikim yapan kişinin toplam parası doğrusal artış gösterir.

✅ Örnek:
Bir kişi her ay 500 TL biriktirirse, toplam para şu denklemle ifade edilir:

y=500x

Bu denklemin grafiği her ay sabit artışı gösteren bir doğru oluşturur.

📌 Bu konuda öğrendiklerimiz:
✅ Bir doğrusal denklemin grafiğinin nasıl çizileceğini öğrendik.
✅ x ve y ekseni kesişim noktalarıyla grafik çizdik.
✅ Gerçek hayatta doğrusal grafiklerin nasıl kullanıldığını gördük.

Doğrusal İlişki İçeren Gerçek Hayat Durumlarını Denklem, Tablo ve Grafik ile Yorumlama

Matematikte doğrusal denklemler yalnızca soyut matematik işlemleri için değil, günlük hayatta karşılaştığımız birçok durumu modellemek için de kullanılır. Gelir-gider hesaplamaları, hız-zaman ilişkisi, fatura hesaplamaları, inşaat projeleri ve üretim planlamaları gibi birçok alanda doğrusal denklemler, tablolar ve grafikler yardımıyla analiz yapılır.

1. Gerçek Hayatta Doğrusal Denklem Kullanımı

📌 Tanım:
Bir olay veya durum belirli bir kurala göre düzenli bir artış veya azalış gösteriyorsa, bunu bir doğrusal denklemle ifade edebiliriz.

✔ Genel denklem formu:

Burada:

• y: Bağımlı değişken (çıktı)
• x: Bağımsız değişken (girdi)
• m: Eğim (x değiştikçe y’nin nasıl değiştiğini gösterir)
• b: Başlangıç değeri (y eksenini kestiği nokta)

2. Gerçek Hayattan Örnekler

Örnek 1: Birikim Hesaplama

Bir öğrenci her hafta 50 TL biriktiriyor.
Başlangıçta elinde 100 TL var.
Her hafta toplam para şu şekilde hesaplanır:

y=50x+100

✔ Burada:

• x: Hafta sayısı
• y: Toplam birikim
• m = 50: Her hafta eklenen miktar
• b = 100: Başlangıç parası

📌 Tablo:

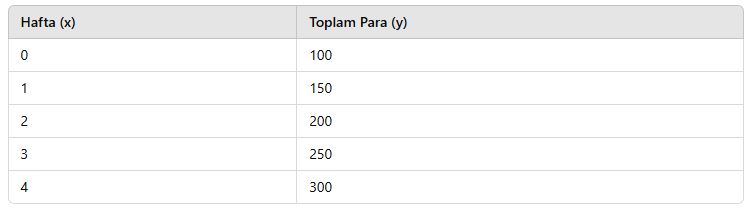
📌 Grafik:
Bu noktalar koordinat sistemine yerleştirildiğinde doğrusal bir doğru oluşur.

Örnek 2: Hız-Zaman İlişkisi

Bir araç saatte 80 km hızla hareket ederse, geçen saatlere bağlı olarak alınan yol şu şekilde hesaplanır:

y=80x

✔ Burada:

• x: Geçen saat
• y: Alınan yol (km)
• m = 80: Araç her saat 80 km yol alıyor
• b = 0: Başlangıç noktası (0 km)

📌 Tablo:

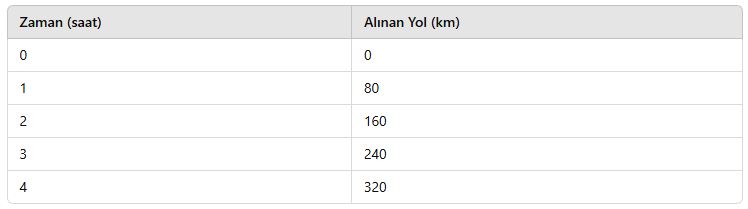
📌 Grafik:
Grafik çizildiğinde orijinden geçen doğrusal bir çizgi elde edilir.

Örnek 3: Elektrik Faturası Hesaplama

Bir evde sabit 30 TL’lik dağıtım bedeli ve kullanılan her kWh başına 2 TL ücret vardır.
Toplam fatura şu şekilde hesaplanır:

T=30+2x

✔ Burada:

• x: Kullanılan kWh
• T: Toplam fatura tutarı
• m = 2: Her kWh başına eklenen ücret
• b = 30: Sabit ücret

📌 Tablo:

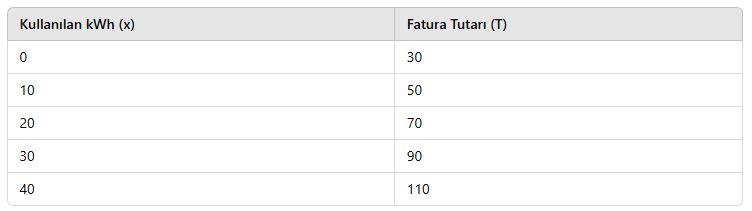
📌 Grafik:
Grafikte y eksenini 30 noktasında kesen bir doğru oluşur.

3. Doğrusal Denklem, Tablo ve Grafik ile Yorumlama

✔ Doğrusal denklem, iki değişken arasındaki düzenli artış veya azalışı gösterir.
✔ Tablo, belirli x değerleri için y’nin nasıl değiştiğini gösterir.
✔ Grafik, değişkenler arasındaki ilişkiyi görsel olarak anlamamıza yardımcı olur.

✅ Özet:

• y = mx + b formülü kullanılarak gerçek hayat problemleri modellenebilir.
• Tablo oluşturarak belirli x değerlerine karşılık gelen y değerleri hesaplanır.
• Noktalar koordinat sistemine yerleştirilerek doğru çizilir ve yorumlanır.

Doğrunun Eğimini Modellerle Açıklama ve Doğrusal Denklemleri Eğimle İlişkilendirme

Doğrusal denklemlerle çalışırken eğim (m) kavramı büyük önem taşır. Eğim, doğrunun ne kadar dik ya da yatay olduğunu gösterir ve x değiştikçe y’nin nasıl değiştiğini ifade eder.

1. Doğrunun Eğimini Modellerle Açıklama

📌 Tanım:
Eğim, bir doğrunun yatay eksene göre ne kadar dik olduğunu gösterir.
Matematikte eğim (m) şu formülle hesaplanır:

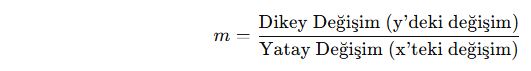
Eğim, iki nokta arasındaki y değerinin farkının x değerinin farkına bölünmesiyle bulunur.

✅ Örnek:
A(2, 3) ve B(5, 9) noktaları arasındaki doğrunun eğimini bulalım.

✔ Formülü kullanarak:

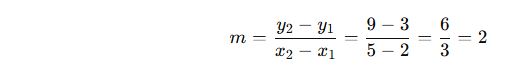
📌 Sonuç: Eğim 2 olduğuna göre, x 1 arttığında y 2 artar.

2. Eğim Türleri ve Yorumu

✔ Pozitif Eğim (m > 0):

• Doğru yukarı eğimli olur.
• x arttıkça y de artar.
• Örnek: y = 2x + 3

✔ Negatif Eğim (m < 0):

• Doğru aşağı eğimli olur.
• x arttıkça y azalır.
• Örnek: y = -3x + 5

✔ Eğim Sıfır (m = 0):

• Doğru yataydır (sabit fonksiyon).
• Örnek: y = 4

✔ Tanımsız Eğim:

• Doğru dikeyse, eğim tanımsızdır.
• Örnek: x = 3

📌 Özet:

• m > 0 → Doğru yukarı eğimli
• m < 0 → Doğru aşağı eğimli
• m = 0 → Yatay doğru
• Tanımsız eğim → Dikey doğru

3. Doğrusal Denklemleri Eğimle İlişkilendirme

Bir doğrusal denklem y = mx + b formunda yazılabilir:

✔ m: Eğim (x arttığında y’nin değişme miktarı)
✔ b: y ekseni kesişim noktası

4. Gerçek Hayatta Eğim Kullanımı

✔ Yol eğimleri: Yolun dikliği eğim ile hesaplanır.
✔ Merdiven ve rampa tasarımı: Eğim hesaplanarak yapılır.
✔ Borsa analizleri: Artış ve azalışlar doğrusal grafiklerle analiz edilir.

📌 Örnek:
Bir asansör her 2 saniyede 3 metre yükseliyorsa, eğim:

📌 Bu konuda öğrendiklerimiz:
✅ Eğim kavramını ve hesaplanmasını öğrendik.
✅ Eğim türlerini ve nasıl yorumlanacağını inceledik.
✅ Doğrusal denklemleri eğim ile ilişkilendirdik.
✅ Gerçek hayatta eğimin nasıl kullanıldığını öğrendik.

8. Sınıf Matematik Doğrusal Denklemler Çözümlü Örnek Sorular

1. Doğrusal Denklem Çözme

📌 Soru 1:
Aşağıdaki doğrusal denklemi çözerek x değerini bulun:

2. İki Nokta Arasındaki Eğim

📌 Soru 2:
A(1, 4) ve B(3, 10) noktaları arasındaki eğimi hesaplayın.

Çözüm:

3. Doğrusal Denklemin Eğimini Bulma

📌 Soru 3:
Aşağıdaki denklemde eğimi bulun:

Çözüm:
✔ Denklem y = mx + b formundadır.
✔ Eğim (m) = -5

✅ Cevap: Eğim = -5

4. Doğrunun x ve y Ekseni Kesişme Noktaları

📌 Soru 4:
Aşağıdaki doğrunun x ve y ekseni kesişim noktalarını bulun:

5. Doğrusal Denkleme Uygun Tablo Oluşturma

📌 Soru 5:
Aşağıdaki denklem için x ve y değerlerini içeren bir tablo oluşturun:

6. Doğrusal Denklemin Grafiğini Çizme

📌 Soru 6:
Aşağıdaki doğrusal denklemin grafiğini çizin:

✔ Grafik çizerken noktalar (-2,6), (-1,5), (0,4), (1,3), (2,2) işaretlenir ve birleştirilir.

✅ Cevap: Grafik y eksenini 4’te kesen ve negatif eğimli bir doğrudur.

7. Gerçek Hayatta Eğim Kullanımı

📌 Soru 7:
Bir asansör her 3 saniyede 2 metre yükseliyorsa, asansörün hareketini gösteren doğrusal denklem nedir?

Çözüm:
✔ Eğim (m):

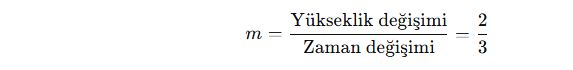
✔ Başlangıç noktası (b = 0, başlangıçta yere yakın):

✔ Denklem:

✅ Cevap: y = (2/3)x

8. Eğim Kullanarak Doğru Denklemi Yazma

📌 Soru 8:
Bir doğru, (-1,2) noktasından geçiyor ve eğimi m = 4.
Bu doğrunun denklemini yazın.

Çözüm:

9. Eğim Sıfır ve Tanımsız Olan Doğrular

📌 Soru 9:
Aşağıdaki doğruların eğimlerini belirleyin:

a) y = 5
b) x = -3

Çözüm:
✔ a) y = 5 → Yatay doğru → Eğimi 0’dır.
✔ b) x = -3 → Dikey doğru → Eğim tanımsızdır.

✅ Cevap:
a) Eğim = 0
b) Eğim tanımsızdır.

10. x ve y Ekseni Kesişimi Olan Bir Doğrunun Denklemini Yazma

📌 Soru 10:
Bir doğru x eksenini (6,0) noktasında, y eksenini (0,-3) noktasında kesiyor.
Bu doğrunun denklemini yazın.

Çözüm:

📌 Bu 10 soru ile şunları öğrendik:
✔ Doğrusal denklemler çözdük.
✔ İki nokta arasındaki eğimi hesapladık.
✔ Denklemi verilen doğruların grafiklerini çizdik.
✔ Gerçek hayatta eğim ve doğrusal denklemlerin nasıl kullanıldığını gördük.
✔ x ve y ekseni kesişimleri ile doğru denklemi yazdık.

Doğrusal Denklemler Konu Özeti

Bu konu boyunca doğrusal denklemleri, eğim kavramını, grafik çizmeyi ve gerçek hayattaki kullanım alanlarını öğrendik. İşte öğrendiklerimizin kısa bir özeti:

1. Doğrusal Denklem Nedir?

📌 Birinci dereceden iki bilinmeyenli denklemler, doğrusal denklemler olarak adlandırılır.
✔ Genel formu:

✔ m: Doğrunun eğimi
✔ b: Doğrunun y eksenini kestiği nokta

✅ Örnekler:

• y = 2x + 3 (Pozitif eğimli doğru)
• y = -x + 5 (Negatif eğimli doğru)
• y = 4 (Yatay doğru, eğimi 0)
• x = -2 (Dikey doğru, eğim tanımsız)

2. Doğrunun Eğimini Hesaplama

3. Doğrusal Denklemlerin Grafiğini Çizme

✔ Bir doğrunun grafiğini çizmek için:
1️⃣ Denklem belirlenir.
2️⃣ x değerleri verilerek y hesaplanır ve bir tablo oluşturulur.
3️⃣ Koordinat sistemi üzerinde noktalar yerleştirilir.
4️⃣ Noktalar birleştirilerek doğru çizilir.

✅ Örnek:
Denklem:

📌 Grafik çizildiğinde doğru y eksenini 1 noktasında keser ve eğimi 2 olduğu için yukarıya doğru eğimlidir.

4. Doğrunun x ve y Ekseni Kesişimi

✔ x ekseni kesişim noktası (y = 0 için x bulunur).
✔ y ekseni kesişim noktası (x = 0 için y bulunur).

✅ Örnek:
Denklem:

• x eksenini kestiği nokta: (2,0)
• y eksenini kestiği nokta: (0,3)

5. Gerçek Hayatta Doğrusal Denklemler

📌 Bu konu kapsamında öğrendiklerimiz:
✅ Doğrusal denklemin temel yapısını öğrendik.
✅ Eğim kavramını ve nasıl hesaplanacağını inceledik.
✅ x ve y ekseni kesişim noktalarını bulduk.
✅ Gerçek hayatta doğrusal denklemleri nasıl kullanabileceğimizi gördük.