8. Sınıf Matematik Eşlik ve Benzerlik Konu Anlatımı

Geometri, şekiller arasındaki ilişkileri inceleyen bir matematik dalıdır. Bu bağlamda eşlik ve benzerlik, iki şeklin birbirine ne kadar benzediğini veya birebir aynı olup olmadığını anlamamızı sağlar.

✔ Eşlik, iki şeklin birebir aynı olmasıdır.
✔ Benzerlik, iki şeklin aynı oranda büyütülmüş veya küçültülmüş hali olmasıdır.

Bu konu kapsamında eş ve benzer şekillerin özelliklerini ve benzerlik oranlarını detaylı bir şekilde inceleyeceğiz. 🚀

Eşlik Nedir?

📌 Tanım:
İki şekil eş ise, birebir aynı boyutta ve aynı şekilde olmalıdır. Eş şekillerin tüm kenar uzunlukları ve açı ölçüleri birbirine eşittir.

✔ Eşlik, şeklin döndürülmesi, kaydırılması veya yansıması ile değişmez.
✔ Eş şekillerin uzunlukları ve açıları birebir aynıdır.
✔ Eşlik “≅” sembolü ile gösterilir.

🚀 Özetle, iki şekil eş ise, tamamen aynı şekil ve boyuttadırlar.

1. Eş Üçgenlerin Özellikleri

📌 İki üçgenin eş olabilmesi için aşağıdaki şartlar sağlanmalıdır:

✔ SSS (Sıra Sıra Üç Kenar Eşitliği):

• Üç kenarı da birbirine eşit olan üçgenler eş üçgendir.

✔ KSK (Kenar – Açı – Kenar):

• İki kenarı ve aralarındaki açı eşit olan üçgenler eş üçgendir.

✔ ASA (Açı – Kenar – Açı):

• İki açısı ve arasındaki kenarı eşit olan üçgenler eş üçgendir.

✔ 90°DK (Dik Kenar – Hipotenüs Eşliği):

• Dik üçgenlerde hipotenüs ve bir dik kenar eşitse, üçgenler eş üçgendir.

✅ Örnek:
Aşağıdaki üçgenlerin kenar uzunlukları verilmiştir:

• ABC üçgeni: AB = 5 cm, BC = 7 cm, AC = 6 cm
• DEF üçgeni: DE = 5 cm, EF = 7 cm, DF = 6 cm

Bu üçgenler SSS kuralına göre eş üçgendir.

✔ Gösterim:

📌 Sonuç: Eş üçgenlerin kenar uzunlukları ve açı ölçüleri birebir aynıdır.

2. Eş Dörtgenlerin Özellikleri

📌 İki dörtgenin eş olması için:
✔ Tüm kenar uzunlukları eşit olmalıdır.
✔ Tüm açı ölçüleri eşit olmalıdır.

✅ Örnek:
✔ İki dikdörtgenin tüm kenarları aynıysa, eş dikdörtgendir.
✔ İki kare tüm kenarları eşitse, eş karedir.

3. Eş Şekillerin Özellikleri

✔ Uzunluklar tamamen aynıdır.
✔ Açılar tamamen aynıdır.
✔ Şekillerin yönü farklı olabilir (döndürülmüş olabilir).

🚀 Eğer iki şekil birebir aynıysa, bu şekiller eş şekillerdir!

Benzerlik Nedir?

📌 Tanım:
İki şekil benzer ise, aynı şekle sahiptir ancak farklı boyutlarda olabilir.

✔ Benzer şekillerin açıları birebir aynıdır.
✔ Kenar uzunlukları orantılıdır.
✔ Benzerlik oranı, iki şeklin karşılık gelen kenarlarının oranı ile bulunur.

🚀 Özetle, benzer şekillerin büyütülmüş veya küçültülmüş halleridir.

1. Benzer Üçgenlerin Özellikleri

📌 İki üçgenin benzer olması için aşağıdaki şartlar sağlanmalıdır:

✔ AAA (Açı – Açı – Açı) Benzerliği:

• İki üçgenin tüm açıları eşitse, bu üçgenler benzerdir.

✔ Kenar – Açı – Kenar (KAK) Benzerliği:

• İki üçgenin bir açısı ve bu açının oluşturduğu kenarların oranı aynıysa, üçgenler benzerdir.

✔ Kenar – Kenar – Kenar (KKK) Benzerliği:

• İki üçgenin tüm kenar uzunlukları aynı oranda büyütülmüş veya küçültülmüşse, üçgenler benzerdir.

✅ Örnek:
ABC ve DEF üçgenlerinin açıları şu şekildedir:

✔ ∠A = ∠D
✔ ∠B = ∠E
✔ ∠C = ∠F

Bu üçgenler AAA kuralına göre benzerdir.

✔ Gösterim:

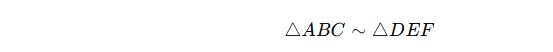
2. Benzer Çokgenlerin Özellikleri

📌 İki çokgenin benzer olması için:
✔ Tüm açıları birebir eşit olmalıdır.
✔ Karşılık gelen kenar uzunlukları aynı oranda olmalıdır.

✅ Örnek:
İki kare, kenarları 4 cm ve 8 cm olan benzer karelerdir.
Benzerlik oranı:

📌 Sonuç: Benzer çokgenlerde kenar uzunlukları belirli bir oranla büyüyüp küçülür.

3. Benzerlik Oranı ve Uygulamaları

✔ Benzerlik oranı, iki şeklin karşılık gelen kenar uzunluklarının oranıdır.

✅ Örnek:
ABC üçgeninin kenarları 6 cm, 8 cm ve 10 cm
DEF üçgeninin kenarları 9 cm, 12 cm ve 15 cm

Benzerlik oranı:

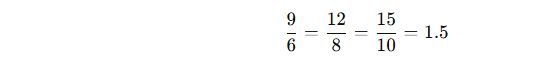
🚀 Sonuç: Bu üçgenler benzer olup, DEF üçgeni ABC üçgeninin 1.5 katı büyütülmüş halidir.

4. Gerçek Hayatta Benzerlik Kullanımı

✔ Harita Çizimlerinde: Küçük ölçekli haritalar, benzerlik prensibi ile hazırlanır.
✔ Gölge Boyu ile Boy Tahmini: Bir ağacın gölge uzunluğu kullanılarak yüksekliği hesaplanabilir.
✔ Fotoğraf Büyütme ve Küçültme: Dijital ortamda görüntüler belirli oranlarla büyütülüp küçültülebilir.

✅ Örnek:
Bir ağacın boyunu hesaplamak için şu benzerlik kullanılır:

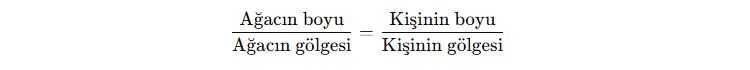
📌 Bu konuda öğrendiklerimiz:
✅ Benzerlik kavramını öğrendik.
✅ Benzer üçgenlerin kurallarını inceledik.
✅ Benzer çokgenlerin özelliklerini öğrendik.
✅ Benzerlik oranının nasıl hesaplandığını öğrendik.
✅ Gerçek hayatta benzerlik prensibinin nasıl kullanıldığını gördük.

Benzerlik Oranı ile İlgili Problemler ve Çözümleri

Benzerlik oranı, iki benzer şeklin karşılık gelen kenar uzunluklarının oranıdır. Bu oranı kullanarak bilinmeyen uzunlukları ve şekil büyüklüklerini hesaplayabiliriz.

1. İki Üçgenin Benzerlik Oranını Bulma

📌 Soru 1:
ABC üçgeninin kenar uzunlukları 6 cm, 9 cm ve 12 cm
DEF üçgeninin kenar uzunlukları 8 cm, 12 cm ve 16 cm

Bu üçgenlerin benzerlik oranı nedir?

2. Benzerlik Oranı ile Kenar Uzunluğu Bulma

📌 Soru 2:
İki benzer üçgenin benzerlik oranı 5:3. Küçük üçgenin bir kenarı 9 cm ise, büyük üçgende karşılık gelen kenar uzunluğu kaç cm’dir?

3. Gölge Yöntemi ile Boy Hesaplama

📌 Soru 3:
Bir ağacın gölge uzunluğu 12 metre, 1.8 metre boyundaki bir insanın gölge uzunluğu 3 metre.
Ağacın yüksekliği kaç metredir?

4. Dikdörtgenin Benzerlik Oranı

📌 Soru 4:
Bir dikdörtgenin uzun kenarı 18 cm, kısa kenarı 12 cm.
Benzer bir dikdörtgenin kısa kenarı 8 cm ise, uzun kenarı kaç cm’dir?

5. Harita Üzerinde Gerçek Mesafe Bulma

📌 Soru 5:
Bir haritada iki şehir arasındaki mesafe 5 cm.
Gerçekte bu şehirler arasındaki mesafe 250 km.
Haritanın ölçeği nedir?

6. Üçgenin Bir Kenarını Benzerlik Oranı ile Bulma

📌 Soru 6:
İki benzer üçgenin benzerlik oranı 2:3.
Büyük üçgende bir kenarın uzunluğu 15 cm ise, küçük üçgendeki karşılık gelen kenar uzunluğu kaç cm’dir?

7. Eşkenar Üçgenin Kenar Uzunluğuna Göre Benzerliği

📌 Soru 7:
Bir eşkenar üçgenin kenarı 9 cm.
Bu üçgenin 1.5 katı büyütülmüş benzer üçgenin kenar uzunluğu kaç cm’dir?

8. Bir Fotoğrafın Orantılı Büyütülmesi

📌 Soru 8:
Bir fotoğrafın boyutları 6 cm x 8 cm.
Bu fotoğraf orantılı şekilde büyütülerek uzun kenarı 20 cm yapılmıştır.
Kısa kenar kaç cm olur?

9. Gerçek Hayatta Benzerlik Oranı Kullanımı (Bayrak Direği Problemi)

📌 Soru 9:
Bir 5 metre uzunluğundaki direğin gölgesi 4 metre.
Yanında duran bir çocuğun gölgesi 2 metre.
Çocuğun boyu kaç metredir?

10. Benzerlik Oranı Kullanarak Bilinmeyen Kenarı Bulma

📌 Soru 10:
İki benzer üçgenin benzerlik oranı 4:5.
Küçük üçgendeki bir kenarın uzunluğu 12 cm ise, büyük üçgendeki karşılık gelen kenar uzunluğu kaç cm’dir?

📌 Bu 10 soru ile şunları öğrendik:
✔ Benzerlik oranı ile bilinmeyen kenar uzunluklarını bulduk.
✔ Gölge uzunlukları ile boy hesaplaması yaptık.
✔ Harita ölçekleri ve orantılı büyütme-küçültme yöntemlerini inceledik.
✔ Fotoğraf boyutlarını orantılı büyütme tekniğiyle hesapladık.
✔ Eşkenar üçgenlerde kenar uzunluğu benzerlik oranına göre hesapladık.

Eşlik ve Benzerlik Konu Özeti

Bu konu boyunca eş ve benzer şekillerin özelliklerini, eşlik ve benzerlik oranlarını, üçgenler ve çokgenlerde benzerlik kurallarını öğrendik. İşte öğrendiklerimizin kısa bir özeti:

1. Eşlik (Congruence) Nedir?

📌 Tanım:
İki şekil eş ise, birebir aynı boyutta ve aynı şekildedir.

✔ Eş şekillerin tüm açıları ve kenar uzunlukları eşittir.
✔ Döndürme, kaydırma veya yansıtma yapıldığında şekiller hâlâ eş kalır.
✔ Eşlik “≅” sembolü ile gösterilir.

Eş Üçgenlerin Özellikleri

İki üçgenin eş olması için şu kurallardan biri sağlanmalıdır:

✔ SSS (Sıra Sıra Üç Kenar Eşitliği):

• Üç kenarı da birbirine eşit olan üçgenler eş üçgendir.

✔ KSK (Kenar – Açı – Kenar Eşitliği):

• İki kenarı ve aralarındaki açı eşit olan üçgenler eş üçgendir.

✔ ASA (Açı – Kenar – Açı Eşitliği):

• İki açısı ve arasındaki kenarı eşit olan üçgenler eş üçgendir.

✔ 90°DK (Dik Kenar – Hipotenüs Eşliği):

• Dik üçgenlerde hipotenüs ve bir dik kenar eşitse, üçgenler eş üçgendir.

📌 Sonuç: Eş üçgenlerin kenar uzunlukları ve açı ölçüleri birebir aynıdır.

2. Benzerlik (Similarity) Nedir?

📌 Tanım:
İki şekil benzer ise, aynı şekle sahiptir ancak farklı boyutlardadır.

✔ Benzer şekillerin açıları birebir aynıdır.
✔ Kenar uzunlukları orantılıdır.
✔ Benzerlik “∼” sembolü ile gösterilir.

Benzer Üçgenlerin Özellikleri

İki üçgenin benzer olması için şu kurallardan biri sağlanmalıdır:

✔ AAA (Açı – Açı – Açı) Benzerliği:

• Üç açısı da eşit olan üçgenler benzerdir.

✔ KAK (Kenar – Açı – Kenar) Benzerliği:

• Bir açısı ve bu açının oluşturduğu iki kenarın oranı aynıysa, üçgenler benzerdir.

✔ KKK (Kenar – Kenar – Kenar) Benzerliği:

• Üç kenar uzunluğu aynı oranda büyütülmüş/küçültülmüşse, üçgenler benzerdir.

📌 Sonuç: Benzer üçgenlerde açı ölçüleri aynıdır, kenarlar belirli bir oranla büyütülür veya küçültülür.

3. Benzerlik Oranı Nedir?

📌 Tanım:
Benzerlik oranı, iki şeklin karşılık gelen kenar uzunluklarının oranıdır.

✔ İki üçgenin benzerlik oranı şu şekilde hesaplanır:

Benzerlik Oranı ile Kenar Uzunluğu Bulma

✅ Örnek:
Benzerlik oranı 3:2, küçük üçgenin bir kenarı 6 cm ise:

İçler dışlar çarpımı:

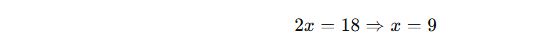
✅ Cevap: Büyük üçgendeki karşılık gelen kenar 9 cm’dir.

📌 Sonuç: Benzerlik oranı kullanılarak bilinmeyen uzunluklar hesaplanabilir.

4. Gerçek Hayatta Benzerlik Kullanımı

✔ Harita Ölçekleri:

• Bir haritadaki 5 cm’lik mesafe 250 km’ye eşitse, ölçek oranı 1:50’dir.

✔ Gölge Yöntemi ile Boy Hesaplama:

✔ Fotoğraf Büyütme ve Küçültme:

• 6 cm x 8 cm’lik bir fotoğraf orantılı şekilde büyütülerek uzun kenarı 20 cm yapılırsa, kısa kenar 15 cm olur.

📌 Sonuç: Benzerlik, günlük hayatta harita ölçekleri, gölge boyu hesaplama ve fotoğraf büyütme gibi birçok alanda kullanılır.

📌 Bu konu kapsamında öğrendiklerimiz:
✅ Eş ve benzer şekiller arasındaki farkları öğrendik.
✅ Eş ve benzer üçgenlerin kurallarını inceledik.
✅ Benzerlik oranının nasıl hesaplandığını öğrendik.
✅ Gerçek hayatta benzerlik oranının nasıl kullanıldığını gördük.