İçindekiler
Geometrik Cisimler Konu Anlatımı
📌 Tanım:
8. Sınıf Matematik Geometrik cisimler, üç boyutlu (3D) şekiller olup, yüzeyleri, köşeleri ve ayrıtları olan nesnelerdir.
✔ Bu cisimler günlük hayatta binalar, kutular, silindirler ve koniler gibi birçok yapıda karşımıza çıkar.
✔ İki boyutlu şekillerin (kare, dikdörtgen, daire vb.) üçüncü boyutta genişlemesiyle oluşurlar.
🚀 Bu konuda şu geometrik cisimleri inceleyeceğiz:
1️⃣ Dik Prizmalar (Dikdörtgenler prizması, küp vb.)
2️⃣ Dik Dairesel Silindir
3️⃣ Dik Piramit
4️⃣ Dik Koni
📌 Bu cisimlerin temel elemanlarını, yüzey alanı ve hacim hesaplamalarını detaylı inceleyeceğiz.
Dik Prizmalar ve Özellikleri
📌 Tanım:
Dik prizma, tabanı çokgen olan ve yan yüzleri dikdörtgenlerden oluşan üç boyutlu bir geometrik cisimdir.
✔ Tabanlar birbirine eş ve paraleldir.
✔ Yan yüzler dikdörtgendir.
✔ Prizma yükseklik boyunca dik olarak uzanır.
🚀 Dik prizmalar günlük hayatta kutular, binalar, dolaplar ve kitaplar gibi birçok yapıda görülür.
1. Dik Prizmanın Temel Elemanları
📌 Bir dik prizma şu temel elemanlardan oluşur:
✔ Tabanlar: Üst ve alt yüzeylerdir, genellikle eş çokgenlerden oluşur.
✔ Yan Yüzler: Tabanları birleştiren dikdörtgen yüzeylerdir.
✔ Köşeler: Yan yüzlerin ve tabanların birleştiği noktalardır.
✔ Ayrıtlar: İki yüzeyin birleştiği çizgilerdir.
✔ Yükseklik (h): İki taban arasındaki dik uzaklıktır.
✅ Örnek: Dikdörtgenler prizmasında:
- 6 yüzü,
- 8 köşesi,
- 12 ayrıtı vardır.
📌 Özel bir dik prizma olan küp, tüm kenarları eşit uzunlukta olan bir dikdörtgenler prizmasıdır.
2. Dik Prizmanın Yüzey Alanı
📌 Yüzey Alanı Formülü:
Dik prizmanın yüzey alanı, tüm yüzeylerinin toplam alanıdır.

3. Dik Prizmanın Hacmi
📌 Hacim Formülü:
Dik prizmanın hacmi, taban alanı ile yüksekliğin çarpımıdır.

4. Dik Prizmanın Açınımı
📌 Açınım, prizmanın yüzeylerinin düzlem üzerine açılarak gösterilmesidir.
✔ Bir dikdörtgenler prizmasının açınımı:
- İki taban (eş çokgenler)
- Dört dikdörtgen şeklinde yan yüzler
✅ Örnek: Küpün açınımı 6 eş kareden oluşur.
5. Günlük Hayatta Dik Prizmalar
✔ Kargo Kutuları: Genellikle dikdörtgenler prizması şeklindedir.
✔ Binalar: Dik prizma şeklinde tasarlanır.
✔ Cep Telefonları ve Laptoplar: Genellikle prizma formundadır.
Dik Dairesel Silindir ve Özellikleri
📌 Tanım:
Dik dairesel silindir, iki paralel daire tabanı olan ve yan yüzü dikdörtgen şeklinde açılanan bir geometrik cisimdir.
✔ Tabanı dairedir.
✔ Yan yüzü kıvrılmış bir dikdörtgendir.
✔ Taban yüzleri birbirine eş ve paraleldir.
✔ Yüksekliği (h), taban merkezlerini birleştiren dik uzaklıktır.
🚀 Silindir, günlük hayatta su şişeleri, borular, teneke kutular gibi birçok yapıda görülür.
1. Dik Dairesel Silindirin Temel Elemanları
📌 Bir silindir şu elemanlardan oluşur:
✔ Tabanlar: Üst ve alt yüzeyler, birbirine eş iki dairedir.
✔ Yükseklik (h): İki taban merkezi arasındaki dik uzaklıktır.
✔ Yarıçap (r): Taban dairesinin merkezden kenara olan uzaklığıdır.
✔ Yan yüz: Düzlemde açıldığında dikdörtgen oluşturur.
✅ Örnek: Bir su şişesi, tabanı daire olan bir dik silindirdir.
2. Dik Dairesel Silindirin Açınımı
📌 Bir dik silindirin açınımı:
✔ İki daire (tabanlar)
✔ Bir dikdörtgen (yan yüz)
✔ Yan yüzün uzunluğu, taban çevresi kadar olur:
![]()
✔ Yan yüz yüksekliği, silindirin yüksekliği kadardır.
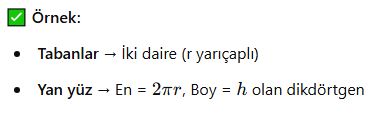
📌 Açınımı çizerken, yan yüzün genişliği tabanın çevresi kadar olur.
3. Dik Dairesel Silindirin Yüzey Alanı
📌 Yüzey Alanı Formülü:
Silindirin yüzey alanı, iki taban alanı ve yan yüz alanının toplamıdır.

✅ Örnek:
Bir silindirin yarıçapı 4 cm, yüksekliği 10 cm ise yüzey alanı nedir?
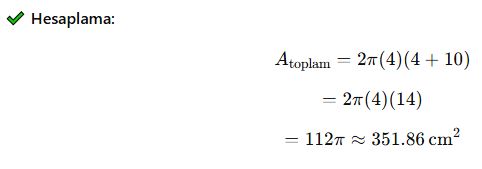
✅ Cevap: Yaklaşık 351.86 cm²’dir.
4. Dik Dairesel Silindirin Hacmi
📌 Hacim Formülü:
Dik silindirin hacmi, taban alanı ile yüksekliğin çarpımıdır.

✅ Örnek:
Bir silindirin yarıçapı 3 cm, yüksekliği 7 cm ise hacmi nedir?
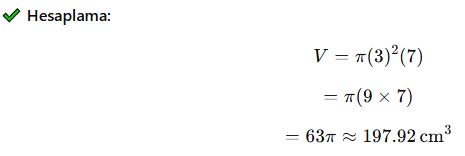
✅ Cevap: Yaklaşık 197.92 cm³’tür.
5. Günlük Hayatta Silindirler
✔ Su Şişeleri: Silindirik formdadır.
✔ Boru ve Tüpler: Gaz tüpleri, borular silindir şeklindedir.
✔ Konserve Kutuları: Marketlerde satılan bazı gıdaların kutuları silindir şeklindedir.
Dik Piramit ve Özellikleri
📌 Tanım:
Dik piramit, bir tabanı olan ve tabanın tam merkezinden tepe noktasına dik bir yükseklik çıkan üç boyutlu geometrik bir cisimdir.
✔ Tabanı çokgen (üçgen, kare, beşgen vb.) olabilir.
✔ Yan yüzleri üçgenlerden oluşur.
✔ Tepe noktası tabanın tam merkezine dik olacak şekilde yer alır.
✔ Piramitin yüksekliği (h), tepe noktasından taban merkezine inen dik uzunluktur.
🚀 Piramitler, özellikle mimari yapılarda ve tarihi anıtlarda sıkça görülür (Mısır Piramitleri gibi).
1. Dik Piramitlerin Temel Elemanları
📌 Bir piramit şu elemanlardan oluşur:
✔ Taban: Çokgen şeklindeki alt yüzeydir.
✔ Yan Yüzler: Üçgenlerden oluşur ve tepe noktasında birleşir.
✔ Ayrıtlar: Yan yüzleri ve tabanı birleştiren kenarlardır.
✔ Tepe Noktası: Yan yüzlerin birleştiği üst noktadır.
✔ Yükseklik (h): Tepe noktasından tabanın merkezine inen dik uzunluktur.
✅ Örnek: Kare tabanlı bir piramit, tabanı kare ve dört adet üçgen yüzeye sahiptir.
2. Dik Piramitlerin Açınımı
📌 Piramitin açınımı, tüm yüzlerinin düzlem üzerinde açılmasıyla elde edilir.
✔ Bir kare tabanlı piramidin açınımı:
- Bir kare (taban yüzü)
- Dört üçgen (yan yüzler)
✅ Örnek: Üçgen tabanlı bir piramit açıldığında bir üçgen ve üç yan yüz üçgeni oluşur.
3. Dik Piramitlerin Yüzey Alanı
📌 Yüzey Alanı Formülü:
Piramitin yüzey alanı, taban alanı ile tüm üçgen yan yüzlerin alanlarının toplamıdır.

4. Dik Piramitlerin Hacmi
📌 Hacim Formülü:
Piramitin hacmi, taban alanı ile yüksekliğin çarpımının üçte biri olarak hesaplanır.

5. Günlük Hayatta Piramitler
✔ Mısır Piramitleri: En ünlü piramit yapılarıdır.
✔ Çadırlar: Genellikle üçgen tabanlı piramit yapısındadır.
✔ Kristal Prizması: Optik deneylerde kullanılan cam prizma da bir piramittir.
Dik Koni ve Özellikleri
📌 Tanım:
Dik koni, bir daire tabanı ve bu tabandan belirli bir yükseklikte bulunan bir tepe noktasının birleşmesiyle oluşan üç boyutlu geometrik bir cisimdir.
✔ Tabanı dairedir.
✔ Yan yüzü kıvrılmış bir üçgendir.
✔ Tepe noktası, tabanın merkezine dik olacak şekilde yer alır.
✔ Koninin yüksekliği (h), tepe noktasından tabanın merkezine inen dik uzunluktur.
🚀 Koni, dondurma külahları, trafik konileri ve şapka gibi birçok nesnede görülür.
1. Dik Koninin Temel Elemanları
📌 Bir dik koni şu elemanlardan oluşur:
✔ Taban: Bir daireden oluşur.
✔ Yan Yüz: Daire şeklindeki tabanı çevreleyen kıvrımlı yüzeydir.
✔ Tepe Noktası: Tüm yan yüzlerin birleştiği üst noktadır.
✔ Yükseklik (h): Tepe noktasından tabanın merkezine inen dik uzunluktur.
✔ Yanal Uzunluk (l): Tepe noktasından tabanın kenarına olan eğik mesafedir.
✔ Yarıçap (r): Taban dairesinin merkezden kenara olan uzaklığıdır.
✅ Örnek: Bir trafik konisi, tabanı daire ve tepe noktası olan bir dik konidir.
2. Dik Koninin Açınımı
📌 Bir koninin açınımı:
✔ Bir daire (taban yüzü)
✔ Bir dairesel sektör (yan yüz)
✔ Yan yüzün uzunluğu, tabanın çevresi kadar olur:
![]()
✔ Yan yüz, açıldığında bir dairesel sektör (dilim) oluşturur.
✅ Örnek:
- Taban: r yarıçaplı bir daire
- Yan yüz: Yarıçapı L olan dairesel bir yay
📌 Açınımı çizerken, yan yüzün yay uzunluğu tabanın çevresi kadar olur.
3. Dik Koninin Yüzey Alanı
📌 Yüzey Alanı Formülü:
Koninin yüzey alanı, taban alanı ile yan yüz alanının toplamıdır.

4. Dik Koninin Hacmi
📌 Hacim Formülü:
Dik koninin hacmi, taban alanı ile yüksekliğin çarpımının üçte biri olarak hesaplanır.

✔ Dondurma Külahları: Üç boyutlu koni şeklindedir.
✔ Trafik Konileri: Yol güvenliği için kullanılan koni şeklindeki nesnelerdir.
✔ Şapkalar: Özellikle doğum günü şapkaları koni formundadır.
✔ Huni: Sıvıları bir kaptan diğerine aktarmak için kullanılan araç koni şeklindedir.
Geometrik Cisimler Konu Özeti
Bu konu boyunca dik prizmalar, dik dairesel silindir, dik piramit ve dik koninin temel elemanlarını, yüzey alanı ve hacim hesaplamalarını öğrendik. İşte öğrendiklerimizin kısa bir özeti:
1. Dik Prizmalar
📌 Tanım:
Dik prizma, tabanı çokgen olan ve yan yüzleri dikdörtgenlerden oluşan üç boyutlu bir geometrik cisimdir.
✔ Tabanlar eş ve paraleldir.
✔ Yan yüzleri dikdörtgendir.
✔ Dik prizmalar günlük hayatta binalar, kutular ve kitaplar gibi yapılarda görülür.

2. Dik Dairesel Silindir
📌 Tanım:
Dik dairesel silindir, iki paralel daire tabanı ve kıvrılmış dikdörtgen bir yan yüzeyi olan üç boyutlu cisimdir.
✔ Tabanlar eş ve paraleldir.
✔ Yan yüzü kıvrılmış bir dikdörtgendir.

3. Dik Piramit
📌 Tanım:
Dik piramit, bir çokgen tabanı ve üçgen yan yüzleri olan, tepe noktası tabanın tam merkezine dik olan üç boyutlu bir cisimdir.
✔ Tabanı üçgen, kare, beşgen vb. olabilir.
✔ Yan yüzleri üçgenlerden oluşur.

4. Dik Koni
📌 Tanım:
Dik koni, bir daire tabanı ve tepe noktasına doğru uzanan yan yüzü olan üç boyutlu bir cisimdir.
✔ Tabanı dairedir.
✔ Yan yüzü kıvrılmış bir üçgendir.
✔ Yüksekliği, tepe noktasından taban merkezine inen dik uzunluktur.

5. Günlük Hayatta Geometrik Cisimler
✔ Dik Prizmalar: Kargo kutuları, binalar, cep telefonları
✔ Silindirler: Su şişeleri, borular, konserve kutuları
✔ Piramitler: Mısır piramitleri, çadırlar, optik prizmalar
✔ Koniler: Dondurma külahları, trafik konileri, şapkalar
📌 Bu konu kapsamında öğrendiklerimiz:
✅ Dik prizma, silindir, piramit ve koninin temel elemanlarını öğrendik.
✅ Bu cisimlerin yüzey alanı ve hacimlerini hesapladık.
✅ Geometrik cisimlerin günlük hayattaki kullanımlarını inceledik.
8. Sınıf Matematik Geometrik Cisimler Çözümlü Örnek Sorular
1. Dikdörtgenler Prizmasının Yüzey Alanı
📌 Soru 1:
Taban kenarları 5 cm ve 8 cm, yüksekliği 12 cm olan bir dikdörtgenler prizmasının toplam yüzey alanını hesaplayınız.
Çözüm:
✔ Yüzey alanı formülü:
![]()
✅ Cevap: Dikdörtgenler prizmasının toplam yüzey alanı 392 cm²’dir.
2. Dikdörtgenler Prizmasının Hacmi
📌 Soru 2:
Taban kenarları 4 cm ve 7 cm, yüksekliği 9 cm olan bir dikdörtgenler prizmasının hacmini hesaplayınız.
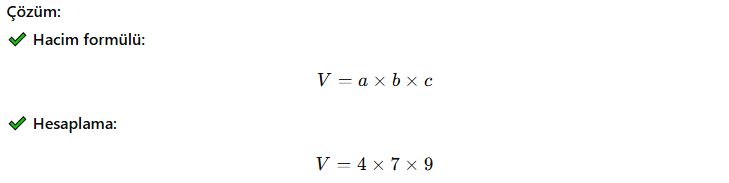
✅ Cevap: Dikdörtgenler prizmasının hacmi 252 cm³’tür.
3. Silindirin Yüzey Alanı
📌 Soru 3:
Yarıçapı 6 cm, yüksekliği 10 cm olan bir silindirin toplam yüzey alanını hesaplayınız.

✅ Cevap: Silindirin toplam yüzey alanı yaklaşık 603.19 cm²’dir.
4. Silindirin Hacmi
📌 Soru 4:
Yarıçapı 5 cm, yüksekliği 12 cm olan bir silindirin hacmini hesaplayınız.

✅ Cevap: Silindirin hacmi yaklaşık 942.48 cm³’tür.
5. Kare Tabanlı Piramidin Hacmi
📌 Soru 5:
Taban kenarı 8 cm, yüksekliği 15 cm olan bir kare tabanlı piramidin hacmini hesaplayınız.
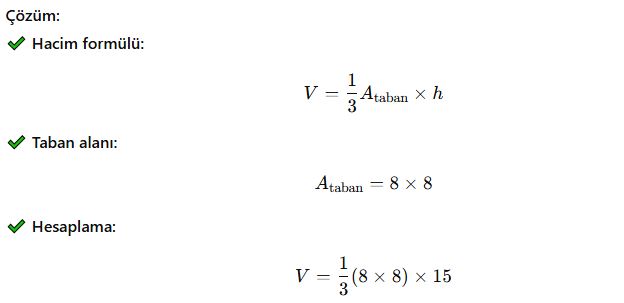
✅ Cevap: Kare tabanlı piramidin hacmi 320 cm³’tür.
6. Dik Koninin Yüzey Alanı
📌 Soru 6:
Yarıçapı 4 cm, yanal uzunluğu 10 cm olan bir dik koninin toplam yüzey alanını hesaplayınız.
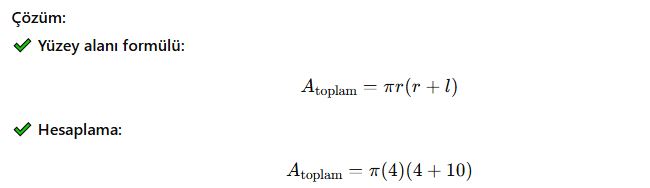
✅ Cevap: Dik koninin toplam yüzey alanı yaklaşık 175.93 cm²’dir.
7. Dik Koninin Hacmi
📌 Soru 7:
Yarıçapı 6 cm, yüksekliği 14 cm olan bir dik koninin hacmini hesaplayınız.
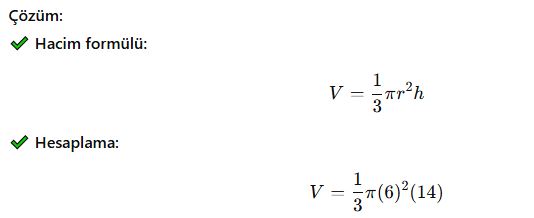
✅ Cevap: Dik koninin hacmi yaklaşık 527.79 cm³’tür.
8. Küpün Yüzey Alanı
📌 Soru 8:
Bir küpün bir kenarının uzunluğu 9 cm ise, küpün toplam yüzey alanını hesaplayınız.

✅ Cevap: Küpün toplam yüzey alanı 486 cm²’dir.
9. Küpün Hacmi
📌 Soru 9:
Bir küpün bir kenar uzunluğu 7 cm ise, küpün hacmini hesaplayınız.

✅ Cevap: Küpün hacmi 343 cm³’tür.
10. Taban Alanı Verilen Piramidin Hacmi
📌 Soru 10:
Taban alanı 64 cm², yüksekliği 18 cm olan bir dik piramidin hacmini hesaplayınız.
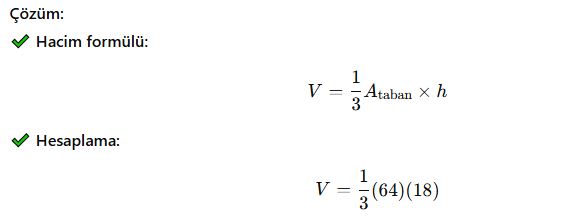
✅ Cevap: Dik piramidin hacmi 384 cm³’tür.
📌 Bu 10 soru ile şunları öğrendik:
✔ Dikdörtgenler prizmasının yüzey alanı ve hacmini hesapladık.
✔ Dik dairesel silindirin yüzey alanı ve hacmini bulduk.
✔ Dik piramit ve dik koninin yüzey alanı ile hacmini hesapladık.
✔ Küpün yüzey alanı ve hacmini öğrendik.
✔ Gerçek hayatta bu geometrik şekillerin nasıl kullanıldığını inceledik.

