Kareköklü ifadeler, matematikte bir sayının hangi sayının karesi olduğunu bulmamızı sağlayan ifadelerdir. Sayıları tam kare ve tam kare olmayan olarak ayırarak, bir sayının karekökünü nasıl hesaplayabileceğimizi öğreniriz. Kareköklü sayılar, özellikle geometri, mühendislik ve bilimsel hesaplamalar gibi birçok alanda kullanılır.

Bu konu kapsamında öncelikle tam kare doğal sayılar ve karekök kavramını inceleyeceğiz. Daha sonra tam kare olmayan sayıların karekökünü nasıl tahmin edeceğimizi, kareköklü ifadelerle işlem yapma kurallarını ve ondalık sayıların kareköklerini ele alacağız. Son olarak gerçek sayılar kavramını, yani rasyonel ve irrasyonel sayıların farklarını öğreneceğiz. Şimdi ilk başlığımız olan “Tam Kare Doğal Sayılar ve Karekökleri” konusunu detaylı bir şekilde ele alalım. 🚀

Tam Kare Doğal Sayılar ve Karekökleri

Matematikte bir sayının karesini almak ve karekökünü bulmak, birçok işlemde karşımıza çıkan önemli kavramlardır. Bu bölümde tam kare doğal sayıları ve karekök kavramını detaylıca inceleyeceğiz.

1. Tam Kare Doğal Sayılar Nedir?

Bir doğal sayı, bir başka doğal sayının karesi olarak yazılabiliyorsa, bu sayıya tam kare doğal sayı denir.

📌 Örnekler:

• 1 = 1 × 1 → 1 tam karedir.
• 4 = 2 × 2 → 4 tam karedir.
• 9 = 3 × 3 → 9 tam karedir.
• 16 = 4 × 4 → 16 tam karedir.
• 25 = 5 × 5 → 25 tam karedir.

Tam kare olmayan doğal sayılar:

• 2, 3, 5, 6, 7, 8, 10, 11, 12, 13… gibi sayılar hiçbir doğal sayının tam karesi değildir.

📌 İlk 15 Tam Kare Doğal Sayı:

$$1,4,9,16,25,36,49,64,81,100,121,144,169,196,225$$

2. Karekök Kavramı

Bir sayının karesini almak, o sayıyı kendisiyle çarpmak demektir. Bunun tersine, bir sayının karekökünü almak ise, hangi sayının karesi olduğunu bulmak anlamına gelir.

📌 Tanım:
Bir sayının karekökü, kendisiyle çarpıldığında o sayıyı veren değerdir.

Matematiksel gösterimi:

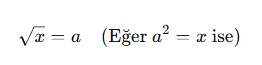
✅ Örnekler:

• √4 = 2 (Çünkü 2 × 2 = 4)
• √9 = 3 (Çünkü 3 × 3 = 9)
• √16 = 4 (Çünkü 4 × 4 = 16)

Pozitif ve Negatif Karekökler

Bir sayının karesi daima pozitif olduğu için tam kare doğal sayıların karekökü pozitif bir sayıdır. Ancak bazı durumlarda negatif sayılarla da karekök alınabilir:

• √25 = 5
• -√25 = -5

📌 Not: Negatif sayıların karekökü yoktur!

• Örneğin: √(-9) tanımlı değildir çünkü hiçbir gerçek sayı kendisiyle çarpıldığında -9’u vermez.

3. Kareköklü Sayıların Özellikleri

✅ Bir tam kare doğal sayının karekökü her zaman tam sayıdır.

• √36 = 6
• √49 = 7
• √100 = 10

✅ Tam kare olmayan sayılar irrasyonel olabilir.

• √2 ≈ 1.414… (Ondalıklı bir sayı)
• √3 ≈ 1.732…

✅ Kök içindeki sayılar çarpma işlemiyle ayrılabilir.

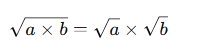
• Örnek: √36 = √9 × √4 = 3 × 2 = 6

✅ Kök içindeki tam kare sayılar dışarı çıkabilir.

• √81 = 9 çünkü 9 × 9 = 81
• √144 = 12 çünkü 12 × 12 = 144

4. Kareköklü Sayıların Günlük Hayattaki Kullanımı

📌 Karekökler, birçok alanda kullanılır:

• Mühendislikte: Alan hesaplamaları, elektrik devreleri
• Fizikte: Kuvvet hesaplamaları
• Geometri: Pisagor Teoremi
• Bilimsel hesaplamalar: Ölçümler, istatistikler

✅ Örnek:
Bir kare şeklindeki bahçenin alanı 49 m² ise, bahçenin bir kenar uzunluğu kaç metredir?

✅ Cevap: Bahçenin bir kenarı 7 metredir.

📌 Bu konuda öğrendiklerimiz:
✅ Tam kare doğal sayıların ne olduğunu öğrendik.
✅ Bir sayının karekökünü nasıl bulacağımızı inceledik.
✅ Kareköklü ifadelerin özelliklerini ve gerçek hayattaki kullanım alanlarını gördük.

Tam Kare Olmayan Sayıların Karekökünü Tahmin Etme

Tam kare olmayan doğal sayıların karekökü, tam sayı olarak ifade edilemez. Ancak bu tür sayıların karekökünü yaklaşık olarak tahmin edebiliriz. Bu konu, ondalık sayıların kareköklerini anlamamıza ve gerçek hayat problemlerini çözmemize yardımcı olur.

1. Tam Kare Olmayan Sayılar ve Karekökleri

Bir sayı tam kare değilse, karekökü irrasyonel bir sayı olur. İrrasyonel sayılar, ondalıklı olarak sonsuza kadar devam eden ve tekrar etmeyen sayılardır.

📌 Örnekler:

• √2 ≈ 1.414
• √3 ≈ 1.732
• √5 ≈ 2.236
• √7 ≈ 2.645

Bu tür sayıların karekökünü tahmin ederek yaklaşık değerlerini bulabiliriz.

2. Tahmin Yöntemi: En Yakın Tam Kareleri Kullanma

Tam kare olmayan bir sayının karekökünü iki tam kare arasında bularak yaklaşık değerini tahmin edebiliriz.

📌 Adımlar:

1. Sayının hangi iki tam kare arasında olduğunu bulun.
2. Bu tam karelerin kareköklerini belirleyin.
3. Hangi sayıya daha yakınsa ona göre yaklaşık bir değer belirleyin.

✅ Örnek 1: √20’yi tahmin edelim.

• 20, 16 ile 25 arasında bir sayıdır.
• 16 = 4² ve 25 = 5² olduğuna göre, √20, 4 ile 5 arasındadır.
• 20, 16’ya mı yoksa 25’e mi daha yakın?
  • 20, 16’dan 4 fazla, 25’ten 5 eksik olduğu için yaklaşık olarak 4.5 alınabilir.

✅ Sonuç: √20 ≈ 4.47

✅ Örnek 2: √50’yi tahmin edelim.

• 50, 49 ile 64 arasında bir sayıdır.
• 49 = 7² ve 64 = 8² olduğuna göre, √50, 7 ile 8 arasındadır.
• 50, 49’a çok yakın olduğu için yaklaşık olarak 7.1 alınabilir.

✅ Sonuç: √50 ≈ 7.07

3. Ondalık Kesirlerle Tahmin Etme

Bazen tam kare olmayan sayıların karekökünü daha hassas bir şekilde tahmin etmek gerekir. Bunun için:

1. Kareköklü ifadeyi iki tam kare arasında buluruz.
2. Daha yakın olduğu tam kareye göre bir tahmin yaparız.
3. Gerekirse hesap makinesiyle kontrol ederiz.

✅ Örnek 3: √72’yi tahmin edelim.

• 72, 64 ile 81 arasındadır.
• 64 = 8² ve 81 = 9² olduğuna göre, √72, 8 ile 9 arasındadır.
• 72, 64’e göre daha büyük, 81’e göre daha küçük olduğu için yaklaşık olarak 8.5 alınabilir.

✅ Sonuç: √72 ≈ 8.49

4. Gerçek Hayatta Kullanımı

📌 Örnek:
Bir kare şeklindeki bahçenin alanı 27 m² ise, kenar uzunluğu kaç metreye yakındır?

• 27, 25 ile 36 arasındadır.
• √25 = 5 ve √36 = 6 olduğuna göre, √27, 5 ile 6 arasındadır.
• **27, 25’e daha yakın olduğu için yaklaşık 5.2 m olarak tahmin edebiliriz.

✅ Cevap: Bahçenin kenarı yaklaşık 5.2 metredir.

5. Daha Hassas Tahmin İçin Bölme Yöntemi

Daha hassas tahmin yapmak için ikiye bölme yöntemi kullanılabilir.
📌 Örnek: √10’u tahmin edelim.

• 10, 9 ile 16 arasındadır.
• 9’un karekökü 3, 16’nın karekökü 4’tür.
• 10, 9’a daha yakın olduğu için yaklaşık olarak 3.1 kabul edilebilir.

✅ Sonuç: √10 ≈ 3.16

📌 Bu konuda öğrendiklerimiz:
✅ Tam kare olmayan sayıların kareköklerinin nasıl tahmin edileceğini öğrendik.
✅ Yakın tam kareleri kullanarak yaklaşık değerler bulduk.
✅ Gerçek hayatta kareköklerin kullanımına örnekler verdik.

a√b Şeklinde Yazma ve Katsayıyı Kök İçine Alma

Kareköklü ifadeleri farklı şekillerde ifade etmek, işlemleri kolaylaştırır. Bu bölümde kareköklü sayıları a√b formuna çevirme ve katsayıyı kök içine alma yöntemlerini detaylıca inceleyeceğiz.

1. Kareköklü Sayıları a√b Şeklinde Yazma

Bir kareköklü sayıyı tam kare çarpanlarını ayırarak daha sade bir hale getirebiliriz.

📌 Kural:

Burada tam kare olan sayı kök dışına çıkar, geriye kalan sayı kök içinde kalır.

✅ Örnekler:

• √50 = √(25 × 2) = √25 × √2 = 5√2
• √72 = √(36 × 2) = √36 × √2 = 6√2
• √200 = √(100 × 2) = √100 × √2 = 10√2

📌 Adım Adım Örnek:
√98’i a√b şeklinde yazalım.

1. 98’i tam kare çarpanlarına ayıralım:
   • 98 = 49 × 2
2. Kök içindeki tam kareyi dışarı çıkaralım:
   • √98 = √49 × √2 = 7√2
     ✅ Sonuç: √98 = 7√2

2. Katsayıyı Kök İçine Alma

Bazı durumlarda kök dışındaki katsayıyı kök içine almak işlemi daha kolay hale getirebilir.

📌 Kural:

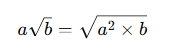
✅ Örnekler:

• 5√3 = √(5² × 3) = √25 × 3 = √75
• 2√7 = √(2² × 7) = √4 × 7 = √28
• 4√5 = √(4² × 5) = √16 × 5 = √80

📌 Adım Adım Örnek:
3√6’yı kök içine alalım.

1. Katsayının karesini alalım:
   • 3² = 9
2. Kök içindeki sayı ile çarpalım:
   • 9 × 6 = 54
3. Sonuç:
   • 3√6 = √54
     ✅ Sonuç: 3√6 = √54

3. a√b Şeklinde Yazma ve Katsayıyı Kök İçine Alma Arasındaki İlişki

Bir kareköklü ifadeyi a√b şeklinde yazabilir veya katsayıyı kök içine alarak tekrar yazabiliriz.

📌 Örnek:
6√2’yi kök içine alalım.

1. Katsayının karesini alalım:
   • 6² = 36
2. Kök içindeki sayı ile çarpalım:
   • 36 × 2 = 72
     ✅ Sonuç: 6√2 = √72

4. Gerçek Hayatta Kullanımı

Kareköklü ifadeleri a√b formunda yazmak, geometri ve fizik hesaplamalarında kullanılır.

📌 Örnek:
Bir kare bahçenin alanı 50 m² ise, kenar uzunluğu kaç metreye yakındır?

Bu ifade, bazen 5√2 olarak bırakılır, bazen yaklaşık değer olarak hesaplanır (yaklaşık 7.07 metre).

📌 Bu konuda öğrendiklerimiz:
✅ Kareköklü ifadeleri a√b formatında nasıl yazacağımızı öğrendik.
✅ Katsayıyı kök içine nasıl alacağımızı öğrendik.
✅ Gerçek hayatta kullanım alanlarını inceledik.

Kareköklü İfadelerde Çarpma ve Bölme İşlemleri

Kareköklü sayılarla işlem yaparken çarpma ve bölme kurallarını bilmek, işlemleri daha hızlı ve doğru yapmamızı sağlar. Bu bölümde kareköklü ifadelerle çarpma ve bölme işlemlerini adım adım inceleyeceğiz.

1. Kareköklü Sayılarla Çarpma İşlemi

📌 Kural:

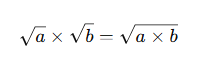
• Aynı kök içinde yazılabilir.
• Tam kare çarpan varsa dışarı çıkartılabilir.

✅ Örnekler:

1. √2 × √8
   • √(2 × 8) = √16 = 4
   • ✅ Cevap: 4
2. √3 × √12
   • √(3 × 12) = √36
   • √36 = 6
   • ✅ Cevap: 6
3. √5 × √10
   • √(5 × 10) = √50
   • √50 = 5√2
   • ✅ Cevap: 5√2

📌 Özel Durum:

• Kareköklü bir sayı, tam sayı ile çarpılırsa çarpma işlemi yalnızca katsayıya uygulanır.

✅ Örnek:
3 × √5 = 3√5

2. Kareköklü Sayılarla Bölme İşlemi

📌 Kural:

• Bölme işlemi kök içine alınabilir.
• Tam kare çarpan varsa dışarı çıkartılabilir.

✅ Örnekler:

1. √18 ÷ √2
   • √(18 ÷ 2) = √9
   • √9 = 3
   • ✅ Cevap: 3

2. √48 ÷ √3
   • √(48 ÷ 3) = √16
   • √16 = 4
   • ✅ Cevap: 4

3. √50 ÷ √2
   • √(50 ÷ 2) = √25
   • √25 = 5
   • ✅ Cevap: 5

📌 Özel Durum:

• Bir kareköklü sayı tam bir sayıya bölünürse sadece katsayı bölünür.

✅ Örnek:
6√18 ÷ 3 = 2√18

3. Kök İçindeki Sayıyı Sadeleştirme (Rasyonelleştirme)

Eğer bölme işleminde köklü sayı paydaya gelirse, payda rasyonel hale getirilmelidir. Bu işleme rasyonelleştirme denir.

📌 Kural:
Bir kesirin paydasında karekök varsa, payda aynı karekökle çarpılarak rasyonelleştirilir.

4. Gerçek Hayatta Kullanımı

Kareköklü ifadelerin çarpma ve bölme kuralları, geometri, mühendislik ve fizik hesaplamalarında sıkça kullanılır.

📌 Örnek:
Bir üçgenin iki kenarı 3√2 m ve 4√3 m ise, üçgenin alanı kaç m²’dir?

• Alan formülü: A = (1/2) × taban × yükseklik
• A = (1/2) × (3√2) × (4√3)
• A = (1/2) × (12√6) = 6√6 m²

✅ Cevap: 6√6 m²

📌 Bu konuda öğrendiklerimiz:
✅ Kareköklü ifadelerde çarpma ve bölme işlemlerini öğrendik.
✅ Bölme işleminde rasyonelleştirme nasıl yapılır öğrendik.
✅ Gerçek hayatta kareköklü ifadelerle hesaplamaların nasıl yapıldığını inceledik.

Kareköklü İfadelerde Toplama ve Çıkarma İşlemleri

Kareköklü ifadelerde toplama ve çıkarma işlemleri, üslü ifadelerle olduğu gibi belirli kurallara göre yapılır. Bu işlemleri yapabilmek için kareköklü ifadelerin benzer olup olmadığını bilmemiz gerekir.

1. Kareköklü Sayılarda Toplama ve Çıkarma Kuralları

📌 Kural:
Benzer köklü ifadeler toplanabilir veya çıkarılabilir.

Benzer köklü ifadeler, kök içindeki sayıları aynı olan ifadelerdir. Bu ifadelerde sadece katsayılar toplanır veya çıkarılır.

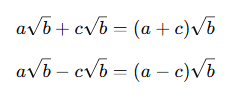
✅ Örnekler:

1. 2√3 + 5√3 = (2+5)√3 = 7√3
2. 4√2 – 3√2 = (4-3)√2 = 1√2 = √2
3. 7√5 + 2√5 – 3√5 = (7+2-3)√5 = 6√5

📌 Özel Durum:

• Kök içleri farklı olan sayılar toplanamaz veya çıkarılamaz!
  • Örnek: 3√2 + 4√5 ≠ 7√(2+5) ❌ (İşlem yapılamaz)

2. Benzer Olmayan Kareköklü Sayıları Toplamadan Önce Dönüştürme

Eğer köklü ifadeler farklıysa, bazı durumlarda kök içindeki tam kareleri ayırarak benzer hale getirilebilirler.

✅ Örnekler:

1. √50 + √18
   • √50 = 5√2, √18 = 3√2
   • 5√2 + 3√2 = (5+3)√2 = 8√2
   • ✅ Sonuç: 8√2
2. √72 – √32
   • √72 = 6√2, √32 = 4√2
   • 6√2 – 4√2 = (6-4)√2 = 2√2
   • ✅ Sonuç: 2√2

3. Farklı Kökleri Aynı Hale Getirme

Bazı köklü ifadeler, farklı görünse de daha sade hale getirildiğinde benzer hale gelebilir.

✅ Örnek:
√75 + 2√12 – 3√3 işlemini yapalım.

1. √75 = 5√3, √12 = 2√3
2. 5√3 + 2(2√3) – 3√3
3. 5√3 + 4√3 – 3√3 = (5+4-3)√3
4. Sonuç: 6√3

4. Gerçek Hayatta Kullanımı

📌 Örnek:
Bir üçgenin iki kenarı √18 cm ve √50 cm ise, üçüncü kenarın uzunluğu √72 cm’dir.
Toplam kenar uzunluğu kaç cm’dir?

1. √18 = 3√2, √50 = 5√2, √72 = 6√2
2. 3√2 + 5√2 + 6√2 = (3+5+6)√2 = 14√2

✅ Sonuç: Üçgenin toplam kenar uzunluğu 14√2 cm’dir.

📌 Bu konuda öğrendiklerimiz:
✅ Benzer köklü ifadelerin nasıl toplanıp çıkarılacağını öğrendik.
✅ Farklı köklü ifadeleri nasıl sadeleştirebileceğimizi gördük.
✅ Gerçek hayatta kullanımına örnekler verdik.

Ondalık İfadelerin Karekökü

Bazı kareköklü sayılar ondalık olarak ifade edilir ve tam sayı sonucuna ulaşmak her zaman mümkün olmayabilir. Bu bölümde, ondalık sayıların karekökünü hesaplama yöntemlerini inceleyeceğiz.

1. Tam Kare Olan Ondalık Sayıların Karekökü

Eğer bir ondalık sayı tam kare bir sayının ondalık hali ise, karekökü tam sayı veya ondalıklı bir sayı olarak bulunabilir.

📌 Örnekler:

• 0,01 = (0,1 × 0,1) → √0,01 = 0,1
• 0,25 = (0,5 × 0,5) → √0,25 = 0,5
• 1,44 = (1,2 × 1,2) → √1,44 = 1,2

📌 Genel Kural:

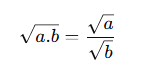
(Eğer hem pay hem payda tam kare ise)

✅ Örnek:

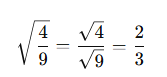
✅ Örnek:

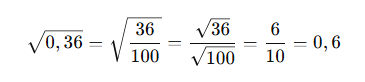
2. Tam Kare Olmayan Ondalık Sayıların Karekökünü Tahmin Etme

Eğer bir ondalık sayı tam kare değilse, karekökü yaklaşık olarak tahmin edilebilir.

📌 Örnek:
√0,3’ü tahmin edelim.

• 0,3 sayısı 0,25 (0,5²) ile 0,36 (0,6²) arasındadır.
• Bu yüzden √0,3 ≈ 0,55 olarak tahmin edilir.

✅ Örnekler:

• √0,5 ≈ 0,707
• √0,7 ≈ 0,836
• √1,5 ≈ 1,225

📌 Tam Kare Olmayan Sayılar İçin Yaklaşık Kural:
Eğer bir sayı x ile y arasında ise,

şeklinde yaklaşık bir sonuç bulunabilir.

✅ Örnek:
√7,2’yi tahmin edelim.

• 7,2 → 4 ile 9 arasındadır.
• √4 = 2 ve √9 = 3 olduğu için √7,2 ≈ 2,6 olarak tahmin edilebilir.

3. Ondalık Sayıları Kesir Haline Getirerek Karekök Alma

Eğer ondalıklı bir sayıyı kesir olarak ifade edebilirsek, karekök işlemi daha kolay hale gelir.

📌 Örnek:
0,04 sayısını kesir olarak ifade edelim:

✅ Örnek:

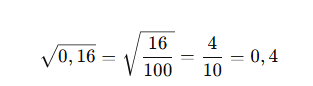
📌 Kesire Çevirerek Yaklaşık Kök Bulma:

1. Sayıyı kesir halinde yaz.
2. Kesrin kökünü al (eğer mümkünse).
3. Kesiri yaklaşık bir ondalık sayı olarak yaz.

✅ Örnek:
√0,75’yi bulalım.

1. 0,75 = 75/100 = 3/4
2. √(3/4) = √3 / √4 = √3 / 2
3. √3 ≈ 1,732 olduğu için:

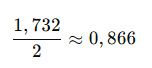
✅ Sonuç: √0,75 ≈ 0,866

4. Gerçek Hayatta Kullanımı

Karekök işlemleri finans, mühendislik, fizik ve istatistik gibi birçok alanda kullanılır.

📌 Örnek:
Bir kare şeklindeki bir masa 0,64 m² alana sahipse, bir kenar uzunluğu kaç metredir?

✅ Cevap: Masanın bir kenarı 0,8 metredir.

📌 Bu konuda öğrendiklerimiz:
✅ Ondalık sayıların karekökünü nasıl hesaplayacağımızı öğrendik.
✅ Tam kare olmayan ondalık sayıların karekökünü tahmin ettik.
✅ Kesir haline getirerek karekök alma yöntemini öğrendik.
✅ Gerçek hayattaki uygulamalarına baktık.

Gerçek Sayılar (Rasyonel ve İrrasyonel Sayılar)

Matematikte gerçek sayılar (ℝ), rasyonel ve irrasyonel sayıların birleşiminden oluşur. Tam sayılar, kesirler, ondalıklı sayılar ve karekök içeren sayılar bu kümede yer alır.

Bu bölümde, rasyonel ve irrasyonel sayıların tanımını, özelliklerini ve farklarını detaylıca inceleyeceğiz.

1. Gerçek Sayılar Kümesi (ℝ) Nedir?

Gerçek sayılar, sayı doğrusu üzerinde gösterilebilen tüm sayıları kapsar. Rasyonel ve irrasyonel sayılar, gerçek sayılar kümesinin iki alt kümesidir.

📌 Gerçek Sayılar Kümesi:

• ℚ → Rasyonel sayılar
• ℚ’ → İrrasyonel sayılar

✅ Örnekler:

• Rasyonel Sayılar: -3, 0, 1, 1.5, ⅔, 0.75, 4, -5
• İrrasyonel Sayılar: √2, π, e, √3, 0.1010010001…

2. Rasyonel Sayılar (ℚ)

📌 Tanım: Kesir olarak yazılabilen sayılara rasyonel sayılar denir.

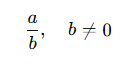
a ve b tam sayı olmak koşuluyla, b sıfırdan farklı bir tam sayı olmalıdır.

✅ Örnekler:

• Tam sayılar: -2, -1, 0, 1, 2, 3…
• Kesirli sayılar: 3/4, 5/2, -7/3
• Sonlu ve devirli ondalıklı sayılar:
  • 0,5 = ½
  • 0,75 = ¾
  • 1,333… = 4/3

📌 Özellikler:

• Kesir olarak yazılabilirler.
• Sonlu veya periyodik (devreden) ondalık gösterime sahiptirler.
• Tam sayılar, doğal sayılar ve kesirli sayılar bu kümede yer alır.

✅ Örnek:
0,666… = ⅔ → Kesir olarak yazılabildiği için rasyoneldir.

3. İrrasyonel Sayılar (ℚ’)

📌 Tanım: Kesir olarak yazılamayan, ondalık gösterimi sonsuz ve düzensiz olan sayılara irrasyonel sayılar denir.

✅ Örnekler:

• Karekök içinde tam kare olmayan sayılar:
  • √2 ≈ 1.414213…
  • √3 ≈ 1.732050…
  • √5 ≈ 2.236067…
• Matematiksel sabitler:
  • π (pi) = 3.1415926535…
  • e (Euler sayısı) = 2.7182818284…
• Sonsuz ve düzensiz ondalıklı sayılar:
  • 0.1010010001…

📌 Özellikler:

• Kesir olarak yazılamazlar.
• Ondalık gösterimleri ne sonlu ne de devirli değildir.
• Matematikte birçok önemli sabit bu kümede yer alır.

✅ Örnek:
√7 = 2.645751311… → Kesirli olarak yazılamadığı için irrasyoneldir.

4. Rasyonel ve İrrasyonel Sayıların Farkları

5. Gerçek Sayılar Kümesinin Alt Küme İlişkisi

📌 Gerçek Sayılar Kümesi (ℝ) şunları içerir:

1. Doğal Sayılar (ℕ): 0, 1, 2, 3, 4…
2. Tam Sayılar (ℤ): …, -3, -2, -1, 0, 1, 2, 3…
3. Rasyonel Sayılar (ℚ): Tam sayılar + Kesirler
4. İrrasyonel Sayılar (ℚ’): Kesir olarak yazılamayan sayılar (√2, π, e, √3)

📌 Genel Küme İlişkisi:

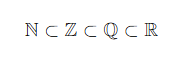
6. Gerçek Hayatta Kullanımı

Rasyonel ve irrasyonel sayılar günlük hayatta birçok alanda kullanılır:

📌 Örnekler:

• Mühendislik: Kareköklü işlemler, devre hesaplamaları
• Fizik: Hız, ivme, dalga boyları
• Ekonomi: Faiz hesaplamaları (irrasyonel sayılar)
• Geometri: Pisagor Teoremi’nde √2 ve √3 gibi irrasyonel sayılar kullanılır.

✅ Örnek:
Bir karenin köşegen uzunluğu √2 katına çıkar.

• Eğer kare kenarı 5 cm ise, köşegen uzunluğu:

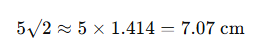
📌 Bu konuda öğrendiklerimiz:
✅ Gerçek sayılar kümesini ve alt kümelerini öğrendik.
✅ Rasyonel ve irrasyonel sayıların farklarını inceledik.
✅ Gerçek hayatta kullanım alanlarını gördük.

8. Sınıf Matematik Kareköklü İfadeler Örnek Sorular ve Çözümleri

1. Rasyonel Sayı mı, İrrasyonel Sayı mı?

📌 Soru 1: Aşağıdaki sayılardan hangisi irrasyonel bir sayıdır?

A) 3/4
B) 0,75
C) √5
D) -2

Çözüm:

• 3/4 → Kesir olarak yazılabildiği için rasyoneldir.
• 0,75 → Sonlu bir ondalık sayı olduğu için rasyoneldir.
• √5 → Karekök içinde tam kare olmayan bir sayı olduğu için irrasyoneldir. ✅
• -2 → Tam sayı olduğu için rasyoneldir.

✅ Cevap: C) √5

2. Devirli Ondalık Sayılar Rasyonel midir?

📌 Soru 2: 0,272727… sayısı rasyonel mi irrasyonel mi?

Çözüm:

• Sayının ondalık kısmı 272727… şeklinde periyodik (devreden) bir sayıdır.
• Devirli ondalık sayılar kesir şeklinde yazılabildiği için rasyonel sayıdır. ✅

✅ Cevap: Rasyonel

3. Hangi Sayı İrrasyoneldir?

📌 Soru 3: Aşağıdaki sayılardan hangisi irrasyonel bir sayıdır?

A) π
B) 2,5
C) 1/3
D) 4,121212…

Çözüm:

• π → Sonsuz ve düzensiz bir ondalık sayı olduğu için irrasyoneldir. ✅
• 2,5 → Sonlu bir ondalık sayı olduğu için rasyoneldir.
• 1/3 → Kesir olarak yazılabildiği için rasyoneldir.
• 4,121212… → Devirli bir sayı olduğu için rasyoneldir.

✅ Cevap: A) π

4. Sayı Gerçek Sayılar Kümesine Ait mi?

📌 Soru 4: -√9 sayısı hangi sayı kümesine aittir?

Çözüm:

• √9 = 3 olduğu için -√9 = -3 olur.
• -3 → Tam sayıdır ve aynı zamanda rasyoneldir.
• Tüm rasyonel sayılar gerçek sayılar kümesine aittir. ✅

✅ Cevap: Rasyonel ve Gerçek Sayılar (ℚ ⊂ ℝ)

5. Sayının Karekökü Rasyonel mi?

📌 Soru 5: √16 rasyonel midir irrasyonel mi?

Çözüm:

• √16 = 4, tam sayı olduğu için rasyoneldir. ✅

✅ Cevap: Rasyonel

6. İrrasyonel Sayının Yaklaşık Değeri

📌 Soru 6: √2’nin yaklaşık değeri kaçtır?

A) 1,3
B) 1,41
C) 1,5
D) 2,0

Çözüm:

• √2 ≈ 1.414 olarak bilinir.
• En yakın değer 1,41’dir. ✅

✅ Cevap: B) 1,41

7. Sayı Rasyonel mi?

📌 Soru 7: Aşağıdaki sayılardan hangisi rasyoneldir?

A) π
B) √11
C) -0,25
D) √7

Çözüm:

• π → Kesir olarak yazılamaz, irrasyoneldir.
• √11 → Tam kare olmayan sayı olduğu için irrasyoneldir.
• -0,25 → Kesir olarak yazılabilir (-1/4), rasyoneldir. ✅
• √7 → Karekök içinde tam kare olmayan sayı olduğu için irrasyoneldir.

✅ Cevap: C) -0,25

8. Sayı Hangi Kümede Yer Alır?

📌 Soru 8: Aşağıdaki sayılardan hangisi ℚ kümesine aittir?

A) 0,333…
B) √5
C) π
D) √3

Çözüm:

• 0,333… → 1/3 olarak yazılabilir, yani rasyoneldir. ✅
• √5 → Tam kare olmayan sayı olduğu için irrasyoneldir.
• π → Sonsuz ve düzensiz bir sayı olduğu için irrasyoneldir.
• √3 → Tam kare olmadığı için irrasyoneldir.

✅ Cevap: A) 0,333…

9. İrrasyonel ve Rasyonel Sayılar Arasındaki Fark

📌 Soru 9: Aşağıdaki ifadelerden hangisi doğrudur?

A) Tüm kareköklü sayılar irrasyoneldir.
B) Tüm devirli ondalık sayılar irrasyoneldir.
C) Tam kare olmayan sayıların karekökü irrasyoneldir.
D) Kesirli sayılar irrasyoneldir.

Çözüm:

• A) Yanlış → √4 gibi bazı kareköklü sayılar tam kare olduğu için rasyoneldir.
• B) Yanlış → 0,333… gibi devirli ondalık sayılar rasyoneldir.
• C) Doğru → Örneğin, √2, √3 gibi sayılar irrasyoneldir. ✅
• D) Yanlış → 3/4 gibi kesirli sayılar rasyoneldir.

✅ Cevap: C) Tam kare olmayan sayıların karekökü irrasyoneldir.

10. Gerçek Sayılar Kümesi İçinde Alt Küme İlişkisi

📌 Soru 10: Aşağıdaki sayı kümeleri nasıl sıralanır?

A) ℕ ⊂ ℤ ⊂ ℚ ⊂ ℝ
B) ℚ ⊂ ℤ ⊂ ℕ ⊂ ℝ
C) ℝ ⊂ ℚ ⊂ ℕ ⊂ ℤ
D) ℕ ⊂ ℝ ⊂ ℚ ⊂ ℤ

Çözüm:

• Doğal sayılar (ℕ), tam sayıların (ℤ) alt kümesidir.
• Tam sayılar, rasyonel sayıların (ℚ) alt kümesidir.
• Rasyonel sayılar, gerçek sayıların (ℝ) alt kümesidir.

✅ Cevap: A) ℕ ⊂ ℤ ⊂ ℚ ⊂ ℝ

📌 10 soru boyunca şunları öğrendik:
✔ Gerçek sayıların hangi kümelere ait olduğunu belirledik.
✔ Rasyonel ve irrasyonel sayıların farkını gördük.
✔ Ondalık gösterimleri inceleyerek rasyonel olup olmadıklarını bulduk.
✔ Gerçek sayıların alt küme ilişkisini inceledik.