Üçgen, üç kenarı ve üç açısı olan kapalı bir geometrik şekildir. Düzlemsel bir şekil olup matematikte, mühendislikte ve günlük hayatta birçok alanda kullanılır. Bir üçgenin en önemli özelliklerinden biri, iç açılarının toplamının her zaman 180° olmasıdır.
İçindekiler
8. Sınıf Matematik Üçgenler Konu Anlatımı
Üçgenler, kenar uzunluklarına ve açılarına göre farklı türlere ayrılır. Ayrıca, üçgenin kenarları ve açıları arasında özel ilişkiler bulunur. Pisagor Teoremi gibi kurallar, üçgenlerin kenarlarını hesaplamada kullanılır. 8. Sınıf Matematik Üçgenler kapsamında üçgenin temel elemanlarını, türlerini ve üçgenle ilgili temel kuralları öğreneceğiz.
Üçgenin Temel Elemanları
Bir üçgen, üç kenar, üç köşe ve üç açıdan oluşan kapalı bir geometrik şekildir. Üçgeni oluşturan elemanları tanıyarak, üçgenin temel özelliklerini daha iyi anlayabiliriz.
Bu bölümde, üçgenin kenarları, köşeleri, açıları, yükseklikleri, açıortayları ve kenarortayları gibi temel bileşenleri inceleyeceğiz. 🚀
1. Üçgenin Temel Bileşenleri
✔ Kenarlar: Üçgeni oluşturan üç doğru parçasıdır.
✔ Köşeler: İki kenarın birleştiği üç noktadır.
✔ Açılar: Üçgenin iç açılarının toplamı 180°’dir.
✅ Örnek:
Aşağıdaki üçgende:
- Kenarlar: [AB], [BC], [CA]
- Köşeler: A, B, C
- Açılar: ∠A, ∠B, ∠C
2. Üçgende Yükseklik
📌 Tanım:
Bir üçgende bir köşeden karşı kenara (veya uzantısına) inilen dik doğru parçasına “yükseklik” denir.
✔ Bir üçgende 3 yükseklik bulunur.
✔ Yükseklikler bir noktada kesişir, bu noktaya “diklik merkezi” denir.
✅ Örnek:
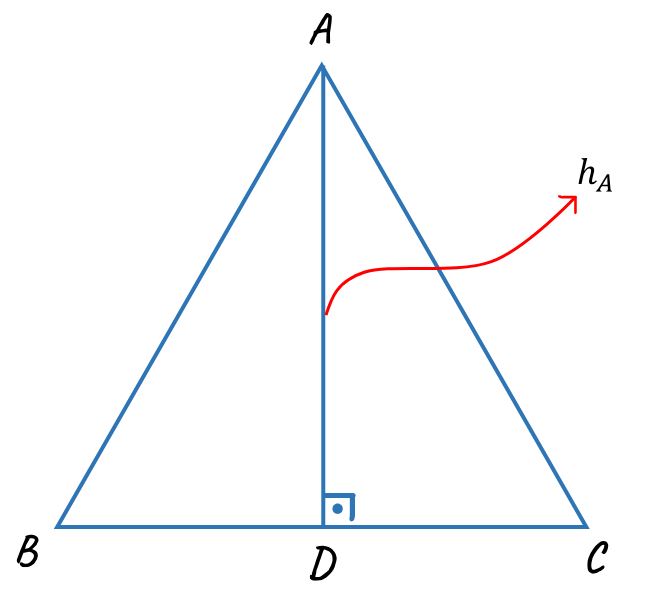
Burada [AH] yüksekliği olup, BC kenarına diktir (90°).
📌 Önemli Bilgi: Üçgenin çeşidine göre yükseklik iç bölgede veya dış bölgede olabilir.
3. Üçgende Açıortay
📌 Tanım:
Bir üçgenin bir köşesindeki açıyı iki eş parçaya bölen doğru parçasına “açıortay” denir.
✔ Bir üçgende 3 açıortay vardır.
✔ Açıortaylar bir noktada kesişir, bu noktaya “iç teğet çember merkezi” denir.
✅ Örnek:

Burada [AN] açıortayı, ∠A açısını iki eş parçaya böler.
📌 Önemli Bilgi: Açıortaylar üçgenin iç teğet çemberinin merkezini belirler.
4. Üçgende Kenarortay
📌 Tanım:
Bir üçgenin bir köşesinden karşı kenarın tam ortasına çizilen doğru parçasına “kenarortay” denir.
✔ Bir üçgende 3 kenarortay vardır.
✔ Kenarortaylar bir noktada kesişir, bu noktaya “ağırlık merkezi” denir.
✅ Örnek:
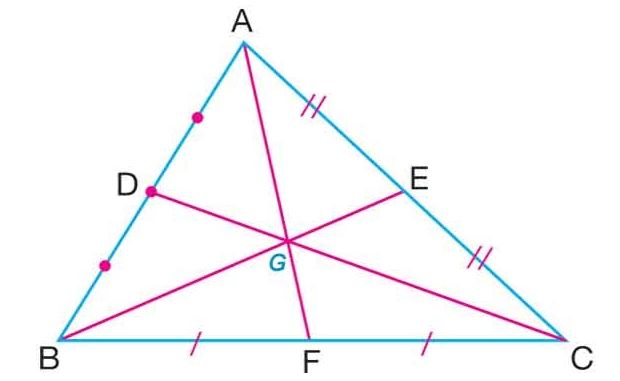
Burada [AF] kenarortayı, BC kenarını iki eşit parçaya böler.
📌 Önemli Bilgi: Ağırlık merkezi, üçgenin dengede durduğu noktadır.
📌 Bu konuda öğrendiklerimiz:
✅ Üçgenin temel bileşenlerini öğrendik.
✅ Yüksekliğin nasıl çizildiğini inceledik.
✅ Açıortay ve kenarortay kavramlarını öğrendik.
✅ Üçgenin özel noktaları hakkında bilgi edindik.
Üçgenin İç Açılar ve Dış Açılar Toplamı
Üçgenlerin en önemli özelliklerinden biri iç açıları ve dış açıları arasındaki ilişkilerdir. Bu kurallar, geometri problemlerini çözmede büyük kolaylık sağlar.
Bu bölümde, üçgenin iç açılar toplamı, dış açılar toplamı ve iç-dış açı ilişkilerini öğreneceğiz. 🚀
1. Üçgenin İç Açılar Toplamı
📌 Kural:
Bir üçgenin iç açılarının toplamı her zaman 180°’dir.
✔ A, B ve C iç açıları olan bir üçgen için:

Eğer ∠A = 60° ve ∠B = 70° ise, ∠C kaç derecedir?
✔ Çözüm:

✅ Cevap: ∠C = 50°
📌 Önemli Bilgi: Bir üçgende iki açıyı biliyorsak, üçüncüsünü kolayca bulabiliriz.
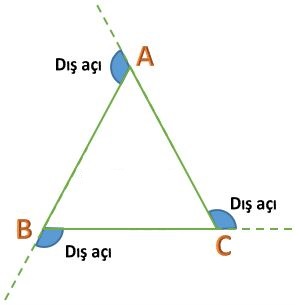
2. Üçgenin Dış Açılar Toplamı
📌 Kural:
Bir üçgenin dış açılarının toplamı her zaman 360°’dir.
✔ Dış açı, iç açının uzantısıdır.
✔ Bir üçgenin her köşesindeki dış açılar bulunarak toplam 360° olduğu gösterilebilir.
✅ Örnek:
3. Bir Dış Açının Karşısındaki İki İç Açı ile İlişkisi
📌 Kural:
Bir üçgenin herhangi bir dış açısı, kendisine komşu olmayan iki iç açının toplamına eşittir.
✔ Örnek:
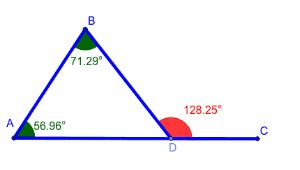
✔ Burada ∠D dış açısı için:
![]()
✅ Örnek:
Eğer ∠A = 50° ve ∠B = 60° ise, ∠D kaçtır?
✔ Çözüm:
✅ Cevap: ∠D = 110°
📌 Sonuç: Bir dış açıyı bulmak için, iki iç açıyı toplayabiliriz.
4. Özel Üçgenlerde İç ve Dış Açılar
✔ Eşkenar Üçgen:
- Her iç açı 60°’dir.
- Her dış açı 120°’dir.
✔ İkizkenar Üçgen:
- İki iç açı birbirine eşittir.
- Dış açılar da birbirine eşittir.
✔ Dik Üçgen:
- Bir açısı 90° olduğu için diğer iki iç açının toplamı 90°’dir.
✅ Örnek:
Bir dik üçgende, bir açı 30° ise diğer açı kaçtır?
✔ Çözüm:
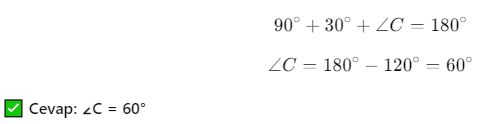
📌 Bu konuda öğrendiklerimiz:
✅ Üçgenin iç açılar toplamının 180° olduğunu öğrendik.
✅ Üçgenin dış açılar toplamının 360° olduğunu inceledik.
✅ Bir dış açının karşısındaki iki iç açının toplamına eşit olduğunu öğrendik.
✅ Özel üçgenlerde iç ve dış açı ilişkilerini öğrendik.
Üçgenin Kenar Uzunlukları ve Üçgen Eşitsizliği
Bir üçgenin kenar uzunlukları belirli kurallara uymak zorundadır. Herhangi üç uzunluk rastgele bir araya gelerek üçgen oluşturamaz. Üçgen eşitsizliği, bir üçgenin oluşabilmesi için kenar uzunlukları arasındaki ilişkiyi belirler.
Bu bölümde, üçgenin kenar uzunlukları ile ilgili temel kuralları ve üçgen eşitsizliği kuralını inceleyeceğiz. 🚀
1. Üçgenin Kenar Uzunlukları Arasındaki İlişki
📌 Kural:
Bir üçgende herhangi iki kenarın toplamı, üçüncü kenardan büyük olmalıdır.
✔ Matematiksel gösterimi:
Eğer üçgenin kenar uzunlukları a, b ve c ise:

📌 Örnek:
Aşağıdaki kenarlar bir üçgen oluşturur mu?
- a = 5 cm, b = 7 cm, c = 10 cm
✔ Koşulları kontrol edelim:
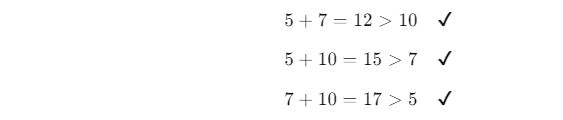
✅ Sonuç: Bu üç kenar uzunluğu bir üçgen oluşturur.
2. Üçgen Eşitsizliği
📌 Tanım:
Üçgen eşitsizliği, üçgenin herhangi bir iki kenarının toplamının üçüncü kenardan büyük olması gerektiğini belirtir.
✅ Örnek:
Aşağıdaki kenarlar bir üçgen oluşturabilir mi?
- a = 3 cm, b = 4 cm, c = 8 cm
✔ Kontrol edelim:
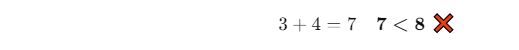
✅ Sonuç: Bu üç kenar uzunluğu bir üçgen oluşturamaz.
📌 Önemli Bilgi: Eğer herhangi iki kenarın toplamı üçüncü kenardan küçük veya eşitse, üçgen oluşmaz.
3. Üçgen Çeşitleri ve Kenar Uzunlukları
Üçgenler kenar uzunluklarına göre 3 gruba ayrılır:
✔ Eşkenar Üçgen:
- Tüm kenar uzunlukları birbirine eşittir.
- Örnek: a = b = c
✔ İkizkenar Üçgen:
- İki kenar uzunluğu eşittir.
- Örnek: a = b, c farklıdır.
✔ Çeşitkenar Üçgen:
- Tüm kenar uzunlukları farklıdır.
- Örnek: a ≠ b ≠ c
✅ Örnek:
Bir üçgenin kenarları 5 cm, 5 cm ve 8 cm ise, bu üçgenin türü nedir?
✔ Çözüm:
- İki kenar eşit olduğuna göre, bu bir ikizkenar üçgendir.
✅ Cevap: İkizkenar üçgen.
4. Özel Üçgenler ve Kenar Uzunlukları
Bazı üçgenler özel oranlara sahiptir:
✔ Dik Üçgen (Pisagor Üçgeni):
- Özel üçgenlerden bazıları:
- 3 – 4 – 5
- 5 – 12 – 13
- 7 – 24 – 25
✔ Eşkenar Üçgen:
- Tüm kenarları eşit olduğu için yükseklik formülü:

✔ Altın Üçgen:
- Kenar uzunlukları altın oran (1.618) ile ilişkilidir.
✅ Örnek:
Bir üçgenin kenarları 3, 4 ve 5 ise, bu hangi özel üçgendir?
✔ Pisagor bağıntısını kontrol edelim:
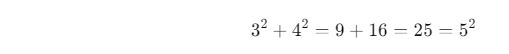
✅ Cevap: Bu, bir 3-4-5 özel dik üçgenidir.
📌 Bu konuda öğrendiklerimiz:
✅ Üçgenin kenar uzunlukları arasındaki ilişkiyi öğrendik.
✅ Üçgen eşitsizliği kuralını inceledik.
✅ Üçgenlerin kenar uzunluklarına göre çeşitlerini öğrendik.
✅ Özel üçgenleri ve kenar uzunluklarını öğrendik.
Üçgen Çeşitleri (Kenarlarına ve Açılarının Ölçüsüne Göre)
Üçgenler, kenar uzunluklarına ve açı ölçülerine göre sınıflandırılır. Bu sınıflandırmalar, üçgenin şekli ve açıları hakkında önemli bilgiler verir.
1. Kenar Uzunluklarına Göre Üçgenler
Bir üçgen, kenarlarının uzunluklarına göre üç farklı kategoriye ayrılır:
✔ Eşkenar Üçgen
✔ İkizkenar Üçgen
✔ Çeşitkenar Üçgen
A) Eşkenar Üçgen
📌 Tanım:
Üç kenarı da eşit olan üçgendir.
✔ Bütün iç açıları 60°’dir.
✔ Simetriğe sahiptir ve tüm açıortaylar, kenarortaylar ve yükseklikler eşittir.
✅ Örnek:
Bir eşkenar üçgenin bir kenarı 6 cm ise, diğer kenarlar da 6 cm’dir.
📌 Özel Bilgi: Eşkenar üçgenin yüksekliği şu formülle bulunur:

B) İkizkenar Üçgen
📌 Tanım:
İki kenarı eşit olan üçgendir.
✔ Eşit kenarların karşısındaki açılar da eşittir.
✔ Üçüncü kenara “taban”, eşit kenarlara “yan kenar” denir.
✅ Örnek:
Bir üçgenin iki kenarı 7 cm, üçüncü kenarı 5 cm ise bu bir ikizkenar üçgendir.
📌 Özel Bilgi: İkizkenar üçgende yükseklik aynı zamanda açıortay ve kenarortaydır.
C) Çeşitkenar Üçgen
📌 Tanım:
Üç kenarı da farklı uzunlukta olan üçgendir.
✔ Tüm açılar farklıdır.
✔ Simetriye sahip değildir.
✅ Örnek:
Bir üçgenin kenarları 5 cm, 7 cm ve 9 cm ise bu bir çeşitkenar üçgendir.
📌 Özel Bilgi: Çeşitkenar üçgenlerde yükseklikler, kenarortaylar ve açıortaylar birbirinden farklıdır.
2. Açılarına Göre Üçgenler
Bir üçgen, açı ölçülerine göre üç farklı kategoriye ayrılır:
✔ Dar Açılı Üçgen
✔ Dik Açılı Üçgen
✔ Geniş Açılı Üçgen
A) Dar Açılı Üçgen
📌 Tanım:
Tüm açıları 90°’den küçük olan üçgendir.
✔ Her iç açısı 90°’den küçüktür.
✔ En sık rastlanan üçgen türlerinden biridir.
✅ Örnek:
Bir üçgenin açıları 50°, 60° ve 70° ise bu bir dar açılı üçgendir.
B) Dik Açılı Üçgen
📌 Tanım:
Bir açısı tam olarak 90° olan üçgendir.
✔ Dik açı oluşturan kenarlara “dik kenarlar”, karşısındaki kenara “hipotenüs” denir.
✔ Pisagor Teoremi bu üçgende kullanılır:
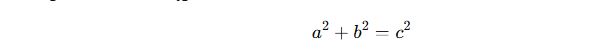
✅ Örnek:
Bir üçgenin açıları 30°, 60° ve 90° ise bu bir dik üçgendir.
📌 Özel Bilgi: Özel Pisagor üçgenleri vardır (3-4-5, 5-12-13 vb.).
C) Geniş Açılı Üçgen
📌 Tanım:
Bir açısı 90°’den büyük olan üçgendir.
✔ Geniş açının karşısındaki kenar en uzundur.
✔ Geniş açı içeren üçgenlerde Pisagor Teoremi yerine kosinüs teoremi kullanılır.
✅ Örnek:
Bir üçgenin açıları 40°, 30° ve 110° ise bu bir geniş açılı üçgendir.
3. Özel Üçgenler
✔ Eşkenar Üçgen → Her açısı 60°’dir.
✔ İkizkenar Dik Üçgen → Açıları 45°-45°-90° olan dik üçgendir.
✔ 30°-60°-90° Üçgeni → Özel bir dik üçgendir.
✅ Örnek:
Bir üçgenin açıları 30°, 60° ve 90° ise bu özel bir dik üçgendir.
📌 Önemli Bilgi: Özel üçgenlerin kenar uzunlukları belirli oranlarla bulunur.
📌 Bu konuda öğrendiklerimiz:
✅ Üçgenleri kenar uzunluklarına göre sınıflandırdık.
✅ Üçgenleri açılarına göre sınıflandırdık.
✅ Özel üçgenleri ve özelliklerini inceledik.
Pisagor Teoremi
📌 Tanım:
Pisagor Teoremi, dik üçgenlerde hipotenüs ve dik kenarlar arasındaki ilişkiyi açıklayan temel bir matematiksel kuraldır.
✔ Dik üçgende hipotenüs, dik açı karşısındaki en uzun kenardır.
✔ Pisagor bağıntısı şu şekilde ifade edilir:

Burada:
- a ve b → Dik kenarlar
- c → Hipotenüs (en uzun kenar)
🚀 Bu teorem, dik üçgen problemlerini çözerken büyük kolaylık sağlar.
1. Pisagor Teoremi ile Hipotenüs Bulma
📌 Örnek:
Bir dik üçgende dik kenarlar 3 cm ve 4 cm ise, hipotenüs uzunluğu kaç cm’dir?
✔ Pisagor formülünü uygulayalım:
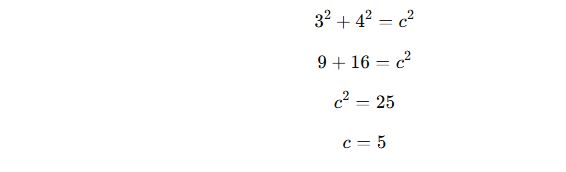
✅ Cevap: Hipotenüs 5 cm’dir.
📌 Özel Bilgi: Bu, en bilinen özel Pisagor üçgenlerinden biridir (3-4-5 üçgeni).
2. Pisagor Teoremi ile Dik Kenar Bulma
📌 Örnek:
Hipotenüsü 13 cm, bir dik kenarı 5 cm olan dik üçgenin diğer dik kenarını bulun.
✔ Pisagor formülünü uygulayalım:
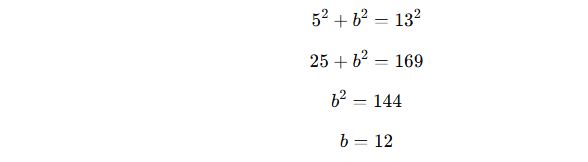
✅ Cevap: Diğer dik kenar 12 cm’dir.
📌 Özel Bilgi: Bu, 5-12-13 özel Pisagor üçgenidir.
3. Özel Pisagor Üçgenleri
Bazı üçgenler Pisagor bağıntısını doğal sayılarla sağlar. En yaygın özel üçgenler şunlardır:
✔ 3 – 4 – 5
✔ 5 – 12 – 13
✔ 7 – 24 – 25
✔ 8 – 15 – 17
📌 Örnek:
Bir dik üçgenin bir kenarı 8 cm ve hipotenüsü 17 cm ise, diğer kenarı nedir?
✔ Pisagor Teoremini uygulayalım:
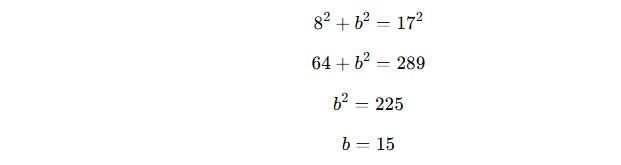
✅ Cevap: Diğer kenar 15 cm’dir.
📌 Bu, 8-15-17 özel Pisagor üçgenidir.
4. Pisagor Teoreminin Günlük Hayattaki Kullanımı
✔ Haritacılık ve Navigasyon: İki nokta arasındaki en kısa mesafe hesaplanır.
✔ İnşaat ve Mimarlık: Bina, köprü ve çatı yapılarında kullanılır.
✔ Bilgisayar Grafikleri: Oyun ve animasyonlarda karakterlerin mesafeleri hesaplanır.
✅ Örnek:
Bir bina 12 m yüksekliğinde ve yerden 5 m uzaktaki bir noktaya merdiven dayandığında, merdivenin uzunluğu nedir?
✔ Pisagor Teoremini uygulayalım:
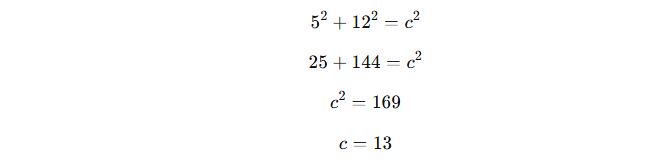
✅ Cevap: Merdivenin uzunluğu 13 m’dir.
📌 Bu konuda öğrendiklerimiz:
✅ Pisagor Teoremini öğrendik ve nasıl uygulanacağını inceledik.
✅ Hipotenüs ve dik kenar bulma yöntemlerini öğrendik.
✅ Özel Pisagor üçgenlerini tanıdık.
✅ Günlük hayatta Pisagor Teoreminin kullanım alanlarını gördük.
Özel Üçgenler (3-4-5, 5-12-13 vb.)
Özel üçgenler, kenar uzunlukları belirli oranlarda olan ve Pisagor Teoremi’ni sağlayan üçgenlerdir. Bu üçgenler, geometri problemlerini çözerken büyük kolaylık sağlar çünkü uzunluklar arasında önceden belirlenmiş bir ilişki vardır.
1. 3-4-5 Üçgeni
📌 Tanım:
Bu üçgenin kenar uzunlukları 3, 4 ve 5 birim olup, Pisagor Teoremi’ni sağlar:
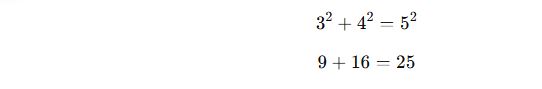
✅ Özellikler:
✔ Dik üçgendir.
✔ Dik kenarlar 3 ve 4 birimdir, hipotenüs 5 birimdir.
✔ Bu üçgenin katları da (örneğin 6-8-10, 9-12-15) özel üçgen oluşturur.
✅ Örnek:
Bir üçgenin kenarları 6 cm, 8 cm ve 10 cm ise bu bir özel 3-4-5 üçgeninin 2 katıdır.
📌 Sonuç: Bu üçgen dik üçgendir ve hesaplamalarda zaman kazandırır.
2. 5-12-13 Üçgeni
📌 Tanım:
Bu üçgenin kenar uzunlukları 5, 12 ve 13 birimdir ve Pisagor Teoremi’ni sağlar:
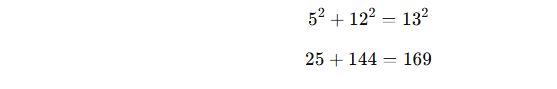
✅ Özellikler:
✔ Dik üçgendir.
✔ Dik kenarlar 5 ve 12 birimdir, hipotenüs 13 birimdir.
✔ Bu üçgenin katları da (örneğin 10-24-26) özel üçgen oluşturur.
✅ Örnek:
Bir dik üçgende dik kenarlardan biri 10 cm, hipotenüs 26 cm ise diğer kenar 24 cm’dir (5-12-13 üçgeninin 2 katıdır).
📌 Sonuç: Bu üçgen, dik üçgenlerde uzunlukları hızlı bulmada kullanılır.
3. 7-24-25 Üçgeni
📌 Tanım:
Bu üçgenin kenar uzunlukları 7, 24 ve 25 birimdir ve Pisagor Teoremi’ni sağlar:
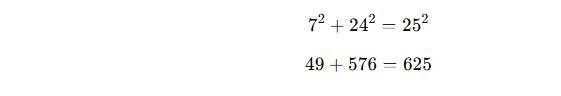
✅ Özellikler:
✔ Dik üçgendir.
✔ Dik kenarlar 7 ve 24 birimdir, hipotenüs 25 birimdir.
✅ Örnek:
Eğer dik kenarlardan biri 14 cm, hipotenüs 50 cm ise diğer dik kenar 48 cm’dir (7-24-25 üçgeninin 2 katıdır).
📌 Sonuç: Bu üçgen büyük kenarlarla çalışırken kullanışlıdır.
4. 8-15-17 Üçgeni
📌 Tanım:
Bu üçgenin kenar uzunlukları 8, 15 ve 17 birimdir ve Pisagor Teoremi’ni sağlar:
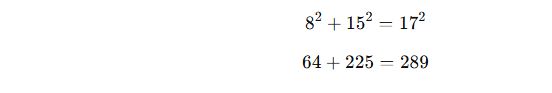
✅ Özellikler:
✔ Dik üçgendir.
✔ Dik kenarlar 8 ve 15 birimdir, hipotenüs 17 birimdir.
✅ Örnek:
Eğer dik kenarlardan biri 16 cm, hipotenüs 34 cm ise diğer dik kenar 30 cm’dir (8-15-17 üçgeninin 2 katıdır).
📌 Sonuç: Bu üçgen, diğer özel üçgenler gibi hesaplamalarda büyük kolaylık sağlar.
5. Özel Üçgenlerin Kullanımı
✔ İnşaat ve Mimarlık:
- Duvar, merdiven ve köprü hesaplamalarında özel üçgenler kullanılır.
✔ Haritacılık ve Navigasyon:
- İki nokta arasındaki en kısa mesafeyi hesaplamak için kullanılır.
✔ Mühendislik ve Fizik:
- Kuvvet hesaplamaları ve eğim açılarında bu üçgenler kullanılır.
📌 Bu konuda öğrendiklerimiz:
✅ Özel üçgenleri tanıdık.
✅ 3-4-5, 5-12-13, 7-24-25 ve 8-15-17 üçgenlerinin özelliklerini öğrendik.
✅ Bu özel üçgenlerin günlük hayatta nasıl kullanıldığını gördük.
Üçgenler Konu Özeti
Bu konu boyunca üçgenlerin temel özelliklerini, çeşitlerini, kenar ve açı kurallarını, Pisagor Teoremi’ni ve özel üçgenleri öğrendik. İşte öğrendiklerimizin kısa bir özeti:
1. Üçgenin Temel Elemanları
📌 Üçgenin temel bileşenleri:
✔ Kenarlar: Üçgeni oluşturan doğrular (AB, BC, CA)
✔ Köşeler: İki kenarın birleştiği noktalar (A, B, C)
✔ Açılar: İç açıların toplamı 180°’dir
📌 Özel bileşenler:
✔ Yükseklik: Bir köşeden karşı kenara inen dik doğru parçası
✔ Açıortay: Bir açıyı iki eş parçaya bölen doğru
✔ Kenarortay: Bir köşeden karşı kenarın orta noktasına çizilen doğru
2. Üçgenin Açılar ve Kenarlarla İlgili Temel Kuralları

3. Üçgenin Kenar Uzunlukları ve Üçgen Eşitsizliği
📌 Üçgen oluşturma şartı:
Herhangi iki kenarın toplamı üçüncü kenardan büyük olmalıdır.
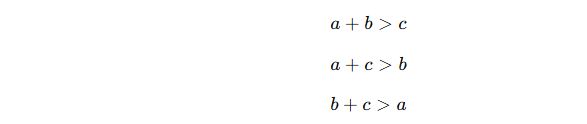
✅ Örnek:
Bir üçgenin kenarları 5 cm, 7 cm ve 10 cm ise:
✔ 5 + 7 = 12 > 10 ✅
✔ 5 + 10 = 15 > 7 ✅
✔ 7 + 10 = 17 > 5 ✅
Bu üçgen oluşabilir.
4. Üçgen Çeşitleri
📌 Kenar uzunluklarına göre üçgenler:
✔ Eşkenar Üçgen: Üç kenar eşit, her açı 60°
✔ İkizkenar Üçgen: İki kenar eşit, eşit kenarların karşısındaki açılar da eşit
✔ Çeşitkenar Üçgen: Tüm kenar uzunlukları farklı
📌 Açılarına göre üçgenler:
✔ Dar Açılı Üçgen: Tüm açılar 90°’den küçük
✔ Dik Açılı Üçgen: Bir açı 90°
✔ Geniş Açılı Üçgen: Bir açı 90°’den büyük
5. Pisagor Teoremi ve Özel Üçgenler
📌 Pisagor Teoremi (Dik Üçgenler için):

✔ a ve b: Dik kenarlar
✔ c: Hipotenüs
📌 Özel üçgenler:
✔ 3-4-5 üçgeni
✔ 5-12-13 üçgeni
✔ 7-24-25 üçgeni
✔ 8-15-17 üçgeni
✅ Örnek:
Bir dik üçgenin dik kenarları 6 cm ve 8 cm ise hipotenüs:

📌 Bu konu kapsamında öğrendiklerimiz:
✅ Üçgenin temel elemanlarını tanıdık.
✅ Üçgenin iç açılar ve dış açılar toplamını inceledik.
✅ Üçgen eşitsizliği ile üçgen oluşturma kurallarını öğrendik.
✅ Üçgenleri kenar uzunluklarına ve açılarına göre sınıflandırdık.
✅ Pisagor Teoremi’ni ve özel üçgenleri öğrendik.
8. Sınıf Matematik Üçgenler Çözümlü Örnek Sorular
1. Üçgenin İç Açılar Toplamı
📌 Soru 1:
Bir üçgenin iç açılarından ikisi 45° ve 65° ise, üçüncü açı kaç derecedir?

2. Üçgen Eşitsizliği
📌 Soru 2:
Bir üçgenin iki kenar uzunluğu 5 cm ve 8 cm. Üçüncü kenar uzunluğu en az kaç cm ve en fazla kaç cm olabilir?

3. Dik Üçgen ve Pisagor Teoremi
📌 Soru 3:
Bir dik üçgende, dik kenarlar 6 cm ve 8 cm. Hipotenüs uzunluğu kaç cm’dir?

4. Dış Açı Kuralı
📌 Soru 4:
Bir üçgenin iki iç açısı 40° ve 55°. Bu üçgenin bu iki açının dışındaki üçüncü açısına komşu olan dış açı kaç derecedir?

5. Kenar Uzunlukları Verilen Üçgenin Türü
📌 Soru 5:
Bir üçgenin kenar uzunlukları 7 cm, 7 cm ve 10 cm. Bu üçgenin türü nedir?
Çözüm:
✔ İki kenar uzunluğu eşit olduğuna göre, bu bir “ikizkenar üçgen”dir.
✅ Cevap: İkizkenar üçgen.
6. Üçgenin Açılarına Göre Türü
📌 Soru 6:
Bir üçgenin iç açıları 35°, 55° ve 90°. Bu üçgenin türü nedir?
Çözüm:
✔ Bir açısı 90° olduğuna göre, bu bir dik üçgendir.
✅ Cevap: Dik Üçgen.
7. Özel Üçgen (3-4-5 Üçgeni)
📌 Soru 7:
Bir dik üçgenin dik kenarlarından biri 9 cm, hipotenüsü 15 cm. Diğer dik kenar uzunluğu kaç cm’dir?

8. İkizkenar Üçgende Yükseklik
📌 Soru 8:
Bir ikizkenar üçgende eşit kenarlar 10 cm, taban 12 cm. Bu üçgende tabana ait yükseklik kaç cm’dir?

9. Üçgenin Kenar Uzunlukları ile Eşitsizlik Kurma
📌 Soru 9:
Bir üçgenin kenarlarından ikisi 9 cm ve 14 cm. Üçüncü kenarın uzunluğu hangi değerler arasında olabilir?

10. Eşkenar Üçgenin Yüksekliği
📌 Soru 10:
Bir eşkenar üçgenin bir kenarı 10 cm. Bu üçgenin yüksekliği kaç cm’dir?

📌 Bu 10 soru ile şunları öğrendik:
✔ Üçgenin iç açılar toplamı ve dış açı kurallarını kullandık.
✔ Üçgen eşitsizliği kurallarını uyguladık.
✔ Pisagor Teoremi ile hipotenüs ve dik kenar hesapladık.
✔ Özel üçgenleri ve eşkenar üçgen yükseklik hesaplamalarını öğrendik.
✔ Üçgen çeşitlerini açılarına ve kenarlarına göre belirledik.

