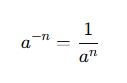Matematikte bazı işlemleri daha pratik ve kısa bir şekilde ifade etmek için üslü ifadeler kullanılır. Üslü ifadeler, bir sayının kendisiyle tekrar eden çarpımlarını göstermek için kullanılır. Örneğin, 2 × 2 × 2 × 2 işlemini yazmak yerine 2⁴ şeklinde göstererek hem yazımı kolaylaştırırız hem de daha düzenli bir ifade elde ederiz.

Üslü ifadeler, matematiğin birçok alanında kullanıldığı gibi bilimsel hesaplamalar, büyük ve küçük sayılarla işlem yapma, fizik ve mühendislik problemleri gibi alanlarda da sıkça karşımıza çıkar. Bu konu kapsamında öncelikle tam sayıların üslü ifadeleri, ardından üslü ifadelerde temel kurallar, ondalık gösterimleri çözümleme, sayıları 10’un kuvvetleri ile ifade etme ve bilimsel gösterim konularını detaylıca inceleyeceğiz.

8. Sınıf Matematik Üslü İfadeler Konu Anlatımı

Tam Sayıların Tam Sayı Kuvvetleri

Matematikte bazı işlemleri daha kısa ve pratik hale getirmek için üslü ifadeler kullanılır. Tam sayıların tam sayı kuvvetleri, bir tam sayının kendisiyle kaç defa çarpıldığını gösteren özel bir yazım biçimidir. Bu konuyu iyi anlamak, matematikte birçok işlemde hız kazanmamıza yardımcı olur. Şimdi üslü ifadelerin tanımıyla başlayalım.

1. Üslü İfadelerin Tanımı

Bir sayının kendisiyle tekrar eden çarpımını üslü ifade olarak yazarız.

📌 Üslü bir ifade, aⁿ şeklinde gösterilir ve şu şekilde okunur:

• a: Taban (tekrar eden sayı)
• n: Üs (kaç kez çarpıldığını gösterir)

✅ Örnekler:

• 2³ = 2 × 2 × 2 = 8
• 5² = 5 × 5 = 25
• (-3)⁴ = (-3) × (-3) × (-3) × (-3) = 81

2. Üslü İfadelerin Özellikleri

a) Pozitif Üsler

Bir sayının üssü pozitif bir tam sayı olduğunda, o sayı kendisiyle üs kadar çarpılır.

✅ Örnekler:

• 3⁴ = 3 × 3 × 3 × 3 = 81
• (-2)³ = (-2) × (-2) × (-2) = -8

📌 Not:

• Negatif sayılar parantez içinde üslü olarak yazıldığında, üssü çift ise sonuç pozitif, tek ise sonuç negatif olur.
  • (-2)² = (-2) × (-2) = 4 ✅
  • (-2)³ = (-2) × (-2) × (-2) = -8 ❌

b) Üssü 1 Olan Sayılar

Herhangi bir sayının üssü 1 olduğunda, sonuç o sayının kendisidir:
✅ Örnekler:

• 7¹ = 7
• (-5)¹ = -5

c) Üssü 0 Olan Sayılar

Bir sayının üssü 0 olduğunda, sonuç daima 1’dir.

✅ Örnekler:

• 4⁰ = 1
• (-7)⁰ = 1
• 125⁰ = 1

📌 İstisna:

• 0⁰ belirsiz bir ifadedir ve özel durumlarda değerlendirilir.

3. Negatif Üs Kavramı

Üs negatif olduğunda, üslü sayı kesirli bir ifadeye dönüşür.

📌 Kural:
a−n=1ana^{-n} = \frac{1}{a^n}a−n=an1​

✅ Örnekler:

• 2⁻³ = 1 / (2³) = 1 / 8
• 5⁻² = 1 / (5²) = 1 / 25
• (-3)⁻² = 1 / ((-3)²) = 1 / 9

4. Üslü İfadelerde İşlem Önceliği

Matematikte üslü ifadeler içeren işlemleri yaparken işlem sırasına dikkat etmek gerekir:

1. Parantez içindeki işlemler yapılır.
2. Üslü işlemler hesaplanır.
3. Çarpma, bölme, toplama ve çıkarma işlemleri yapılır.

✅ Örnek:
2 + 3² × 4 = ?

1. Üs hesaplanır: 3² = 9
2. Çarpma yapılır: 9 × 4 = 36
3. Toplama yapılır: 2 + 36 = 38

✅ Cevap: 38

5. Üslü İfadelerde İşlem Kuralları

Üslü ifadelerle işlem yaparken bazı temel kurallar vardır. Bunlar ilerleyen konularda detaylıca ele alınacaktır, ancak burada temel bir giriş yapalım.

a) Çarpma Kuralı (Tabanlar Aynıysa Üsler Toplanır)

am×an=am+na^m \times a^n = a^{m+n}am×an=am+n

✅ Örnek:

• 2³ × 2² = 2⁵ = 32
• 5⁴ × 5³ = 5⁷

b) Bölme Kuralı (Tabanlar Aynıysa Üsler Çıkarılır)

aman=am−n\frac{a^m}{a^n} = a^{m-n}anam​=am−n

✅ Örnek:

• 8⁵ ÷ 8³ = 8² = 64
• 10⁷ ÷ 10² = 10⁵

c) Üstün Üste Olması (Üslerin Çarpılması)

(am)n=am×n(a^m)^n = a^{m \times n}(am)n=am×n

✅ Örnek:

• (2³)² = 2⁶ = 64
• (5²)³ = 5⁶

📌 Bu konuda öğrendiklerimiz:
✅ Üslü ifadelerin ne olduğunu ve nasıl yazıldığını öğrendik.
✅ Pozitif, negatif ve sıfır üslü sayıların özelliklerini inceledik.
✅ Üslü ifadelerin işlem önceliği ve kuralları hakkında giriş yaptık.

Üslü İfadelerde Temel Kurallar (İşlemler)

Üslü ifadelerle işlemler yaparken bazı temel kurallar vardır. Bu kurallar sayesinde üslü ifadelerle daha kolay ve hızlı işlem yapabiliriz. Şimdi çarpma, bölme, üs alma ve diğer kuralları detaylı bir şekilde inceleyelim.

1. Üslü Sayılarla Çarpma Kuralı

Tabanları aynı olan üslü sayılar çarpılırken üsler toplanır.

📌 Kural:

✅ Örnekler:

• 2³ × 2² = 2⁵ = 32
• 5⁴ × 5² = 5⁶ = 15,625
• (3²) × (3⁵) = 3⁷ = 2,187

📌 Özel Durum:

• Farklı tabanlarda çarpma yapılırken, üsler toplanmaz!
  • Örnek: 2³ × 3² ≠ 6⁵ (Ayrı ayrı hesaplanmalıdır: 8 × 9 = 72)

2. Üslü Sayılarla Bölme Kuralı

Tabanları aynı olan üslü sayılar bölünürken üsler çıkarılır.

📌 Kural:

✅ Örnekler:

• 8⁵ ÷ 8³ = 8² = 64
• 10⁷ ÷ 10² = 10⁵ = 100,000
• (4⁶) ÷ (4²) = 4⁴ = 256

📌 Özel Durum:

• Farklı tabanlarda bölme yapılırken, üsler çıkarılmaz!
  • Örnek: 6³ ÷ 3² ≠ 2¹

3. Üstün Üste Olması (Üstün Üste Üs Alma Kuralı)

Bir üslü sayı tekrar üslü hale getirilirse üsler çarpılır.

📌 Kural:

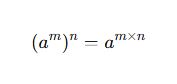
✅ Örnekler:

• (2³)² = 2⁶ = 64
• (5²)³ = 5⁶ = 15,625
• (3⁴)² = 3⁸ = 6,561

📌 Özel Durum:

• (a × b)^m = a^m × b^m kuralı da kullanılabilir.
  • Örnek: (2 × 3)⁴ = 2⁴ × 3⁴ = 16 × 81 = 1296

4. Üssü 0 Olan Sayılar

Bir sayının üssü 0 olduğunda, sonuç daima 1 olur.

📌 Kural:

✅ Örnekler:

• 4⁰ = 1
• (-7)⁰ = 1
• 125⁰ = 1

📌 Özel Durum:

• 0⁰ belirsiz bir ifadedir!

5. Negatif Üs Kuralı

Negatif üs, sayının tersini almak anlamına gelir.

📌 Kural:

​

✅ Örnekler:

• 2⁻³ = 1 / (2³) = 1 / 8
• 5⁻² = 1 / (5²) = 1 / 25
• (-3)⁻² = 1 / ((-3)²) = 1 / 9

📌 Özel Durum:

• Taban negatifse, üs çift olduğunda sonuç pozitif, tek olduğunda negatif olur.
  • Örnek: (-2)⁻³ = -1 / 8

6. Üslü Sayılarla Toplama ve Çıkarma İşlemleri

Üslü ifadeler sadece taban ve üs aynıysa toplanabilir veya çıkarılabilir.

📌 Örnekler:
✔ 2³ + 2³ = 8 + 8 = 16
✔ 3⁵ – 3⁵ = 243 – 243 = 0
✖ 2² + 3² ≠ 5² (Yanlış!)

✅ Özel Durum:
Üslü ifadeler ortak çarpan parantezine alınabilir:

• 2³ + 2² = 2² (2 + 1) = 4 × 3 = 12

7. Üslü Sayılarla Karışık İşlemler

Üslü ifadelerle işlem yaparken öncelik sırası şudur:

1. Parantez içindeki işlemler yapılır.
2. Üslü işlemler hesaplanır.
3. Çarpma ve bölme yapılır.
4. Toplama ve çıkarma yapılır.

✅ Örnek:
📌 (2² + 3³) ÷ 3 = ?

1. 2² = 4 ve 3³ = 27
2. (4 + 27) = 31
3. 31 ÷ 3 = 10.33

✅ Cevap: 10.33

📌 Bu konuda öğrendiklerimiz:
✅ Üslü ifadelerle çarpma, bölme ve üs alma kurallarını öğrendik.
✅ 0 ve negatif üs kavramlarını inceledik.
✅ Üslü ifadelerde işlem önceliğini anladık.

Ondalık Gösterimleri Çözümleme

Ondalık gösterimleri çözümlemek, sayıları basamak değerlerine ayırarak incelememizi sağlar. Üslü ifadeler ile ondalık sayılar arasındaki ilişkiyi kurarak bilimsel gösterim, büyük ve küçük sayıların üslü ifadelerle yazımı gibi konulara temel oluşturur. Şimdi bu konuyu detaylı bir şekilde ele alalım.

1. Ondalık Sayıların Çözümlemesi

Bir ondalık sayı, tam kısmı ve ondalık kısmı olmak üzere iki bölümden oluşur:

📌 Örnek: 358,72 sayısını ele alalım:

• Tam kısım: 358
• Ondalık kısım: 0,72

Bu sayıyı basamaklarına ayırarak yazalım:

✅ Çözümleme:

• 3 × 10² → 3 tane 100
• 5 × 10¹ → 5 tane 10
• 8 × 10⁰ → 8 tane 1
• 7 × 10⁻¹ → 7 tane 0.1
• 2 × 10⁻² → 2 tane 0.01

📌 Sonuç: 358,72 = (3 × 100) + (5 × 10) + (8 × 1) + (7 × 0.1) + (2 × 0.01)

Bu şekilde her sayıyı 10’un kuvvetleri ile çözümleyebiliriz.

2. Ondalık Kesirleri Üslü İfadelerle Yazma

Ondalık kesirleri 10’un negatif kuvvetleri ile yazabiliriz.

📌 Örnekler:

• 0,1 = 10⁻¹
• 0,01 = 10⁻²
• 0,001 = 10⁻³
• 0,0001 = 10⁻⁴

✅ Örnek:
0,045 sayısını üslü ifadeyle yazalım.

Bu gösterim, bilimsel gösterim için temel oluşturur.

3. Tam Sayılar ve Ondalık Sayılar Arasında Bağlantı

Tam sayılar pozitif üslü ifadelerle, ondalık kesirler ise negatif üslü ifadelerle gösterilir.

📌 Örnek:

• 100 = 10²
• 10 = 10¹
• 1 = 10⁰
• 0,1 = 10⁻¹
• 0,01 = 10⁻²
• 0,001 = 10⁻³

Bu düzen sayesinde büyük ve küçük sayıları kolayca yazabiliriz.

4. Sayıları 10’un Kuvvetleri ile Gösterme

10’un kuvvetlerini kullanarak çok büyük ve çok küçük sayıları kısa bir şekilde yazabiliriz.

📌 Örnekler:

• 10 = 10¹
• 100 = 10²
• 1.000 = 10³
• 10.000 = 10⁴

Aynı şekilde küçük sayılar:

• 0,1 = 10⁻¹
• 0,01 = 10⁻²
• 0,001 = 10⁻³

✅ Örnek:
500.000 sayısını 10’un kuvvetiyle gösterelim.

✅ Örnek:
0,00032 sayısını 10’un kuvvetiyle yazalım.

Bu yöntem, bilimsel gösterimin temelidir.

📌 Bu konuda öğrendiklerimiz:
✅ Ondalık sayıları basamaklarına ayırarak çözümledik.
✅ Ondalık kesirleri üslü ifadelerle nasıl yazacağımızı öğrendik.
✅ Sayıları 10’un kuvvetleri ile ifade ettik.

Sayıları 10’un Tam Sayı Kuvvetleri ile İfade Etme

Matematikte bazı büyük veya küçük sayıları yazmak ve işlem yapmak bazen zor olabilir. Bu tür sayıları 10’un tam sayı kuvvetleriyle ifade etmek, işlemleri daha kolay hale getirir. Şimdi bu yöntemi detaylıca inceleyelim.

1. 10’un Kuvvetleri Nedir?

10’un kuvvetleri, 10’un kendisiyle tekrar eden çarpımları veya bölümleri olarak tanımlanır.

📌 Pozitif Üsler (Büyük Sayılar)

• 10¹ = 10
• 10² = 10 × 10 = 100
• 10³ = 10 × 10 × 10 = 1.000
• 10⁴ = 10 × 10 × 10 × 10 = 10.000

📌 Negatif Üsler (Küçük Sayılar)

• 10⁻¹ = 1 / 10 = 0,1
• 10⁻² = 1 / 100 = 0,01
• 10⁻³ = 1 / 1.000 = 0,001
• 10⁻⁴ = 1 / 10.000 = 0,0001

Bu kurallar, bilimsel gösterimin temelini oluşturur.

2. Büyük Sayıları 10’un Kuvvetleriyle Yazma

Büyük sayılar, 10’un pozitif kuvvetleri ile yazılır. Bunun için:

1. Sayıyı en büyük basamağı 1 ile başlayan bir sayı olacak şekilde yaz.
2. Kaç basamak kaydırıldıysa, üslü ifade olarak yaz.

✅ Örnekler:

• 5.000 = 5 × 10³
• 120.000 = 1,2 × 10⁵
• 3.600.000 = 3,6 × 10⁶

📌 Özel Durum:

• 10, 100, 1.000 gibi sayılar zaten 10’un kuvvetleri şeklinde yazılabilir.
  • 100 = 10²
  • 1.000 = 10³
  • 1.000.000 = 10⁶

3. Küçük Sayıları 10’un Kuvvetleriyle Yazma

Küçük sayılar, 10’un negatif kuvvetleri ile gösterilir. Bunun için:

1. Sayıyı 1 ile başlayan bir sayı haline getir.
2. Ondalık noktayı kaç basamak kaydırdıysan, üslü ifade olarak yaz.

✅ Örnekler:

• 0,01 = 1 × 10⁻²
• 0,0005 = 5 × 10⁻⁴
• 0,000072 = 7,2 × 10⁻⁵

📌 Özel Durum:

• 0,1 = 10⁻¹
• 0,01 = 10⁻²
• 0,001 = 10⁻³

4. 10’un Kuvvetleri ile Çarpma ve Bölme İşlemleri

a) Çarpma Kuralı

📌 Kural:

✅ Örnekler:

• 10³ × 10² = 10⁵ = 100.000
• 10⁶ × 10⁴ = 10¹⁰
• 10⁻² × 10³ = 10¹ = 10

b) Bölme Kuralı

📌 Kural:

✅ Örnekler:

• 10⁵ ÷ 10² = 10³ = 1.000
• 10⁷ ÷ 10³ = 10⁴ = 10.000
• 10⁶ ÷ 10⁻² = 10⁸

5. Gerçek Hayatta Kullanımı

Bu yöntem, fizik, kimya, astronomi ve mühendislik gibi alanlarda büyük ve küçük sayılarla işlem yapmayı kolaylaştırır.

📌 Örnekler:

• Dünya’nın Güneş’e uzaklığı: 149.600.000 km
  • Bilimsel gösterim: 1,496 × 10⁸ km
• Bir atomun çapı: 0,0000000001 m
  • Bilimsel gösterim: 1 × 10⁻¹⁰ m

📌 Bu konuda öğrendiklerimiz:
✅ Büyük ve küçük sayıları 10’un kuvvetleriyle nasıl yazacağımızı öğrendik.
✅ Çarpma ve bölme işlemlerinde üsleri nasıl kullanacağımızı gördük.
✅ Gerçek hayatta bilimsel gösterimin kullanım alanlarını inceledik.

Bilimsel Gösterim

Bilimsel gösterim, çok büyük veya çok küçük sayıları kısa ve düzenli bir şekilde yazmak için kullanılan özel bir yöntemdir. Bu yöntem, matematik, fizik, kimya, mühendislik ve astronomi gibi birçok alanda kullanılır.

1. Bilimsel Gösterimin Tanımı

Bir sayı bilimsel gösterimde şu formatta yazılır:

Burada:

• a → 1 ile 10 arasında bir ondalık sayı (1 ≤ a < 10)
• n → Tam sayı kuvveti (10’un üssü)

✅ Örnek:

• Bilimsel gösterim: 3,2 × 10⁵
• Açılımı: 3,2 × 100.000 = 320.000

2. Büyük Sayıları Bilimsel Gösterimle Yazma

Büyük sayıları bilimsel gösterimle yazmak için:

1. Sayıyı 1 ile 10 arasında bir sayı olacak şekilde düzenle.
2. Ondalık virgülü kaydırdığın basamak sayısını üs olarak yaz.

📌 Örnekler:

• 500.000 → 5 × 10⁵
• 12.000.000 → 1,2 × 10⁷
• 4.600.000 → 4,6 × 10⁶

Adım Adım Örnek:
📌 345.000 sayısını bilimsel gösterime çevirelim.

1. 345.000 → 3,45 olacak şekilde düzenlenir.
2. Virgül 5 basamak sola kaydırıldığı için üs 5 olur.
   ✅ Cevap: 3,45 × 10⁵

3. Küçük Sayıları Bilimsel Gösterimle Yazma

Küçük sayıları bilimsel gösterimle yazmak için:

1. Sayıyı 1 ile 10 arasında bir sayı olacak şekilde düzenle.
2. Ondalık virgülü kaydırdığın basamak sayısını negatif üs olarak yaz.

📌 Örnekler:

• 0,0004 → 4 × 10⁻⁴
• 0,000087 → 8,7 × 10⁻⁵
• 0,0023 → 2,3 × 10⁻³

Adım Adım Örnek:
📌 0,00076 sayısını bilimsel gösterime çevirelim.

1. 0,00076 → 7,6 olacak şekilde düzenlenir.
2. Virgül 4 basamak sağa kaydırıldığı için üs -4 olur.
   ✅ Cevap: 7,6 × 10⁻⁴

4. Bilimsel Gösterimde İşlemler

Bilimsel gösterimde çarpma ve bölme işlemleri için bazı kurallar vardır.

a) Çarpma İşlemi

📌 Kural:

✅ Örnek:

1. Katsayılar çarpılır: 3 × 2 = 6
2. Üsler toplanır: 4 + 3 = 7
   ✅ Sonuç: 6 × 10⁷

b) Bölme İşlemi

📌 Kural:

✅ Örnek:

• Katsayılar bölünür: 6 ÷ 2 = 3
• Üsler çıkarılır: 5 – 2 = 3
  ✅ Sonuç: 3 × 10³

5. Gerçek Hayatta Bilimsel Gösterimin Kullanımı

Bilimsel gösterim, çok büyük ve çok küçük sayılarla işlem yapmayı kolaylaştırır.

📌 Örnekler:

• Dünya ile Güneş arasındaki mesafe:
  • 149.600.000 km
  • Bilimsel gösterimi: 1,496 × 10⁸ km
• Bir atomun çapı:
  • 0,0000000001 m
  • Bilimsel gösterimi: 1 × 10⁻¹⁰ m
• Işık hızı:
  • 299.792.458 m/s
  • Bilimsel gösterimi: 3 × 10⁸ m/s

📌 Bu konuda öğrendiklerimiz:
✅ Bilimsel gösterimin ne olduğunu ve nasıl yazıldığını öğrendik.
✅ Büyük ve küçük sayıları bilimsel gösterime çevirdik.
✅ Bilimsel gösterimde çarpma ve bölme işlemlerini inceledik.
✅ Gerçek hayatta bilimsel gösterimin kullanım alanlarını gördük.

8. Sınıf Matematik Üslü İfadeler Örnek Sorular

1. Büyük Sayıları Bilimsel Gösterime Çevirme

📌 Soru 1: 567.000.000 sayısını bilimsel gösterimle ifade ediniz.

Çözüm:

1. Sayıyı 1 ile 10 arasında bir sayı olacak şekilde düzenleyelim:
   • 5,67 olacak şekilde ayarlıyoruz.
2. Virgülü 8 basamak sola kaydırdık, bu yüzden üslü ifade 10⁸ olur.

✅ Cevap: 5,67 × 10⁸

2. Küçük Sayıları Bilimsel Gösterime Çevirme

📌 Soru 2: 0,000042 sayısını bilimsel gösterimle ifade ediniz.

Çözüm:

1. Sayıyı 1 ile 10 arasında bir sayı olacak şekilde düzenleyelim:
   • 4,2 olacak şekilde ayarlıyoruz.
2. Virgülü 5 basamak sağa kaydırdık, bu yüzden üslü ifade 10⁻⁵ olur.

✅ Cevap: 4,2 × 10⁻⁵

3. Bilimsel Gösterimde Çarpma İşlemi

📌 Soru 3:

işleminin sonucunu bulunuz.

Çözüm:

1. Katsayıları çarpalım: 3 × 2 = 6
2. Üsleri toplayalım: 5 + 3 = 8

✅ Cevap: 6 × 10⁸

4. Bilimsel Gösterimde Bölme İşlemi

📌 Soru 4:

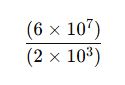
işleminin sonucunu bulunuz.

Çözüm:

1. Katsayıları bölelim: 6 ÷ 2 = 3
2. Üsleri çıkaralım: 7 – 3 = 4

✅ Cevap: 3 × 10⁴

5. Bilimsel Gösterimle Toplama İşlemi

📌 Soru 5:

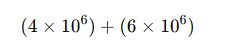
işleminin sonucunu bulunuz.

Çözüm:

1. Üsler aynı olduğu için katsayıları toplayalım:
   • 4 + 6 = 10
2. Sonuç: 10 × 10⁶
3. Bilimsel gösterim formatına uygun hale getirelim:
   • 10 × 10⁶ = 1 × 10⁷

✅ Cevap: 1 × 10⁷

6. Bilimsel Gösterimde Farklı Üslü Sayıları Toplama

📌 Soru 6:

işleminin sonucunu bilimsel gösterimle yazınız.

Çözüm:

1. Üsler farklı olduğunda, önce üsleri eşitlememiz gerekir.
   • 3 × 10⁴ = 0,3 × 10⁵ (10⁵ formatına çevrildi)
2. Katsayıları toplayalım:
   • 0,3 + 2 = 2,3
3. Sonuç: 2,3 × 10⁵

✅ Cevap: 2,3 × 10⁵

7. Küçük Sayılarla Bilimsel Gösterimde Çarpma İşlemi

📌 Soru 7:

işleminin sonucunu bilimsel gösterimle yazınız.

Çözüm:

1. Katsayıları çarpalım: 2 × 5 = 10
2. Üsleri toplayalım: -3 + (-2) = -5
3. Sonuç: 10 × 10⁻⁵
4. Bilimsel gösterime uygun hale getirelim:
   • 10 × 10⁻⁵ = 1 × 10⁻⁴

✅ Cevap: 1 × 10⁻⁴

8. Bilimsel Gösterimle Bölme İşlemi

📌 Soru 8:

işleminin sonucunu bulunuz.

Çözüm:

1. Katsayıları bölelim: 4 ÷ 2 = 2
2. Üsleri çıkaralım: 6 – 2 = 4
3. Sonuç: 2 × 10⁴

✅ Cevap: 2 × 10⁴

9. Büyük Sayıyı Bilimsel Gösterime Çevirme

📌 Soru 9: 23.700.000.000 sayısını bilimsel gösterimle ifade ediniz.

Çözüm:

1. Sayıyı 1 ile 10 arasında bir sayı olacak şekilde düzenleyelim:
   • 2,37 olacak şekilde ayarlıyoruz.
2. Virgülü 10 basamak sola kaydırdık, bu yüzden üslü ifade 10¹⁰ olur.

✅ Cevap: 2,37 × 10¹⁰

10. Küçük Sayıyı Bilimsel Gösterime Çevirme

📌 Soru 10: 0,0000000254 sayısını bilimsel gösterimle ifade ediniz.

Çözüm:

1. Sayıyı 1 ile 10 arasında bir sayı olacak şekilde düzenleyelim:
   • 2,54 olacak şekilde ayarlıyoruz.
2. Virgülü 8 basamak sağa kaydırdık, bu yüzden üslü ifade 10⁻⁸ olur.

✅ Cevap: 2,54 × 10⁻⁸

📌 10 soru boyunca şunları öğrendik:
✔ Büyük ve küçük sayıları bilimsel gösterime nasıl çevireceğimizi öğrendik.
✔ Bilimsel gösterimde çarpma ve bölme işlemlerini yaptık.
✔ Toplama ve çıkarma işlemlerinde üsleri nasıl eşitleyeceğimizi gördük.