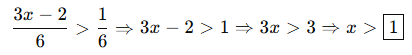AYT Matematik Basit Eşitsizlikler Konu Anlatımı ve Örnek Sorular

AYT Matematik Basit Eşitsizlikler 

📘 Tanım:

İki matematiksel ifadeyi karşılaştırmak için kullanılan

• Küçüktür (<),
• Büyüktür (>),
• Küçük eşittir (≤),
• Büyük eşittir (≥)

sembolleriyle kurulan ifadelere eşitsizlik denir.

Bu eşitsizliklerde genellikle bilinmeyen bir değişken (örneğin x) olur ve bu değişkenin aldığı değerler kümesini bulmak hedeflenir.

🎯 Basit Eşitsizlik ne demektir?

Adı üstünde “basit”, yani genellikle:

• Bir bilinmeyenli,
• Birinci dereceden,
• Doğrusal eşitsizliklerdir.

Örnekler:

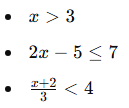
📌 Neden Önemli?

Basit eşitsizlikler:

• AYT’de mutlak değerli, karmakarışık eşitsizliklerin temelidir
• Sayı doğrusunda çözüm aralığı çizmeyi öğretir
• Denklem çözme ve mantıksal yorumla birleşir
• Kümeler, fonksiyonlar, parabol, logaritma gibi konularla doğrudan bağlantılıdır

🔍 Ünitedeki Alt Başlıklar

1. Eşitsizlik Kavramı ve Sembolleri
2. Doğrusal (Birinci Dereceden) Eşitsizliklerin Çözümü
3. Eşitsizliklerin Sayı Doğrusunda Gösterimi
4. Eşitsizliklerin Kapsadığı Değerler Kümesi
5. Çarpanlara Ayırarak Eşitsizlik Çözme (İşaret Tablosu)
6. Eşitsizliklerin Grafiksel Yorumu
7. AYT Düzeyinde Eşitsizlik Problemleri

Eşitsizlik Kavramı ve Sembolleri

İki ifadeyi büyüklük ya da küçüklük yönüyle karşılaştıran ve bu karşılaştırmayı eşitlik olmaksızın ifade eden matematiksel ifadelere eşitsizlik denir.

🔹 Eşitsizlik Sembolleri:

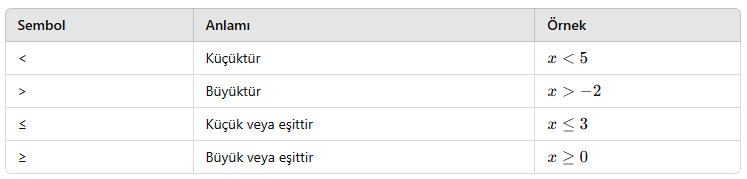
Bu semboller yardımıyla bir değişkenin aldığı değerler hakkında sınır koyarız.

🎯 Eşitsizlikler Ne Anlatır?

• x<5 → x, 5’ten küçük değerler alabilir. (5 dâhil değil)

• x≥−3 → x, -3 ve daha büyük değerler alabilir. (eşitlik dâhil)

🧠 Matematiksel Yorumu:

Eşitsizlik, bir çözüm kümesi belirtir.
Yani sadece bir değer değil, birçok çözüm olabilir.

Örneğin:

📏 Küme Gösterimiyle Yazım:

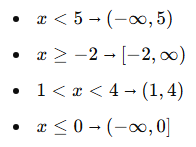
🎓 Örnek 1:

Aşağıdaki eşitsizliğin küme gösterimi nedir?

x≥2

Cevap:
[2,∞) ✅

🎓 Örnek 2:

x < -3 eşitsizliğinin çözüm kümesi sayı doğrusunda nasıl gösterilir?

Cevap:
Açık yuvarlak (çünkü -3 dâhil değil)
→ Sola doğru ok çizilir
→ (−∞,−3) aralığı ✅

🔎 Eşitsizliklerde Dikkat Edilecekler:

• Açık aralık ( ) → eşitlik yok

• Kapalı aralık [ ] → eşitlik var

• Sayı doğrusunda açık yuvarlak (eşitlik yok), dolu yuvarlak (eşitlik var)

Doğrusal (Birinci Dereceden) Eşitsizliklerin Çözümü

📘 Tanım:

Doğrusal eşitsizlik, içinde bilinmeyen bulunan ve bu bilinmeyenin birinci dereceden olduğu eşitsizlik türüdür.

Genel hali:

🎯 Temel Kurallar:

1. Eşitsizlik, denklem gibi çözülebilir

2. Her iki tarafa aynı işlem (toplama, çıkarma, çarpma, bölme) yapılabilir

3. Ancak ❗❗
   Eğer her iki taraf negatif bir sayı ile çarpılır veya bölünürse, eşitsizlik yönü değiştirilir

🔄 Eşitsizlik Yönü Değişir mi?

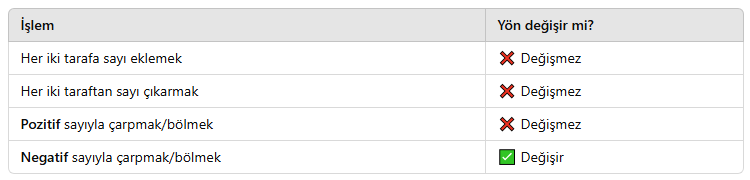
🎓 Örnek 1:

Çözüm:

🎓 Örnek 2:

Çözüm:

🎓 Örnek 3 – Kesirli:

​

Ortak payda: 6

🎓 Örnek 4 – Sayı Doğrusuna Göre:

Bu bir bileşik eşitsizliktir, aynı anda iki şartı sağlar.

Adım adım:

​

📏 Küme Gösterimiyle Çözüm:

• Açık uç: ( veya ) → eşitlik yok

• Kapalı uç: [ veya ] → eşitlik var

🧠 AYT İpuçları:

• Negatif ile çarparken yön değiştirmeyi unutma ❗

• Kesirli eşitsizliklerde ortak payda ile sadeleştirme işlem kolaylaştırır

• Sayı doğrusunda gösterim sorularına dikkat (özellikle bileşik eşitsizliklerde)

Eşitsizliklerin Sayı Doğrusunda Gösterimi

📘 Tanım:

Bir eşitsizlik çözümünün hangi aralıktaki sayıları kapsadığını, görsel olarak sayı doğrusu üzerinde gösterme işlemidir.

Bu gösterim, özellikle:

• Eşitsizliklerde çözüm kümesini anlamak

• İki veya daha fazla eşitsizliği birleştirmek

• Kümelerle bağ kurmak
  için çok önemlidir.

🎯 Gösterim Kuralları:

🔵 Açık Daire – ( )

• Eşitlik yoksa (örneğin: x>3 veya x<5)
  → Sayı doğrusunda o noktada açık daire konur.

🔴 Kapalı Daire – [ ]

• Eşitlik varsa (örneğin: x≥3, x≤5)
  → Sayı doğrusunda o noktada dolu daire (kapalı yuvarlak) kullanılır.

🔀 Ok Yönü

• x > a : sağa doğru ok

• x < a : sola doğru ok

🎓 Örnek 1:

x>2

→ Sayı doğrusunda:

• 2’nin üzerinde açık daire

• Sağa doğru ok

• Küme gösterimi: (2,∞)

🎓 Örnek 2:

x≤−1

→ Sayı doğrusunda:

• -1 üzerinde kapalı daire

• Sola doğru ok

• Küme gösterimi: (−∞,−1]

🎓 Örnek 3: (Bileşik Eşitsizlik)

−4<x≤2

→ Sayı doğrusunda:

• -4 → açık daire

• 2 → kapalı daire

• Aradaki tüm değerleri kapsayan çizgi

• Küme gösterimi: (−4,2]

📏 Küme Gösterimi – Dönüşümler Tablosu:

🧠 AYT Düzeyinde Dikkat Et:

• Bileşik eşitsizliklerde ortak aralık dikkatle gösterilmeli

• Özellikle açık/kapalı sınırları karıştırmak çok yaygın hatadır

• Görsel sorularda şekil üzerinden doğru yorum yapılmalı (ok yönleri!)

Eşitsizliklerin Kapsadığı Değerler Kümesi

📘 Tanım:

Bir eşitsizlik çözüldükten sonra, değişkenin alabileceği tüm değerler bir küme şeklinde ifade edilir. Bu kümeye çözüm kümesi denir ve genellikle:

• Küme paranteziyle

• Aralık biçimiyle

• Sayı doğrusuyla birlikte
  gösterilir.

🔹 Kapsamlı Aralık Gösterimleri:

🔍 Rasyonel ve Tam Sayılarla Gösterim:

Eğer x ∈ ℤ (tam sayılar kümesi) denmişse:

Eğer x ∈ ℚ (rasyonel sayılar kümesi):
→ Bu aralıkta sonsuz rasyonel sayı vardır: 1.1, 1.01, 1.99, 2.5…

🎯 AYT Düzeyinde Soru Örnekleri

Soru 1:

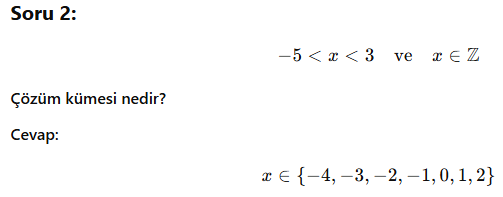
🧠 Dikkat Et:

• Eşitsizliğin çözüm kümesi, hangi sayı kümesi içinde verildiğine göre değişebilir

• ℝ (gerçek sayılar), ℚ (rasyonel), ℤ (tam sayılar), ℕ (doğal sayılar) → bunlar seçenekleri etkiler

• Açık–kapalı aralıkları kümede doğru yansıtmalısın

Çarpanlara Ayırarak Eşitsizlik Çözme (İşaret Tablosu Yöntemi)

📘 Tanım:

Bir eşitsizlik ifadesi çarpanlara ayrıldığında, her çarpanın işareti ayrı ayrı incelenerek ifadenin pozitif veya negatif olduğu aralıklar bulunur. Bu yöntem “işaret tablosu” adıyla bilinir.

🎯 Neden Önemlidir?

Çünkü:

• İkinci dereceden eşitsizlikler

• Çarpanlı ifadeler

• Rasyonel ifadeler (kesirli eşitsizlikler)
  ancak bu yolla doğru şekilde çözülebilir.

🔄 İşaret Tablosu Adımları:

1. Eşitsizliği sıfıra eşitle

2. Tüm ifadeyi çarpanlarına ayır

3. Kritik noktaları (sıfır yapan değerler) bul

4. Sayı doğrusunda bu noktaları işaretle

5. Aralıkları tek tek test ederek işaret belirle

6. Eşitsizliğin yönüne göre çözüm kümesini yaz

🧠 AYT’de Dikkat Edilmesi Gerekenler:

• Rasyonel eşitsizliklerde payda asla sıfır olamaz!

• İşaret tablosu çizmeden yorum yapma

• Kritik değerlerde eşitlik varsa (≤, ≥), kök dâhil edilir

• Pay ve paydanın işareti ayrı ayrı değerlendirilmelidir

• Fazla kesirli ifadelerde işaret çarpımı çok önemlidir

Eşitsizliklerin Grafiksel Yorumu ve AYT Düzeyi Problemler

📘 Grafiksel Yorum Nedir?

Eşitsizliklerin çözüm kümesini sadece sayı doğrusunda değil, grafikler ve fonksiyonlar üzerinden yorumlamak da mümkündür.

Bu bölümde özellikle:

• Doğrunun üzerinde/altında kalan alanlar

• Parabolün kollarına göre işaretler

• Alan – aralık soruları

• Gerçek hayat senaryoları (maliyet, üretim, süre vs.)
  gibi sorular karşımıza çıkabilir.

🔹 1. Doğrusal Fonksiyonlarda Eşitsizlik

🎓 Örnek:

🔹 2. Parabolde Eşitsizlik

Parabolün kolları yukarıdaysa:

• f(x) > 0 → parabolün x-ekseninin üstü

• f(x) < 0 → parabolün x-ekseninin altı

🎓 Örnek:

f(x) = x² – 4x + 3 için:
f(x) < 0 eşitsizliğini sağlayan x değerleri nedir?

Parabolü çöz:

İşaret tablosu:

• Kökler arasında: negatif

• Köklerin dışında: pozitif (kollar yukarı çünkü a > 0)

Cevap: (1,3)

🔹 3. Gerçek Hayat Problemleri (AYT Düzeyi)

🎓 Örnek 1:

Bir ürünün maliyeti (TL) f(x) = 3x + 10 ile veriliyor.
Kar elde etmek için ürün en az 25 TL’ye satılmalıdır.
Buna göre, x en az kaç olmalıdır?

Çözüm:

📌 En az 5 birim üretildiğinde maliyet 25 TL’yi geçer.

🎓 Örnek 2:

Bir okuldaki öğrenci sayısı x olsun. Her öğrenci 15 TL öderse toplam gelir en az 900 TL olmalıdır.
Buna göre x’in alabileceği en küçük tam sayı değeri nedir?

🧠 AYT’de Dikkat Et:

• Fonksiyon grafikleri ile eşitsizlik yorumlaması birleştirilebilir

• Parabolün kollarının yönü çok önemlidir

• Gerçek hayat sorularında “en az”, “en çok”, “kar etmek için” gibi ifadeler genelde eşitsizlik gerektirir

• Sonuçlar genellikle tam sayı ya da belirli bir kümeye ait sayı olarak sorulur

AYT Matematik Basit Eşitsizlikler Testi