AYT Matematik Binom ve Olasılık Konu Anlatımı

Bu ünitede, iki ana başlık işlenir:

1. Binom Açılımı:
    İki terimli ifadelerin üs alma kuralına göre açılması
    

2. Olasılık:
    Belirli bir olayın olma ihtimalinin matematiksel ifadesi
    ​

🔹 Ünitenin Alt Başlıkları:

A) Binom Açılımı

1. Binom Açılımı Tanımı

2. Binom Katsayıları ve Pascal Üçgeni

3. Genel Terim ve Terim Sayısı

4. Belirli Terimi Bulma ve Uygulamalar

B) Olasılık

5. Olasılık Tanımı ve Temel Kurallar

6. Birleşik Olaylar

7. Koşullu Olasılık ve Problem Çözümü

🎯 AYT’de Bu Konular Nasıl Sorulur?

• Binom açılımında belirli terimin katsayısı

• Belirli terimin kaçıncı terim olduğu

• Olasılıkta klasik tanım, zar-deste-torba problemleri

• Ayrık olaylar, birlikte olma-olmama durumu

• Olayların kesişim ve birleşim olasılıkları

• Koşullu olasılık soruları

Binom Açılımı Tanımı

📘 Binom Nedir?

Binom, iki terimli bir ifadedir.
Örneğin:

Bu ifadelerin açılımında her terimin bir katsayısı, a’lı ve b’li kısmı olur.

🧠 Binom Açılımı Kuralı:

Burada:

🎯 Genel Özellikler:

📌 Not: Negatif ve değişkenli ifadelerde dikkat!

Örneğin:

Binom Katsayıları ve Pascal Üçgeni

📘 Binom Katsayıları Nedir?

Bu katsayılar:

• Kombinasyonla hesaplanır

• Pascal Üçgeni ile kolayca bulunabilir

🧠 Kombinasyon ile Katsayı Hesabı:

🎯 Pascal Üçgeni:

Katsayılar üçgen şeklinde düzenlenebilir:

• Her satırın kenarı 1

• İç terimler: üstteki iki terimin toplamı

• Satır n → 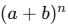 açılımındaki katsayılar

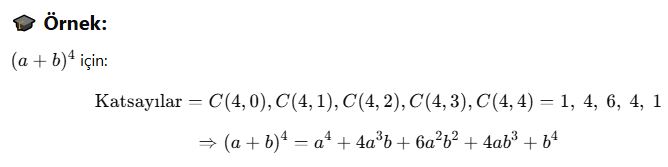
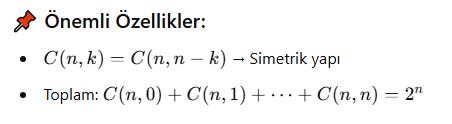
Genel Terim ve Terim Sayısı

📘 A. Terim Sayısı

​

📘 B. Genel Terim Formülü

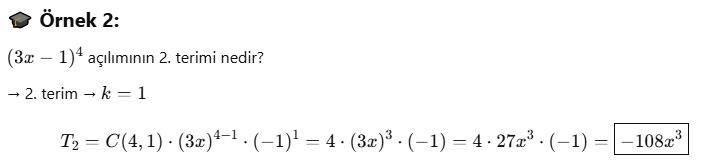
📘 C. Belirli Kuvvetli Terim Bulma:

Belirli Terimi Bulma ve Uygulamalar

📘 A. Belirli Kuvvetli Terimi Bulma

🎓 Örnek 1:

📘 B. Sabit Terimi Bulma

Sabit terim → x’siz terim
Yani:

🎓 Örnek 2:

📘 C. En Büyük ve En Küçük Terim Soruları

• Terim sayısı: n+1

• En büyük katsayı genelde orta terimdedir:

Olasılık Tanımı ve Temel Kurallar

📘 Olasılık Nedir?

Bir olayın gerçekleşme olasılığı:

​​

Burada:

• $\text{P}(A)$: A olayının olma olasılığı

• Sonuçlar eş olasılıklı olmalı (her biri aynı ihtimalle gerçekleşiyor)

📘 Temel Kavramlar:

🎯 Temel Kurallar:

1. Tüm olasılıklar toplamı:

2. A olayının olmama olasılığı:

3. Birleşik olay:

🎓 Örnek 1:

Bir zar atılıyor.
Tek sayı gelme olasılığı nedir?

• Örnek uzay: {1, 2, 3, 4, 5, 6}

• İstenen: {1, 3, 5} → 3 durum

🎓 Örnek 2:

Bir deste karttan (52 kart) rastgele çekiliyor.
Kupa gelme olasılığı nedir?

• Kupa sayısı: 13

📌 Dikkat Edilecek Noktalar:

• Tüm durumları doğru saymak (Örnek uzayı iyi belirlemek)

• Eş olasılıklı mı? Soruda belirtilmeli

• “En az – en çok” gibi ifadeler iyi yorumlanmalı

Mini Alıştırmalar:

1. Bir zar atıldığında 4 gelme olasılığı?

2. Bir torbada 3 kırmızı, 2 mavi, 1 yeşil top var. Rastgele çekilen topun kırmızı olma olasılığı?

3. Bir zar atıldığında çift sayı gelmeme olasılığı?

Birleşik Olaylar (A ∪ B, A ∩ B)

📘 A. Kesişim ve Birleşim Kavramları

🎯 Temel Kural:

→ “Ya A ya B” olasılığı
→ Ortak kısım iki kez sayıldığından çıkarılır

🎯 Bağımsız ve Ayrık Olaylar:

• Ayrık olaylar: Ortak durum yok →

• Bağımsız olaylar: Birinin olma durumu diğerini etkilemez
   (bir zar ve bir madeni para örneği gibi)

🎓 Örnek 1:

Bir zar atıldığında:

• A: Tek sayı gelmesi → {1, 3, 5}

• B: 2’nin katı gelmesi → {2, 4, 6}

🎓 Örnek 2:

Bir deste karttan çekilen kart:

• A: Kupa → 13 kart

• B: Papaz → 4 kart

• Kupa papaz → 1 kart (kesişim)

🧠 P(A ∩ B) = P(A) · P(B)

→ Bu formül sadece bağımsız olaylar için geçerlidir.

Mini Alıştırmalar:

1. Bir zar atılıyor.
    A: 1 veya 2 gelmesi
    B: Tek sayı gelmesi
    

2. Bir torbada 4 kırmızı, 3 mavi, 2 yeşil top var.
    A: kırmızı
    B: mavi
    

Koşullu Olasılık ve Problem Çözümü

📘 Koşullu Olasılık Nedir?

Bir olayın, başka bir olayın gerçekleşmiş olması durumunda olasılığına denir.

🎓 Örnek 1:

Bir zar atılıyor.
B: Çift sayı gelmesi
A: 2 gelmesi

🎓 Örnek 2:

Bir sınıfta 7 erkek, 5 kız öğrenci var.
Rastgele bir öğrenci seçildiği biliniyor → seçilen kişi kız.
Bu kişinin gözlüklü olma olasılığı nedir?

→ Toplam kız = 5
→ Gözlüklü kız = 2
Koşullu olasılık:

📘 Koşullu Olasılığın Mantığı:

• Önce “koşul” olan olayın içinden düşün

• Sonra bu alt kümede “istenen” olayı say

• Yeni örnek uzayı = koşulun örnek uzayı

Mini Problemler:

1. Bir kart çekiliyor.
   A: Sinek gelmesi
   B: Siyah kart gelmesi
   

2. Bir torbada 3 kırmızı, 5 mavi, 2 yeşil top var.
   Bir top çekiliyor, kırmızı olduğu biliniyor.
   Bu topun tek sayılı numara taşıma olasılığı 23\frac{2}{3}32​ ise,
   kaç kırmızı top tek sayılıdır?

AYT Binom ve Olasılık Testi

Cevap anahtarı en altta
Her soru farklı bir alt başlıktan seçilmiştir

1. (Binom Açılımı – Temel Açılım)

2. (Binom Katsayıları)

  açılımında en büyük katsayı kaçtır?

A) 20
B) 15
C) 6
D) 30

3. (Genel Terim)

4. (Sabit Terim)

  açılımında sabit terim nedir?

A) 10
B) 15
C) 20
D) 30

5. (Olasılık – Klasik Tanım)

Bir zar atılıyor. 2 gelme olasılığı nedir?

6. (Birleşik Olaylar)

Bir zar atıldığında
A: Tek sayı gelmesi
B: 2 veya 4 gelmesi

7. (Olasılık – Tamamlayıcı Olay)

Bir zar atıldığında çift sayı gelmeme olasılığı nedir?

8. (Koşullu Olasılık)

Bir zar atılıyor. Tek sayı geldiği biliniyor.
Gelen sayının 3 olma olasılığı nedir?

9. (Pascal Üçgeni)

Pascal üçgeninde 5. satırdaki 3. sayı nedir?

A) 6
B) 10
C) 20
D) 15

10. (Binom – Belirli Kuvvetli Terim)

A) –270
B) –90
C) 90
D) 270