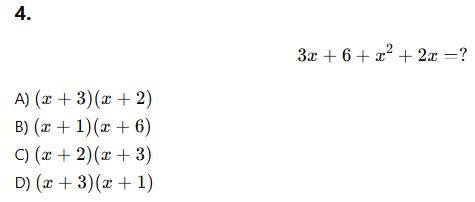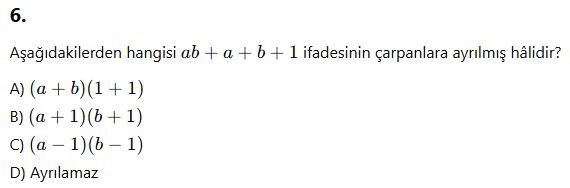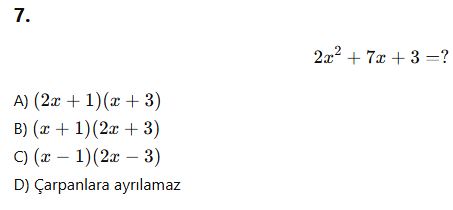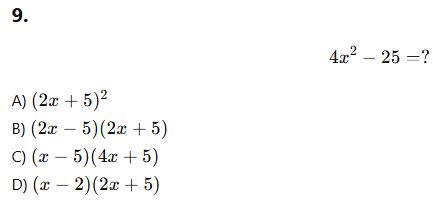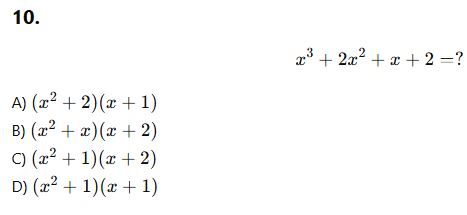AYT Matematik Çarpanlara Ayırma Konu Anlatımı

Bu konu, hem AYT sorularında tek başına gelir hem de rasyonel ifadeler, eşitsizlikler, polinomlar ve fonksiyonlar gibi birçok konuda temel oluşturur. Sınavlarda çokça çıkan ve işlem pratiği gerektiren bir ünitedir.

📌 Amaç Nedir?

Çarpanlara ayırma, bir matematiksel ifadeyi daha küçük parçalara (çarpanlara) bölerek sadeleştirme ve işlem kolaylığı sağlama yöntemidir.

Örnek:

Bu dönüşüm sayesinde:

• Eşitlik daha kolay çözülür

• Denklemlerin kökleri bulunur

• Eşitsizlikler çözülür

• Paydalarda sadeleştirme yapılabilir

📚 Çarpanlara Ayırma Ünitesinin Alt Başlıkları:

1. Ortak Çarpan Parantezine Alma

2. Özel Çarpanlar:

   • a² – b²

   • a² ± 2ab + b²

3. Gruplandırarak Ayırma

4. Rasyonel İfadelerle Ayırma

5. İkinci Dereceden İfadelerin Ayırımı

6. AYT Seviyesinde Uygulama Soruları

🎓 Örnek – Basit Dönüşüm:

Soru:

Cevap:

AYT’de Neler Sorulur?

• Çok terimli ifadelerin sadeleştirilmesi

• İkinci ve üçüncü dereceden ifadelerin kök bulma yoluyla ayırımı

• Karmaşık eşitsizliklerin çözüm öncesi çarpanlara ayrılması

• Fonksiyon tanım kümesi – sıfır yapan değerler

• Sadeleştirme içeren rasyonel ifadeler

Ortak Çarpan Parantezine Alma

Bu yöntem, çarpanlara ayırmanın en temel ve en çok kullanılan yoludur. Özellikle her terimde ortak olan bir ifade varsa, onu parantez dışına alarak ifade sadeleştirilir.

📘 Tanım:

Birden fazla terimli bir ifadede, tüm terimlerde ortak olan bir çarpanı parantez dışına alma işlemidir.

Burada a, ortak çarpan olarak dışarı alınmıştır.

🧠 Neden Önemli?

• İşlemi sadeleştirir

• Eşitlik ve denklemlerde kolaylık sağlar

• Birçok çarpanlara ayırma yöntemiyle birlikte kullanılır

🔹 Kural:

Eğer tüm terimlerde bir ortak çarpan varsa:

🎓 Örnek 1:

🎓 Örnek 2:

🎓 Örnek 3 (Değişkenli ortak çarpan):

Uygulamalı Mini Test:

Sadeleştiriniz:

✅ Çözümler:

AYT’de Dikkat Edilecekler:

• Sayısal ve değişkenli ortak çarpanları birlikte görmeye alış

• Karmaşık ifadelerde önce sadeleştir, sonra ayır

• Genellikle diğer ayırma yöntemleriyle birlikte kullanılır

• Parantez açıp tekrar dağıtmak, doğru işlem yaptığını kontrol etmeni sağlar

Özel Çarpanlar

Bu bölümde bazı ifadeleri ezberlenmiş kalıplar yardımıyla hızlıca çarpanlarına ayırmayı öğreneceğiz. Özellikle AYT’de işlem hızını ve dikkat seviyesini ölçen bu kalıplar sınavın vazgeçilmezidir.

📘 A. İki Kare Farkı (a² − b²) Kalıbı

🎓 Örnek:

🎓 Örnek:

❗ Dikkat:

İki kare farkı, sadece iki terim varsa ve her biri tam kare ise uygulanabilir.

📘 B. Tam Kare Açılımı

1. Pozitif:

2. Negatif:

🎓 Örnek:

🎓 Örnek:

🎯 Bu Kalıplar Nasıl Ayırt Edilir?

1. İki terimli ifade ve her terim kare mi? → muhtemelen iki kare farkı

2. Üç terimli, 1. ve 3. terim kare, ortadaki iki katı mı? → tam kare açılımı

Uygulamalı Mini Test:

Çarpanlarına ayırınız:

✅ Cevaplar:

AYT’de Dikkat Edilecekler:

• Bu kalıplar soru içinde gizlenmiş olabilir. Gözün hemen tanımalı.

• Genişletip kontrol etmek, doğru yaptığını test eder.

• İfadeyi tam kare/sayı şeklinde düzenlemek bazen sorunun çözümüdür.

• Karmaşık eşitsizlik ve rasyonel sadeleştirme sorularında sıkça çıkar.

Gruplandırarak Çarpanlara Ayırma

Bu yöntem, özellikle 4 terimli ifadelerde ve bazen 3 terimli ama çarpan bulunamayan ifadelerde kullanılır. Ortak çarpan parantezine alma mantığının genelleştirilmiş hâlidir.

📘 Kural:

1. Terimleri uygun gruplara ayır

2. Her grupta ortak çarpanı paranteze al

3. Ortak parantezi kullanarak çarpanlara ayır

🎓 Örnek 1:

İlk 2 terim ve son 2 terim gruplanır:

🎓 Örnek 2:

🎓 Örnek 3:

❗ Dikkat:

• Gruplama her zaman “ilk 2 – son 2” olmayabilir!

• Gerekirse terimlerin sırasını değiştirerek uygun gruplama yapılabilir

• Ortak parantez her iki grupta aynı çıkmazsa, farklı yöntem denenmelidir

Uygulamalı Mini Test:

Aşağıdaki ifadeleri çarpanlarına ayırınız:

✅ Cevaplar:

AYT’de Dikkat Edilecekler:

• 4 terimli ifadelerde gruplandırma refleksi kazanılmalı

• Ortak parantez yoksa özel çarpan kalıpları denenmeli

• Gruplama, polinom ve kesirli sadeleştirme sorularında da çıkar

• Gerekirse ifadeyi yeniden düzenleyerek ayırma imkânı yarat

Rasyonel İfadelerde Çarpanlara Ayırma ve Sadeleştirme

📘 Tanım:

Rasyonel ifadeler, kesir biçiminde yazılmış cebirsel ifadelerdir.
Bunları sadeleştirmek için hem payı hem paydayı çarpanlarına ayırır, ortak çarpanları sadeleştiririz.

🔸 Amaç:

• İşlem kolaylığı

• Tanım kümesi belirleme

• Eşitsizlik çözümü

• Fonksiyon sadeleştirme

🎓 Temel Örnekler

Örnek 1:

​

Adım adım çarpanlarına ayıralım:

Sadeleştir:

Örnek 2:

​

Sadeleştir:

📌 Tanım Kümesi Notu:

Sadeleştirdiğin çarpan paydayı 0 yapan değerse, bu değeri sonuçtan çıkartmalısın.
Yani sadeleşse bile tanım kümesinden atılır.

AYT’de En Çok Çıkan Soru Tipleri:

• “Aşağıdakilerden hangisi sadeleştirildiğinde elde edilir?”

• Tanım kümesini dışlayan özel değerler

• Rasyonel ifadeyle eşitsizlik çözümü (işaret tablosu)

• Fonksiyonlarda tanımsızlık noktaları

🎓 Mini Uygulama Sorusu:

Sadeleştir:

​

Çözüm:

Sadeleştirilmiş:

Uygulamalı Mini Test:

Sadeleştiriniz (ve tanım kümesini belirtiniz):

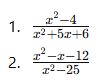
✅ Cevaplar:

İkinci Dereceden İfadelerin Çarpanlara Ayrılması

Bu bölümde klasik  tipindeki ifadeleri kök bulma yöntemiyle çarpanlarına ayıracağız. Özellikle AYT’de denklemler, eşitsizlikler ve fonksiyonların tanım kümelerinde sıkça karşımıza çıkar.

📘 Genel Biçim:

​

Çarpanlarına ayrılmış hâli:

Kökleri bulmak için:

📌 Tam Kare Olmayanlar:

Kökler rasyonel değilse, çarpanlara ayırmak yerine kökleri bulup işlem yapma tercih edilir.

AYT’de Dikkat Edilecekler:

• Çarpanlara ayırma, denklem/ifade üzerinde işlem yapma kolaylığı sağlar

• Özellikle tanım kümesi, eşitsizlik ve sadeleştirme sorularında sık çıkar

• Kökler rasyonel değilse, ifadenin çarpanlara ayrılmadığı kabul edilir

• Dikkat! Bazı sorularda faktör eşliğinde yazma gerekir:

Uygulamalı Mini Test:

Aşağıdaki ifadeleri çarpanlarına ayırınız:

AYT Çarpanlara Ayırma Testi (10 Soru)