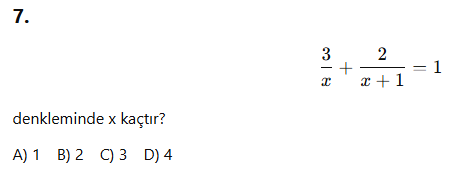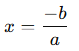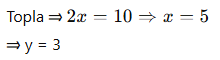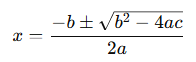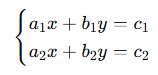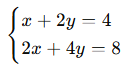AYT Matematik Denklem Çözme Konu Anlatımı

Denklem çözme, matematikte bilinmeyeni bulmaya yönelik yapılan en temel işlemlerden biridir. AYT seviyesinde bu konu;

• Daha karmaşık yapılı denklemler,

• Mutlak değerli, köklü, üslü ifadeler içeren eşitlikler,

• Denklem sistemleri ve mantıksal yorumlar,

• Denklemin kökü, tanım kümesi, çözüm kümesi,

• Çok adımlı denklem dönüşümleri
  gibi alt başlıklarla ele alınır.

🔹 Denklem Çözme Ünitesinin Alt Başlıkları:

1. Birinci Dereceden Bir Bilinmeyenli Denklemler

2. Birinci Dereceden İki Bilinmeyenli Denklem Sistemleri

3. İkinci Dereceden Denklemler ve Kökleri

4. Mutlak Değerli Denklemler

5. Köklü, Üslü ve Orantılı Denklemler

6. Denklem Kurmaya Yönelik Problemler

7. Denklem Sistemleriyle Yorum ve Kesişim Soruları

🎯 AYT’de Denklem Soruları Nasıl Gelir?

• “Denklemi sağlayan x değerleri toplamı kaçtır?”

• “Denklemin köklerinden biri pozitif, diğerinin mutlak değeri şuysa…”

• “Karmaşık bir ifadeyi sadeleyerek bilinmeyeni bulunuz.”

• “Denklem sisteminin çözüm kümesi nedir?”

• “Denklem kökü bir geometrik/analitik soruda nerede kesişir?”

🎓 Basit Hatırlatma Örneği:

Soru:
denkleminde x kaçtır?

Çözüm:
​

Bu çok temel bir örnek, AYT’de bunun çok daha kapsamlı hâlleri karşımıza çıkar.

Birinci Dereceden Bir Bilinmeyenli Denklemler

📘 Tanım:

Bir bilinmeyeni ve bu bilinmeyenin üstü 1 olan denklemlere birinci dereceden bir bilinmeyenli denklem denir.

Genel biçimi:

ax + b = 0 (a ≠ 0)

Bu tür denklemlerin tek bir çözümü (kökü) vardır ve çözüm:

​

🎯 AYT’de Bu Konu Nasıl Sorulur?

• Temel görünümlü ama çok adımlı işlemler içeren denklemler

• Parantezli, paydalı veya kesirli ifadelerle kurulu denklemler

• Denklem kurma içeren problemler

• Denklemin çözüm kümesini yorumlatan sorular

🎓 Temel Örnekler:

Örnek 1:

Örnek 2 (Parantezli):

Örnek 3 (Kesirli):

​

📌 Paydaları eşitleyip çöz:

Örnek 4 (Sıfır Eşitliği):

📌 İpuçları ve Stratejiler:

• Denklem çözmeden önce parantezleri aç, sadeleştir, payda eşitle

• İşaret hatası → en yaygın tuzaktır

• Çözüm kümesi isteniyorsa: “boş küme” veya “R” olabilir

• Her iki tarafı eşit derecede etkileyen işlemler yapılmalı

• Paydalarda x varsa tanım kümesi ayrıca kontrol edilmeli

​

Mini Alıştırma:

Aşağıdaki denklemleri çözünüz:

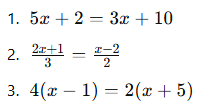
✅ Cevaplar:

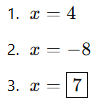
Birinci Dereceden İki Bilinmeyenli Denklem Sistemleri

📘 Tanım:

İki bilinmeyenli (genellikle x ve y) iki denklemin bir araya gelerek oluşturduğu sistemlere iki bilinmeyenli denklem sistemleri denir.

Genel biçim:

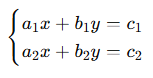
📌 Çözüm Yöntemleri:

1. Yerine Koyma (Substitüsyon)

2. Taraf Tarafa Toplama/Çıkarma (Eliminasyon)

3. Grafik Yöntemi (ayt’de çok sorulmaz)

🎓 1. Yerine Koyma Yöntemi

Bir denklemden bir bilineni yalnız bırakıp, diğerine yerine yazma yöntemidir.

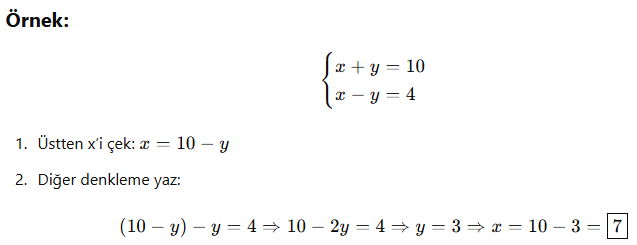
🎓 2. Taraf Tarafa Yöntemi

İki denklemi alt alta yazıp taraf tarafa toplar veya çıkarırız.

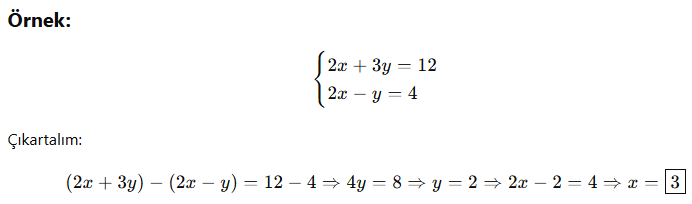
❗ Özel Durumlar:

• Çakışık Doğrular: Sonsuz çözüm ⇒ her denklem birbirinin katı

• Paralel Doğrular: Çözüm kümesi boş ⇒ oranlar eşit, sabitler farklı

• Kesim Noktası: Tek çözüm ⇒ doğrular farklı ve kesişiyor

Mini Alıştırma:

Aşağıdaki sistemleri çözünüz:

✅ Cevaplar:

AYT’de Dikkat Edilecekler:

• Kesirli denklemlerde payda eşitlemeyi unutma

• Mutlak değerli sistemlerde her durumu ayrı ayrı incele

• Bazı sorular sözlü verilip denklem sistemine dökülür

• Denklemlerin oranı = sabit oranı kontrolü sorulabilir (sonsuz/çakışık çözüm)

İkinci Dereceden Denklemler ve Kökleri

📘 Tanım:

Genel formu:

Bu tip denklemlere ikinci dereceden bir bilinmeyenli denklem denir.
Çözümünde genellikle kök bulma formülü kullanılır:

​​

Burada:

🎓 Örnek 1 (İki farklı kök):

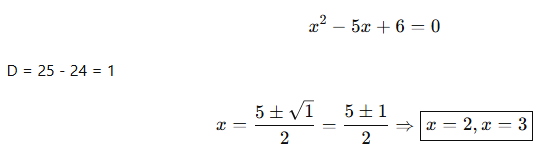
🎓 Örnek 2 (Çift katlı kök):

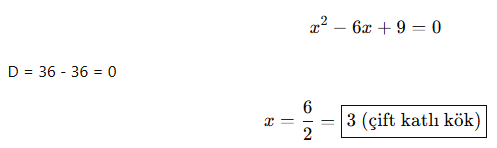
🎓 Örnek 3 (Gerçek kök yok):

D = 1 – 4 = –3
❌ Gerçek sayı çözüm kümesi yok. Çözüm karmaşık sayı olur.

📌 Kökler ve Katsayılar Arasındaki İlişki (Vieta Formülleri):

Eğer denklemin kökleri x1 ve x2​ ise:

Mini Alıştırma:

Aşağıdaki denklemleri çözünüz:

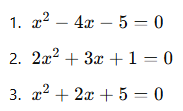
✅ Cevaplar:

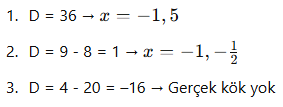
AYT’de Dikkat Edilecekler:

• Kök sayısı soruluyorsa hemen D hesapla

• Köklerden biri belli ise Vieta ile diğerini bul

• Denklemler, grafik yorumları veya parabol sorularında karşına çıkar

• Bazı sorular köklerin çarpımı, toplamı üzerinden çözülür

Mutlak Değerli Denklemler

📘 Tanım:

Mutlak değer, bir sayının 0’a olan uzaklığını ifade eder.
Yani negatif bir ifade bile olsa pozitif olarak düşünülür.

Matematiksel olarak:

AYT’de Mutlak Değerli Denklem Soruları:

• Genellikle eşitliğin iki tarafında da mutlak değer olur

• Sayısal ya da cebirsel mutlak ifadelerin çözümü istenir

• Bazen grafik ya da yorumla birlikte verilir

• Denklemin her durumu ayrı ayrı ele alınarak çözülmelidir

📌 Temel Strateji:

Bir mutlak değerli ifade çözülürken:

1. İçeriği sıfıra eşitleyerek kritik nokta bulunur

2. Sayı doğrusu üzerinde bu noktaya göre parça parça inceleme yapılır

3. Her durumda denklem ayrı ayrı yazılır

4. Bulunan çözüm, mutlak değerli ifadenin tanım koşuluna uygun mu diye kontrol edilir

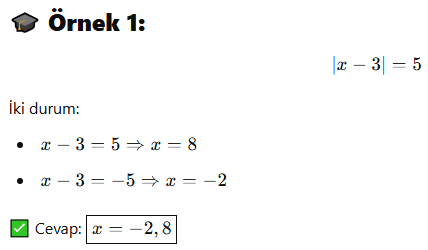
❗ Dikkat:

• Eşitliğin sağ tarafı negatifse çözüm YOKTUR!

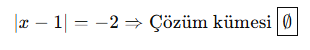
Mini Alıştırmalar:

Aşağıdaki denklemleri çözünüz:

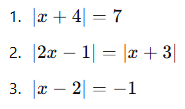
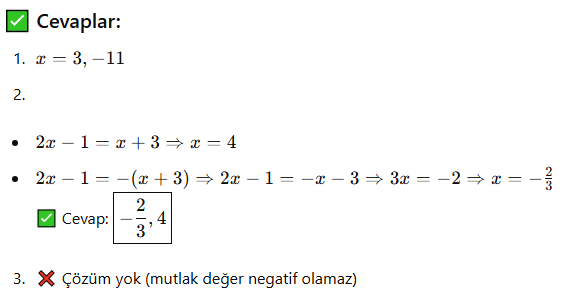
AYT’de Dikkat Edilecekler:

• Her durum ayrı ayrı çözülmeli

• Çözüm sonunda koşulları kontrol etmeyi unutma!

• Özellikle eşitsizliklerde işaret tablosu ile birlikte incelenir

• Sorular genellikle dikkat ve işlem hatasına oynar

Köklü, Üslü ve Orantılı Denklemler

📘 Bu başlık neyi kapsar?

Bu bölümde denklemler artık sadece x değil, x’in kökü, üssü ya da kesirli hâli şeklinde karşımıza çıkar. AYT’de hem işlem hızını hem de dönüşüm bilgini ölçer.

🔹 A. Köklü Denklemler

Köklü denklemler çözülürken genellikle her iki tarafın karesi alınır, ama önce yalnız bırakma yapılır.

🎓 Örnek 1:

🎓 Örnek 2:

❗ Uyarı: Kare alma sonrası sahte kök çıkabilir. Mutlaka denklemde kontrol et!

🔹 B. Üslü Denklemler

Temel mantık:

• Tabanlar aynıysa üstler eşitlenir

• Üstleri eşitlemek için logaritma ya da üs kuralları kullanılabilir

🎓 Örnek 3:

🎓 Örnek 4:

🔹 C. Orantılı (Rasyonel) Denklemler

Payda içeren denklemlerde:

1. Tanımsızlık kontrol edilir (payda ≠ 0)

2. Paydalar eşitlenerek sadeleştirilir

3. Çözümden sonra tanım dışı kalan x değerleri atılır

🎓 Örnek 5:

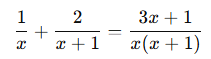
Paydalar eşit → paylar eşitlenir:

Mini Alıştırmalar:

Aşağıdaki denklemleri çözünüz:

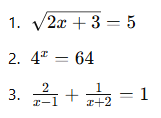
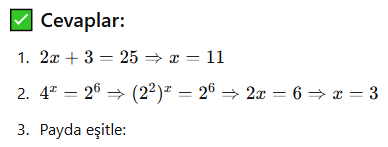
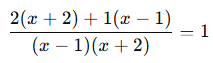
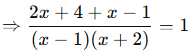
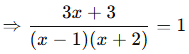
Bu denklem çözülerek kökler bulunur (gerekirse diskriminantla).

AYT’de Dikkat Edilecekler:

• Köklü denklemde sonuç negatifse çözüm kümesi boş olabilir

• Üslü denklemlerde tabanı eşitlemek çözüm hızını artırır

• Rasyonel denklemlerde tanım kümesine dikkat!

• Bu denklemler genellikle karışık sistemlerde de karşımıza çıkar

Denklem Kurmaya Yönelik Problemler

📘 Bu Başlık Ne Anlatır?

Verilen bir metin ya da hikâyeden, doğru denklem kurmak ve çözmek bu başlığın özüdür.
Özellikle:

• Sayı problemleri

• Yaş problemleri

• İşçi – iş – süre problemleri

• Hız – zaman – yol problemleri

• Oran – orantı içeren durumlar

• Parasal işlemler
  gibi konularda denklem kurmak bu başlığın temelidir.

🎯 AYT’de Nasıl Sorulur?

• “Bir sayının 3 fazlasının yarısı, diğer sayının 2 katına eşittir…”

• “Bir baba ile oğlunun yaşları toplamı 60’tır. 4 yıl önce…”

• “Bir işçi 12 günde bitiriyor, ikinci işçi tek başına kaç günde bitirir?”

• “Günde 40 TL harcayan biri 3 gün sonra…”

🎓 Örnek 1 – Sayı Problemi:

Bir sayının 4 eksiğinin 3 katı, 18’e eşittir. Bu sayı kaçtır?

Çözüm:

🎓 Örnek 2 – Yaş Problemi:

Bir babanın yaşı, oğlunun yaşının 4 katıdır. 5 yıl sonra baba 40 yaşında olacak.
Oğul şu an kaç yaşındadır?

Çözüm:

🎓 Örnek 3 – İş Problemi:

Bir işi A işçisi 12 günde, B işçisi 8 günde yapıyor.
İkisi birlikte bu işi kaç günde bitirir?

Çözüm:

🎓 Örnek 4 – Hız Problemi:

Bir araç A noktasından B noktasına saatte 60 km hızla 3 saatte gidiyor.
Geri dönüşte trafik olduğu için 40 km/s hızla dönüyor.
Gidiş – dönüş ortalama hızı kaçtır?

Çözüm:

Toplam yol = 60 × 3 = 180 km
Dönüş: 180 ÷ 40 = 4.5 saat
Toplam yol = 360 km, toplam süre = 7.5 saat

📌 İpuçları:

• Metni okurken bilinmeyeni x olarak tanımla

• Tüm verileri denklemle ifade et

• Zaman, oran, yaş, hız, karışım gibi kavramları hemen yerine yerleştir

• Denklemi sadeleştirip çözdükten sonra mantıksal kontrol yap

• AYT sorularında gerçek yaşam bağlamı genellikle dikkati ölçmek içindir

Mini Alıştırmalar:

1. Bir sayının 3 katı ile 7 fazlası, 28 eder. Sayı kaçtır?

2. Bir işçi günde 8 saat çalışarak bir işi 15 günde tamamlıyor. Aynı işi 10 saat çalışan bir işçi kaç günde bitirir?

3. İki sayının farkı 12, toplamları 48 ise büyük sayı kaçtır?

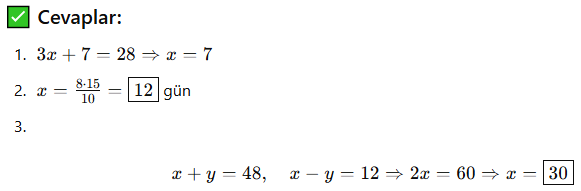
Denklem Sistemlerinde Grafik ve Kesişim Yorumları

📘 Bu Başlık Ne İşler?

İki denklem (genellikle doğrular) bir sistem oluşturduğunda, bu sistemin çözümü aynı zamanda doğruların kesişim noktasıdır.
AYT’de grafiksel yorum soruları da bu mantık üzerine kuruludur.

🔹 Durumlar:

​​

Bu iki doğrunun grafiksel ilişkisi:

🎓 Örnek 1: Kesişen Doğrular

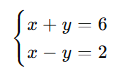
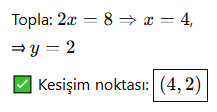
🎓 Örnek 2: Paralel Doğrular

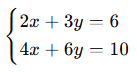
Oranlar:

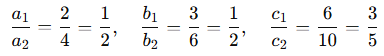
⇒ Katsayı oranları aynı, sabit terim oranı farklı ⇒ Paralel
✅ Çözüm kümesi: ∅​

🎓 Örnek 3: Çakışık Doğrular

​

İkinci denklem birincinin 2 katı → aynı doğru
✅ Çözüm kümesi: ​

📌 Grafiksel Bilgi:

• Denklem sistemlerinin çözüm noktası, grafik üzerinde kesişim noktasıdır

• Bu nokta hem x hem y için iki denklemi sağlayan ortak noktadır

• Eğer kesişim noktası yoksa, sistemin çözümü de yoktur

• Özellikle mutlak değerli veya parabolik denklem sistemlerinde, grafik yorumlama önemlidir

Mini Alıştırmalar:

🧠 AYT’de Dikkat Edilecekler:

• Denklem sistemleri geometri sorularının içinde gizli olabilir

• Grafik çizilmeden sadece oranlara bakarak yorum yapılabilir

• “Bu sistemin çözüm kümesi nedir?” → sadece işlem değil, ilişkiyi görme sorusudur

• Mutlak değer, parabol, çember gibi farklı grafiklerde de “kesişim noktası” sorulabilir

AYT Denklem Çözme 10 Soruluk Deneme Testi

Her soru farklı bir alt başlıktan geliyor ve AYT seviyesindedir.
Cevap anahtarı en altta.