AYT Matematik Diziler Konu Anlatımı

Diziler, belirli bir kurala göre sıralanmış sayılar topluluğudur.
Her eleman bir sıraya sahiptir ve genellikle:

a1, a2, a3,…, an​

şeklinde gösterilir.

AYT’de diziler konusu;

• Genel terim bulma

• Aritmetik ve geometrik dizi özellikleri

• Özdeşlikler, denklem kurma

• Dizi kuralları ile problem çözme
  üzerine kurulur.

🔹 Ünitenin Alt Başlıkları:

1. Dizi Kavramı ve Gösterimi

2. Aritmetik Dizi

3. Geometrik Dizi

4. Genel Terim ve Rekürsif Tanım

5. Dizi Problemleri ve Uygulamalar

Dizi Kavramı ve Gösterimi

📘 A. Dizi Nedir?

Dizi, belli bir kurala göre sıralanmış sonlu ya da sonsuz sayı topluluğudur.
Her sayıya terim, her terimin sırasına indis denir.

📘 B. Gösterim Şekli

Bir dizinin terimleri:

şeklinde gösterilir.

🎓 Örnek 1:

Bu, her terimi bir öncekinden 3 fazla olan bir dizidir.

📘 C. Dizi Türleri

• Sabit Dizi: Her terim aynı (örneğin: 5, 5, 5, 5, …)

• Doğrusal (Aritmetik) Dizi: Terimler arasında sabit fark var

• Üstel (Geometrik) Dizi: Terimler arasında sabit oran var

• Kurallı Dizi: Belirli bir matematiksel formülle tanımlanmış

• Rekürsif Dizi: Her terim, önceki terim(ler) kullanılarak tanımlanmış

📘 D. Dizi ve Fonksiyon Arasındaki Fark

Aritmetik Dizi

📘 A. Tanım

Bir dizide, ardışık iki terim arasındaki fark sabit ise bu diziye aritmetik dizi denir.

Bu sabit farka:

​

denir.

📘 B. Aritmetik Dizi Formülleri

🔹 Genel Terim (n. terim):

​

🔹 İki Terim Arasındaki Terim:

🔹 Toplam Formülü:

İlk n terimin toplamı:

📘 C. Ortadaki Terim Özelliği

Aritmetik dizide:

​​​

Ortadaki terim, etrafındaki iki terimin aritmetik ortalamasıdır.

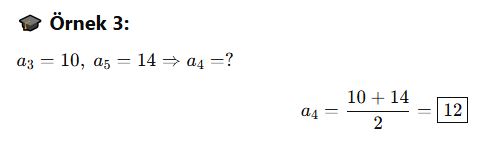
Geometrik Dizi

📘 A. Tanım

Ardışık terimleri arasında sabit bir oran bulunan dizilere geometrik dizi denir.

Bu sabit orana:

​

denir.

📘 B. Geometrik Dizi Formülleri

🔹 Genel Terim:

🔹 İki Terim Arasındaki Terim:

🔹 İlk n Terimin Toplamı (r ≠ 1):

📘 C. Ortadaki Terim Özelliği

Geometrik dizide:

​​

Ortadaki terimin karesi, etrafındaki iki terimin çarpımına eşittir.

Genel Terim ve Rekürsif Tanım

📘 A. Genel Terim Nedir?

Bir dizinin her terimini n’e bağlı olarak veren formüle genel terim denir:

​

Bu formül sayesinde istenilen terim kolayca bulunur.

🎓 Örnek 1:

Bu bir aritmetik dizidir.

📘 B. Rekürsif (Özyinelemeli) Tanım

Bir dizinin her teriminin önceki terime bağlı olarak tanımlanmasıdır:

​

Yani bir sonraki terim, bir önceki terime göre hesaplanır.

📘 C. Genel Terim Bulma (Rekürsif → Direkt)

🎓 Örnek 4:

Verilen:

Bu bir aritmetik dizi ⇒

🎓 Örnek 5 (Karışık Dizi):

Verilen:

Negatif–pozitif dönüşümlü bir dizidir.

Dizi Problemleri ve Uygulamalar

📘 A. Dizi ile Denklem Kurma

Bazı sorularda dizinin genel terimi verilmez ama bazı terimleriyle denklem kurmamız gerekir.

🎓 Örnek 1:

Bir dizinin 3. terimi 10, 6. terimi 19’dur. Dizi aritmetik olduğuna göre genel terimi nedir?

Bu iki denklemden:

📘 B. Terimler Toplamı ile Kurgu Soruları

Bazı problemler toplam formülüyle çözülür.

🎓 Örnek 2:

Bir öğrenci her gün 2 TL fazla para biriktiriyor. İlk gün 1 TL koyduğuna göre, 10 günde toplam kaç TL biriktirmiştir?

Bu bir aritmetik dizi:

📘 C. Eşitlik Kurmalı Sorular (Kesişim, Denk Olanlar)

🎓 Örnek 3:

📘 D. Karışık Dizi Problemleri (Modelli – Kelimeli)

Bu tür sorularda dizi doğrudan verilmez, senaryoyla tanımlanır.
→ Genel terimi ya da toplamı bulmak gerekir.

🎓 Örnek 4:

Bir şirketin ilk ay geliri 10 bin TL’dir. Her ay bir öncekinin 1.2 katı kadar gelir elde ediliyor.
→ 4. ay geliri ne olur?

Bu bir geometrik dizi:

Diziler AYT Deneme Testi

(Cevap anahtarı en altta)