AYT Matematik İntegral Konu Anlatımı

İntegral, türevin tersi olarak düşünülebilir.
Bir fonksiyonun altında kalan alanı, toplam değişimi veya birikimi ölçmeye yarar.

AYT’de integral konusu;

• Belirsiz integral (türev alma işleminin tersi)

• Belirli integral (alan, net değişim)

• Alan hesaplamaları

• İntegral alma kuralları

• Grafik ve uygulamalı problem çözümleri

gibi başlıklardan oluşur.

🔹 Ünitenin Alt Başlıkları:

1. Belirsiz İntegral Kavramı ve Temel Kurallar

2. İntegral Alma Teknikleri (Polinom, köklü, rasyonel)

3. Belirli İntegral ve Alan Hesaplama

4. Fonksiyonlar Arası Alan

5. Grafikle İntegral Yorumu

6. Uygulamalı Problem Çözümü (Alan, hacim, toplam değişim)

Belirsiz İntegral Kavramı ve Temel Kurallar

📘 A. Belirsiz İntegral Nedir?

Türev alma işleminin tersidir.
Bir fonksiyonun türevini alarak nasıl türevi elde ediyorsak, türevden geriye gitmek için integral alınır.

📘 B. Temel İntegral Kuralları

📘 C. Sabit Çarpan ve Toplam Kuralı

📘 1. Sabit Çarpan Kuralı:

Bir sabit sayı integralin dışına çarpan olarak çıkarılabilir:

📘 2. Toplama ve Çıkarma Kuralı:

İki fonksiyonun toplamının integrali, ayrı ayrı integral alınıp toplanabilir:

📘 D. İntegralin Türevle Kontrolü

Bir ifadenin integralini alıp, sonra türevini alırsanız başlangıç fonksiyonuna geri dönersiniz.

🎓 Örnek 3:

İntegral Alma Teknikleri (Polinom, Köklü, Rasyonel)

📘 A. Polinomların İntegrali

📘 Genel Kural:

Eğer elimizde bir polinom varsa:

​

Bu tür fonksiyonların integrali terim terim alınır:

🎓 Örnek:

🎓 Örnek:

🎓 Örnek:

📘 B. Köklü İfadelerin İntegrali

Köklü ifadeleri üs olarak yazmak işimizi kolaylaştırır:

🎓 Örnek:

📘 C. Rasyonel İfadelerin İntegrali

İki durum vardır:

1. Pay, paydanın türevidir:

🎓 Örnek:

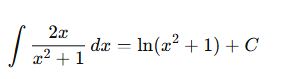
2. Standart üs kullanımı:

📘 D. Parçalama (Terimlere Ayırma)

📘 E. İntegral + Sabit Dönüşüm Kullanımı

Belirli İntegral ve Alan Hesaplama

📘 A. Belirli İntegral Nedir?

Belirli integral, bir fonksiyonun [a, b] aralığında altında kalan alanı ya da toplam değişimini bulur.

​

Burada F(x), f(x)‘in bir integralidir (yani asal fonksiyonu).

📘 B. Geometrik Yorum

• Eğrinin x-ekseniyle arasında kalan net alanı verir

• Eğer grafik x-ekseni altında kalıyorsa, o kısımdaki integral negatif olur

📘 C. Alan Hesaplama (Mutlak Değerli)

Bir alan sorusunda grafik eksenin altındaysa, çıkan negatif değerin mutlak değeri alınır.

🎓 Örnek 2:

​

Alan sorusuysa: |–4| = 4 birim²

📘 D. Belirli İntegralin Özellikleri

Mini Alıştırmalar:

Fonksiyonlar Arasındaki Alan Hesaplama

📘 A. İki Fonksiyon Arasındaki Alan

İki fonksiyonun sınırladığı bölgede kalan alan:

​

• f(x): Üstte kalan (büyük olan) fonksiyon

• g(x): Altta kalan (küçük olan) fonksiyon

• Sınırlar: x=a  ile x=b arası

📘 B. Grafiğe Göre Alan Hesabı

• Önce kesişim noktaları bulunur: f(x)=g(x) çözülür

• Alan parçalar hâlindeyse ayrı ayrı integral alınır

• Fonksiyonların birbirini geçtiği durumlarda mutlak değerle düşünülür

📘 C. Mutlak Değerli Durumlar

Eğer fonksiyonlar bir noktada yer değiştiriyorsa:

• Her parça için ayrı integral alınır

• Alan negatif çıkarsa mutlak değer alınır

Mini Alıştırmalar:

Grafikle İntegral Yorumu

📘 A. İntegral Grafik Üzerinde Neyi Gösterir?

• Bir fonksiyonun grafiği ile x-ekseni arasında kalan alansal büyüklüğü gösterir.

• Pozitif alan: Grafik x-ekseni üstünde

• Negatif alan: Grafik x-ekseni altında

📘 B. Alan Toplamı ve Mutlak Değer

Alan sorularında:

​​

• Negatif bölgelerde mutlak değer alınır

• Toplam alan ≠ net alan

📘 C. Grafikten Tahmini İntegral Değeri

• Alan büyüklüğü geometrik şekillerden çıkarılabilir:

  • Dikdörtgen, üçgen, yamuk

  • Pozitif/negatif alanlar dikkatli ayrılır

• Grafikteki simetri özellikleri (örneğin, tek/çift fonksiyonlar) kullanılabilir

🎓 Örnek 2:

Grafikte f(x), x-ekseni altında ve üçgen biçimindedir:

• Taban: 2 birim, Yükseklik: 4 birim

​

(Çünkü grafik eksen altında)

📘 D. Eksen Altı – Üstü Ayırımı

Mini Alıştırmalar (Grafiksiz sayısal)

Uygulamalı Problem Çözümü (Alan, Hacim, Toplam Değişim)

📘 A. İntegralin Uygulama Alanları

İntegral, yalnızca grafik alanı değil:

• Hızdan yer bulma

• Akışkanlık, birikim, değişim

• Alan – hacim hesaplama

• Ekonomi: kâr – maliyet – gelir

• Geometri: dönel cisim hacmi (ileri seviye)

gibi pek çok alanda kullanılır.

📘 B. Hız – Yer İlişkisi (Fiziksel Uygulama)

📘 C. Birikim ve Net Değişim

📘 D. Alan/Hacim Problemleri

Alanlar zaten önceki başlıkta işlendi.
Hacim hesaplamaları genelde ileri seviye ve ÖSYM dışı olsa da şu tip gelir:

🎓 Örnek 3:

Mini Alıştırmalar:

İntegral AYT Deneme Testi

(Cevap anahtarı en altta)