AYT Matematik İstatistik Konu Anlatımı

İstatistik, verilerin:

• Toplanması

• Sınıflandırılması

• Özetlenmesi

• Yorumlanması
  süreçlerini kapsayan bir matematik dalıdır.

AYT’de bu ünitede özellikle:

• Aritmetik ortalama

• Medyan (ortanca)

• Mod (tepe değer)

• Standart sapma

• Varyans

• Grup verilerde analiz

• Boxplot (kutu grafiği) yorumları
  gibi başlıklar üzerinde durulur.

🔹 Ünitenin Alt Başlıkları:

1. Veri ve Frekans Kavramı

2. Aritmetik Ortalama

3. Mod ve Medyan

4. Varyans ve Standart Sapma

5. Gruplandırılmış Veriler

6. Grafikler ve Yorumlar

7. Uygulamalı İstatistik Soruları

🎯 AYT’de Nasıl Sorulur?

• Sayısal verilerden ortalama, medyan, mod veya standart sapma istenir

• Tablo veya grafik yorumları

• Bir grubun özelliği bilindiğinde tüm grup hakkında çıkarım yapılır

• Ağırlıklı ortalama, veri güncelleme problemleri

Veri ve Frekans Kavramı

📘 A. Veri Nedir?

Veri, ölçme, sayma ya da gözlem yoluyla elde edilen bilgiler bütünüdür.

Örnek:
Bir sınıftaki öğrencilerin yaşları, bir fabrikanın günlük üretim miktarları, bir sınavdaki doğru cevap sayıları…

📘 B. Nitel ve Nicel Veri

📘 C. Frekans (Sıklık) Nedir?

Bir verinin kaç kez tekrar ettiğini gösterir.

Örnek:
Veri kümesi: [2, 3, 3, 5, 5, 5, 6]
→ 5 sayısının frekansı = 3

📘 D. Frekans Tablosu

Verilerin tekrarlanma sayısını tablo hâlinde gösterir.

🎓 Örnek:

Bir sınavda öğrencilerin aldıkları puanlar:
[60, 70, 70, 80, 90, 90, 90, 100]

→ Frekans tablosu:

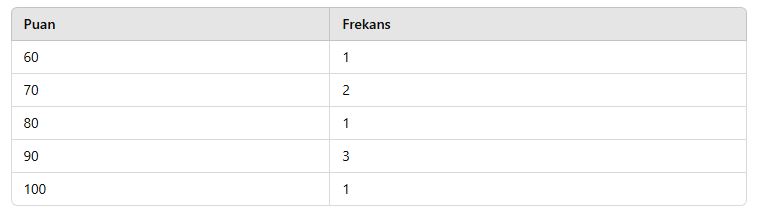
📌 Not:

Frekansların toplamı, toplam veri sayısını verir.

Mini Alıştırmalar:

1. Veri kümesi: [4, 5, 5, 6, 7, 7, 7, 7]
    → 7’nin frekansı kaçtır?

2. Veri kümesinde toplam 10 sayı var. “8” sayısı 4 kez geçiyor.
    → 8’in frekansı nedir?

3. Aşağıdaki veri kümesinin frekans tablosunu oluştur:
   [3, 3, 4, 4, 4, 5, 6, 6]

✅ Cevaplar:

1. 4

2. 4

3. Frekans tablosu:

Aritmetik Ortalama

📘 Aritmetik Ortalama Nedir?

Bir veri grubundaki sayıların toplamının, veri sayısına bölünmesiyle elde edilen değerdir.

​​

🎓 Örnek 1:

Sayılar: 5, 7, 8, 10, 10

​

📘 Ağırlıklı Aritmetik Ortalama

Her verinin farklı önemi/frekansı varsa, ağırlıklı ortalama kullanılır.

🎓 Örnek 2:

Bir öğrencinin notları ve katsayıları:

📘 Veri Güncellenirse Ortalama

Bir veri eklenirse veya çıkarılırsa yeni ortalama şu şekilde bulunur:

🎓 Örnek 3:

5 öğrencinin ortalaması 70 → toplam: 350
Yeni gelen öğrencinin notu: 80

Mini Alıştırmalar:

1. [6, 7, 8, 9, 10] → Ortalama?

2. Ağırlıklı ortalama:
    Notlar: 100 (2 kez), 80 (3 kez), 60 (1 kez)

3. Ortalama 75 olan 4 verinin toplamı?
    Sonradan 90 eklendiğinde yeni ortalama?

Mod ve Medyan

📘 A. Mod (Tepe Değer)

Bir veri grubunda en çok tekrar eden değerdir.

Aynı frekansta birden fazla değer varsa → birden çok mod vardır
Tüm değerler farklıysa → mod yoktur

🎓 Örnek 1:

Veri: [4, 5, 5, 6, 7, 7, 7, 8]
→ En çok tekrar eden: 7

🎓 Örnek 2:

Veri: [2, 3, 3, 5, 5, 6]
→ 3 ve 5, aynı sayıda tekrar etmiş

📘 B. Medyan (Ortanca Değer)

Veriler küçükten büyüğe sıralanır.

• Tek sayıda veri varsa:
   ortadaki tek değer

• Çift sayıda veri varsa:
   ortadaki iki değerin aritmetik ortalaması

🎓 Örnek 3:

Veri: [3, 4, 6, 7, 8]
→ Ortadaki: 6

🎓 Örnek 4:

Veri: [1, 2, 4, 6, 7, 9]
→ Ortadaki iki sayı: 4 ve 6

📌 Not:

• Mod: En çok tekrar

• Medyan: Ortadaki değer

• Aritmetik ortalama ile karıştırılmamalı

Mini Alıştırmalar:

1. Veri kümesi: [2, 4, 4, 5, 6, 7, 7, 7, 8]
   → Mod ve medyan?

2. [10, 20, 30, 40, 50] için medyan?

3. [6, 7, 8, 9, 9, 9, 10] için mod?

✅ Cevaplar:

1. Mod = 7, Medyan = 6

2. Ortadaki: 30 → Medyan = 30

3. Mod = 9

Varyans ve Standart Sapma

📘 A. Varyans Nedir?

Varyans, verilerin ortalamaya göre ne kadar sapma gösterdiğini ölçer.
→ Sapmaların karesinin ortalamasıdır.

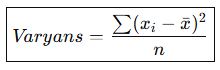
📘 B. Standart Sapma Nedir?

Standart sapma, varyansın kareköküdür.
→ Verilerin ortalama etrafında dağılım miktarını gösterir.

​​

📘 C. Pratik Formül (Gerekirse):

📌 Notlar:

• Tüm veriler aynıysa → sapma = 0

• Sapmalar pozitif olduğu için kare alınır

• Standart sapma her zaman pozitiftir

Mini Alıştırmalar:

1. Veriler: [5, 5, 5, 5] → Varyans ve sapma?

2. Veriler: [3, 6, 9]
    → Ortalama? Varyans? Standart sapma?

Gruplandırılmış Verilerde İstatistik

📘 Gruplandırılmış Veri Nedir?

Veriler çok fazla ve yoğun olduğunda, belirli aralıklara (sınıflara) bölünerek gösterilir.
Her sınıfın bir frekansı (kaç tane veri içerdiği) ve bir sınıf ortası (sınıf değeri) olur.

🧠 Terimler:

📘 Aritmetik Ortalama (Gruplu):

🎓 Örnek:

Bir sınavda öğrencilerin puanları şu şekilde verilmiştir:

Adım 1: Sınıf Ortalarını Bul

📘 Not:

• Gruplandırılmış verilerde tek tek veri bilinmez, bu yüzden ortalamalar yaklaşık değer olur.

• Aynı yöntemle mod, medyan ve standart sapma da yaklaşık olarak hesaplanabilir (AYT’de genelde aritmetik ortalama istenir).

Mini Alıştırmalar:

Bir veri grubu aşağıdaki gibi verilmiştir:

1. Sınıf ortalarını yazınız

2. Aritmetik ortalamayı bulunuz

✅ Cevaplar:

Grafikler ve Yorumlar

📘 A. Histogram

• Sınıf aralıklarına göre çizilir

• Sınıf ortaları yatay eksende, frekanslar dikey eksende gösterilir

• Sütunlar bitişik çizilir

• Alan → veri miktarını temsil eder

🔹 Sıklıkla grup veri sorularında kullanılır
🔹 Yükseklik değil, alan karşılaştırması önemlidir

🎓 Örnek Histogram Yorumu:

→ En çok veri hangi aralıkta? → 20–30
→ Verilerin dağılımı hangi yönde? (Simetrik, sola/sağa yatık?)
→ Ortalama yaklaşık hangi değerde?

📘 B. Çubuk Grafik

• Nitel ya da nicel ayrık veriler için uygundur

• Kategoriler yatay eksende, frekanslar dikey eksende

• Sütunlar ayrı çizilir

• Yorum: En çok hangi kategori? Farklar nedir?

🎓 Örnek:

Bir sınıfta öğrencilerin tuttukları takımlar:

→ En çok tercih edilen: B
→ C ile B arasında fark: 7 kişi
→ Grafik ayrık veriyi gösterir

📘 C. Kutu Grafiği (Boxplot)

• Verinin 5 sayı özeti kullanılır:

  • En küçük değer

  • 1. çeyrek (Q1)

  • Medyan (Q2)

  • 3. çeyrek (Q3)

  • En büyük değer

• Veri setinin dağılımını görsel olarak özetler

• Aykırı değer olup olmadığı görülebilir

🎓 Örnek Yorumlar:

• Kutu simetrikse → veri dağılımı simetrik olabilir

• Kutu sola kısa → veri sağa yatık

• Medyan Q1’e yakın → alt veriler yoğun

• Aykırı veri varsa → grafikte ayrı gösterilir (noktacık)

Mini Alıştırmalar:

1. Histogramda en yüksek sütun = 15 kişi → bu aralık ne anlama gelir?

2. Bir kutu grafiğinde medyan Q3’e daha yakınsa ne söylenebilir?

3. Çubuk grafikte bir kategori hiç yoksa, o neyle gösterilir?

✅ Cevaplar:

1. O aralıkta 15 kişi vardır → en yoğun sınıf

2. Alt veriler daha yaygındır, dağılım sağa yatık olabilir

3. Frekansı 0 olan kategori → sütun çizilmez

Uygulamalı İstatistik Soruları

📘 Bu Başlıkta Neler Var?

• Aritmetik ortalama, mod, medyan, standart sapma bir arada

• Veri eklenirse/çıkarılırsa yeni ortalama

• Grup verilerde yorum

• Grafik yorumları

• Kutu grafiği ile tahmin ve kıyaslama

• Gerçek AYT tarzı karışık sorular

🎓 Örnek 1: Ortalama Güncelleme

Bir sınıfta 5 öğrencinin sınav ortalaması 60’tır.
Sınıfa yeni katılan öğrencinin notu 90’dır.
Yeni ortalama kaç olur?

Toplam: 5 × 60 = 300
Yeni toplam: 300 + 90 = 390
Yeni öğrenci sayısı: 6

🎓 Örnek 2: Kutu Grafiği Yorumu

Bir veri setinin 5 sayı özeti:
Min = 10, Q1 = 20, Medyan = 25, Q3 = 30, Max = 50

→ Aykırı değer var mı?
→ Veri sağa mı sola mı yatık?

Q3–Q1 = 10 → IQR
Max – Q3 = 20, Min – Q1 = –10
→ Sağ tarafa yatık, 50 aykırı olabilir

🎓 Örnek 3: Ağırlıklı Ortalama – Bölüm Notu

Bir öğrencinin sınavları:

• Vize (40%) → 60

• Final (60%) → 80

📘 İstatistiksel Yorum Sorusu:

Veri: [20, 30, 30, 40, 50, 60, 70]

→ Mod: 30
→ Medyan: 40
→ Ortalama > medyan > mod → veri sağa yatık

Mini Alıştırmalar:

1. 4 öğrencinin ortalaması 70’tir. Yeni bir öğrenci geldi, yeni ortalama 72 oldu. Bu öğrencinin notu kaç?

2. Bir kutu grafiğinde medyan Q1’e çok yakın, Q3 uzak. Dağılım ne yöndedir?

3. Vize (30%) = 50, Final (70%) = 80 → bölüm notu?

✅ Cevaplar:

1. 4 × 70 = 280 → yeni toplam = 72 × 5 = 360 → yeni öğrenci = 360 – 280 = 80

2. Q1–Medyan küçük, Medyan–Q3 büyük → veri sağa yatık

AYT İstatistik Testi

Cevap anahtarı en altta
Her soru farklı bir alt başlıktan seçilmiştir

1. (Veri ve Frekans)

Veri kümesi: [3, 5, 5, 7, 7, 7, 9]
Bu veri kümesinde 7’nin frekansı kaçtır?

A) 1 B) 2 C) 3 D) 4

2. (Aritmetik Ortalama)

[6, 8, 10, 12, 14] sayı grubunun aritmetik ortalaması kaçtır?

A) 10 B) 9 C) 8 D) 12

3. (Ağırlıklı Ortalama)

Bir öğrencinin sınavları:

• Matematik (ağırlık 4): 80

• Fizik (ağırlık 2): 60

• Kimya (ağırlık 3): 70
  Ağırlıklı ortalama nedir?

A) 70 B) 72 C) 73.3 D) 74

4. (Mod – Medyan)

Veri kümesi: [4, 6, 6, 8, 10, 10, 12]
Bu kümenin mod ve medyanı nedir?

A) Mod: 6 – Medyan: 8
B) Mod: 6 – Medyan: 10
C) Mod: 10 – Medyan: 8
D) Mod: 6 ve 10 – Medyan: 8

5. (Varyans)

Veri kümesi: [4, 6, 10]
Aritmetik ortalama kaçtır? Varyansı yaklaşık nedir?

A) Ort: 6.5 – Varyans: 6
B) Ort: 7 – Varyans: 6
C) Ort: 6.5 – Varyans: 7
D) Ort: 6 – Varyans: 5

6. (Standart Sapma)

Veri: [2, 4, 6, 8]
Bu verinin standart sapması yaklaşık kaçtır?

A) 2
B) 2.5
C) 3
D) 1.5

7. (Gruplu Veri)

Aşağıdaki sınıf tablosuna göre ortalama kaçtır?

A) 24
B) 26
C) 28
D) 30

8. (Histogram Yorumu)

Bir histogramda en yüksek sütun 25 kişiyle 40–50 aralığında ise, bu aralık için en doğru yorum hangisidir?

A) Ortalama 45’tir
B) Medyan bu aralıktadır
C) Veri sola yatıktır
D) Bu sınıfın frekansı en azdır

9. (Kutu Grafiği)

Bir veri kümesinin 5 sayı özeti:
Min = 20, Q1 = 30, Medyan = 40, Q3 = 50, Max = 52
Bu verilere göre dağılım için hangisi söylenebilir?

A) Simetriktir
B) Sağa yatıktır
C) Sola yatıktır
D) Aykırı değer yoktur

10. (Ortalama Güncelleme)

Bir grubun ortalaması 60’tır. Toplam 5 kişi vardır.
6. kişinin notu 90 ise, yeni ortalama kaç olur?

A) 65
B) 66
C) 70
D) 75