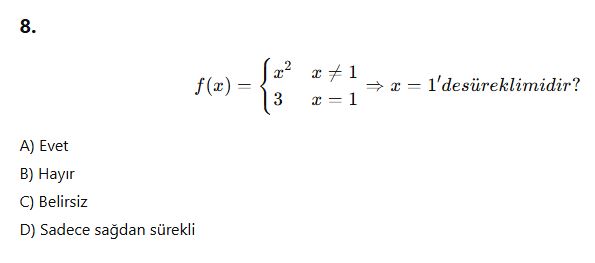AYT Matematik Limit Konu Anlatımı

Limit, bir fonksiyonun belirli bir noktaya yaklaştıkça aldığı değeri incelemeye yarayan temel bir analiz konusudur.

AYT’de limit konusu;

• Soldan ve sağdan limit

• Bir fonksiyonun bir noktadaki limiti

• Sonsuzda limit

• Süreklilik ile ilişkisi

• Limit içeren grafiksel yorumlar

• Belirsizlikler ve sadeleştirme işlemleri

gibi başlıklardan oluşur.

🔹 Ünitenin Alt Başlıkları:

1. Limit Kavramı ve Tanımı

2. Sağdan ve Soldan Limit

3. Bir Noktada Limitin Varlığı

4. Limit Alma Kuralları ve İşlemler

5. Sonsuzda Limit ve Yatay Dikey Asimptot

6. Limit – Süreklilik İlişkisi

7. Belirsizlikler ve Sadeleştirme

Limit Kavramı ve Tanımı

📘 A. Limit Nedir?

Bir fonksiyonun, $x$ değeri belirli bir noktaya yaklaştığında f(x)‘in yaklaştığı değere o fonksiyonun limiti denir.

​

Bu şu anlama gelir:
x, a’ya yaklaşırken f(x), L’ye yaklaşır.

📘 B. Limitin Temel Özelliği

• x=a noktasındaki değer değil, o noktaya yaklaşıldığında ne olduğu önemlidir.

• Fonksiyon o noktada tanımsız bile olabilir, ama limit yine de var olabilir.

🎓 Örnek 1:

📌 Bu tür durumlarda sadeleştirme ile limit bulunabilir.

📘 C. Limitin Grafiksel Anlamı

• Bir fonksiyonun grafiğinde, x→a yaklaşırken
   f(x) değerleri L’ye yaklaşıyorsa,

• Fonksiyon, o noktada tanımlı olmasa da, limitin varlığı mümkündür.

🎓 Örnek 2:

Bir grafik çizilmiş ve x→3 yaklaşırken f(x)→5 gözleniyor.

​

Fonksiyon 3’te tanımsız olsa bile, limit 5 olabilir.

📌 Not:

Limitin var olması için:

• Fonksiyonun sağdan ve soldan limitleri eşit olmalı

• Değer ne çıkarsa çıksın, x → a davranışına bakılır

Sağdan ve Soldan Limit

📘 A. Yönlü Limit Nedir?

Bir fonksiyonun belirli bir noktaya:

• Sağdan (x > a) yaklaşırken limitine sağdan limit,

• Soldan (x < a) yaklaşırken limitine soldan limit denir.

📘 Gösterimi:

• Soldan limit:
  ​

• Sağdan limit:
  

📘 Bir Noktada Limitin Var Olması İçin:

Sağdan ve soldan limitler eşit değilse, o noktada limit yoktur.

🎓 Örnek 1: (Parçalı Fonksiyon)

🎓 Örnek 2: (Limit Yok)

📘 Grafiksel Yorum:

• Sağdan ve soldan değerler farklı seviyelere yaklaşıyorsa limit yoktur

• Aynı seviyeye yaklaşılıyorsa limit vardır

• Nokta açık/kapalı olsa bile bu durumu etkilemez

Bir Noktada Limitin Varlığı

📘 A. Limitin Varlık Koşulu

Bir fonksiyonun $x=a$ noktasındaki limiti var diyebilmek için:

​

olmalıdır.

Yani:

• Sağdan limit = Soldan limit

• Eşit olunan bu değere de limiti denir

📌 Fonksiyon o noktada tanımlı olmak zorunda değildir.
Limit, sadece yaklaşım ile ilgilidir.

📘 B. Tanımlı Olma Zorunluluğu Yoktur

Fonksiyon $x=a$ noktasında tanımsız olsa bile limit var olabilir.

🎓 Örnek 3:

​

Fonksiyon 1’de tanımsız ama limit var.

Limit Alma Kuralları ve İşlemler

📘 A. Temel Limit Kuralları

Eğer

ise:

📘 B. Doğrudan Yerine Yazma

Fonksiyon sürekli ise ve tanımsızlık yoksa,

🎓 Örnek 1:

📘 C. Karmaşık İfadelerde İşlem

Tanımsızlık çıkarsa:

• Sadeleştirme

• Çarpanlara ayırma

• Payda eşitleme

• Rasyonel ifade düzenleme

• Özdeşlik kullanma
  gereklidir.

📘 D. Kök İçeren İfadelerde Eşlenik Kullanımı

🎓 Örnek 4:

​

Eşlenik:

Sonsuzda Limit ve Yatay – Dikey Asimptot

📘 A. Sonsuzda Limit Nedir?

Fonksiyonun  giderken aldığı değeri ifade eder.

​

📘 B. Rasyonel Fonksiyonlarda Sonsuzda Limit

Genel form:

​

Karşılaştırma:

📘 C. Yatay Asimptot Nedir?

Yatay asimptot:

→ Fonksiyon grafiği bu yataya yaklaşır, ama dokunmaz.

🎓 Örnek:

📘 D. Dikey Asimptot Nedir?

Dikey asimptot:

→ Paydanın sıfır olduğu, ama payın sıfır olmadığı yerlerdir.

🎓 Örnek:

Limit – Süreklilik İlişkisi

📘 A. Süreklilik Nedir?

Bir fonksiyon, bir noktada koptuysa, atlama varsa, ya da tanımsızsa, o noktada süreksizdir.
Aksi durumda, o noktada süreklidir.

📘 B. Süreklilik Koşulları (x = a için):

📘 C. Süreksizlik Türleri

📘 D. Süreklilik → Limitin Var Olmasını Zorunlu Kılar

Ancak limitin var olması, fonksiyonun sürekli olduğu anlamına gelmez.

Belirsizlikler ve Sadeleştirme Yöntemleri

📘 A. Belirsizlik Nedir?

Bir limit ifadesi, doğrudan yerine yazıldığında anlamlı bir sonuç vermezse, bu bir belirsizliktir.

📘 B. En Sık Görülen Belirsizlikler:

📘 C. Belirsizlik Nasıl Çözülür?

1. Sadeleştirme

Çarpanlara ayırma – Ortak parantez – Özdeşlik

2. Eşlenik ile çarpma

Köklü ifadelerde kullanılır

3. Payda eşitleme

Çıkarma ya da fark durumlarında

4. Rasyonel ifade düzenleme

Limit AYT Deneme Testi

(Cevap anahtarı en altta)