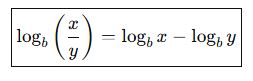AYT Matematik Logaritma Konu Anlatımı

Logaritma, üstel fonksiyonların tersi olarak tanımlanan ve matematikte birçok denklemi çözmemizi kolaylaştıran güçlü bir araçtır.

Bu ünitede:

• Logaritmanın tanımı ve özellikleri

• Logaritmik ifadelerin sadeleştirilmesi

• Logaritma–Üstel ifade dönüşümleri

• Logaritma içeren denklemlerin çözümü

• Farklı tabanlı logaritmalar ve değişim formülü

• Grafikler ve uygulamalı sorular

ön plandadır.

🔹 Ünitenin Alt Başlıkları:

1. Logaritmanın Tanımı ve Üstel Fonksiyonlarla İlişkisi

2. Logaritmanın Temel Özellikleri

3. Logaritmanın Kuralları ve Sadeleştirme

4. Logaritmik Denklemler

5. Logaritma-Üstel Karışık Sorular ve Uygulamalar

6. Grafik ve Yorum Soruları

Logaritmanın Tanımı ve Üstel Fonksiyonlarla İlişkisi

📘 A. Logaritmanın Tanımı

​

Yani:
“b tabanında a’nın logaritması x’tir”, çünkü b üzeri x = a eder.

📌 Burada:

• a > 0

• b > 0  ve b ≠ 1 

📘 B. Logaritma ve Üstel Fonksiyonlar Arasındaki Bağlantı

📘 C. Özel Tanımlar

📘 D. 10 Tabanı ve e Tabanı

Logaritmanın Temel Özellikleri

📘 A. Tanım Koşulları

​

ifadesinin tanımlı olması için:

📌 a ya da b negatif olamaz, b 1 olamaz.

📘 B. Temel Özdeşlikler (Kural Gibi Kullanılır)

📘 C. Taban ve Değerin Yer Değişimi

Logaritmanın Kuralları ve Sadeleştirme

📘 A. Logaritmanın Temel Kuralları

Bu kurallar sayesinde logaritmik ifadeleri ayırabilir, birleştirebilir veya sadeleştirebiliriz.

🔹 1. Çarpım Kuralı

​

🔹 2. Bölme Kuralı

​

🔹 3. Üs Kuralı

📘 B. Sadeleştirme ve Yazım Teknikleri

Bazen ifadeler parçalanır:

Veya:

📘 C. Taban Değiştirme Formülü

En yaygın hali:

🎓 Örnek:

Logaritmik Denklemler

📘 A. Denklem Çözümünde Genel Strateji

Bir logaritmik denklem çözülürken:

1. Tanım kümesi mutlaka kontrol edilir

2. Gerekirse logaritma kuralları (çarpım, bölme, üs) uygulanır

3. Her iki taraf aynı tabanda ise, logaritmalar atılır

4. Üstel forma geçilebilir:

📘 B. Her İki Taraf Logaritmalıysa

Eğer:

📘 C. Tabanlar Aynı Değilse → Log kurallarıyla çözülür

🎓 Örnek 4:

📘 D. İki Log Toplamlıysa

🎓 Örnek 5:

Logaritma – Üstel Karışık Sorular ve Uygulamalar

📘 A. Logaritmalı Üstel Denklemler

Bu tarz sorularda:

• Üstel ifadeyi logaritmaya, logaritmayı üsse dönüştürerek

• Denklem sadeleştirilerek çözülür

📘 B. Fonksiyonlu Logaritma Soruları

📘 C. Uygulamalı – Problem Tarzı Sorular

Örnek 5:

Bir bakterinin sayısı her 1 saatte 2 katına çıkıyor.
Başlangıçta 1 adet varsa, t saat sonra bakteri sayısı kaçtır?

🎯 Sık Hatırlanan Bağlantılar:

Grafik ve Yorum Soruları – Son Madde Tekrarı

📘 C. Logaritma Grafiği Üzerinden Taban Yorumu

Verilen:
Bir  grafiği (1, 0) noktasından geçiyorsa bu ne anlama gelir?

🔹 Cevap:

Bu, logaritma fonksiyonunun tanımı gereğidir.

Dolayısıyla her logaritmik fonksiyon mutlaka (1, 0) noktasından geçer.

Yani:

Logaritma AYT Deneme Testi

(Cevap anahtarı en altta)