AYT Matematik Mantık Konu Anlatımı

Mantık, matematiksel düşünmenin temelidir.
AYT’de bu konu genellikle:

• Önermeler

• Doğruluk değerleri

• Birleşik önermeler

• Denk önermeler

• Doğruluk tabloları

• İkilem, çelişki, totoloji

• Niceleyicili ifadeler
  konularını içerir.

Bu bölümde işlemler genellikle sözlü ve sembolik ifade yorumlamaya dayanır.

🔹 Mantık Ünitesinin Alt Başlıkları:

1. Önermeler ve Doğruluk Değeri

2. Birleşik Önermeler (ve, veya, değil)

3. Koşullu ve İki Yönlü Önermeler

4. Doğruluk Tabloları ve Denk Önermeler

5. Totoloji – Çelişki – İkilem

6. Nicel Mantık (Her, Bazı, En Az Biri…)

🎯 AYT’de Bu Konu Nasıl Sorulur?

• “Verilen ifade aşağıdakilerden hangisiyle denktir?”

• “Bu önerme hangi durumda doğrudur?”

• “Önermenin olumsuzu nedir?”

• “İkilem – çelişki – totoloji tanıma dayalı soru”

• “Her, bazı gibi niceleyicili ifadelerin doğruluk analizi”

Önermeler ve Doğruluk Değeri

📘 Önerme Nedir?

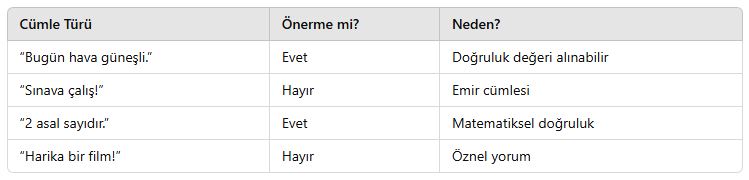
Önerme, doğru ya da yanlış olduğu kesin olarak bilinebilen anlamlı cümlelerdir.

Bir önerme:

• Kesinlikle doğru olabilir (Doğruluk değeri: 1)

• Kesinlikle yanlış olabilir (Doğruluk değeri: 0)

🧠 Örnek – Önerme Olan Cümleler:

• “2 asal bir sayıdır.” → ✅ (Doğru → 1)

• “5 + 4 = 11” → ✅ (Yanlış → 0)

• “Ankara Türkiye’nin başkentidir.” → ✅ (Doğru)

❌ Önerme Olmayan Cümleler:

• “Kapıyı kapat.” → Emir cümlesi

• “Acaba dışarıda yağmur yağıyor mu?” → Soru cümlesi

• “Keşke bugün tatil olsa.” → Dilek – temenni

• “Bu çok güzelmiş.” → Yorum – öznel yargı

Bu tür cümleler önerme değildir çünkü doğruluk değeri belirli ve kesin değildir.

🎯 Önermelerin Sembol Gösterimi:

Önermeler genellikle küçük harflerle (p, q, r…) gösterilir.

Örneğin:

Buradaki D(p), “p önermesinin doğruluk değeri” anlamına gelir.

📌 Dikkat Edilecek Noktalar:

Mini Alıştırmalar:

Aşağıdaki cümlelerin önerme olup olmadığını ve varsa doğruluk değerini belirtin:

1. “7 asal bir sayıdır.”

2. “Kapıyı aç.”

3. “Ay, Dünya’nın uydusudur.”

4. “5 + 3 = 10”

5. “Keşke tatil olsa.”

✅ Cevaplar:

1. ✅ Önerme – Doğru → D = 1

2. ❌ Önerme değil – emir cümlesi

3. ✅ Önerme – Doğru → D = 1

4. ✅ Önerme – Yanlış → D = 0

5. ❌ Önerme değil – dilek cümlesi

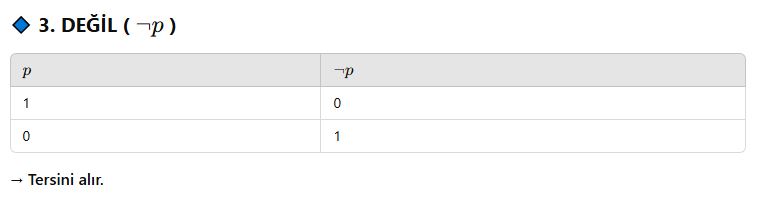
Birleşik Önermeler (ve, veya, değil)

📘 Tanım:

Birleşik önerme, birden fazla önermenin mantıksal bağlaçlarla birleştirilmesiyle oluşur.

Kullanılan bağlaçlar:

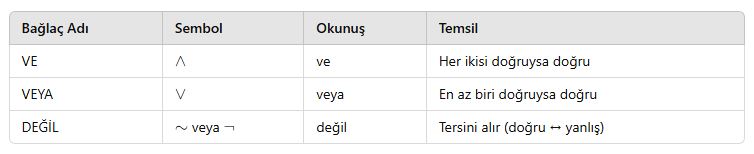
🎯 Doğruluk Tabloları

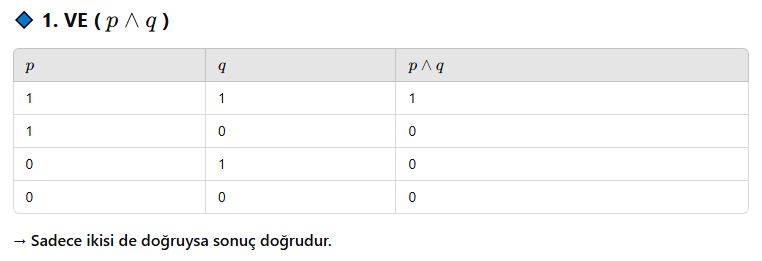
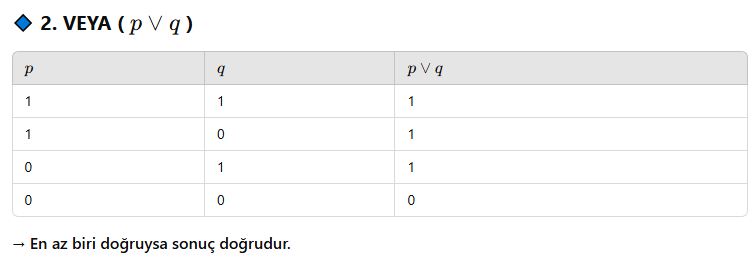
🔎 Sözlü ifadelerle mantık eşlemesi:

Koşullu ve İki Yönlü Önermeler

📘 A. Koşullu Önerme (İse – p⇒q)

Bu tür önermeler:

“Eğer p, ise q”
“p olursa, q da olur”

şeklinde okunur.
Sembol: p⇒q

🎯 Doğruluk Tablosu:

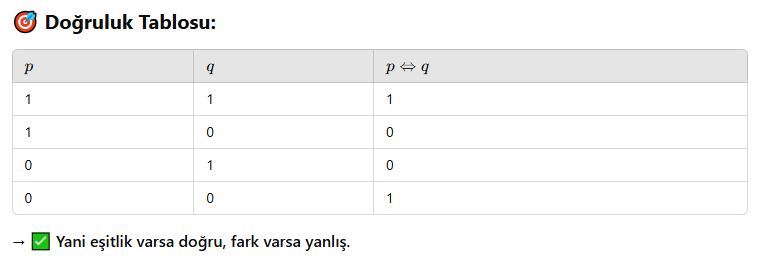
📘 B. İki Yönlü Önerme (Ancak ve Ancak – p⇔q)

Bu tür önermeler:

“p ancak ve ancak q ise doğrudur”
“p ile q aynı doğruluk değerine sahipse doğru olur”

Sembol: p⇔q

🎓 Örnek:

p: “Sayı çifttir.”
q: “Sayı 2 ile tam bölünür.”

• p⇒q: Eğer sayı çifttir, o halde 2 ile bölünür. ✅

• Tersi: “Sayı tekse, 2 ile bölünemez.”

• Karşıtı: “2 ile bölünmüyorsa, sayı tek sayı olabilir.”

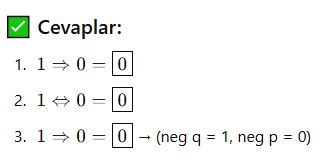
Doğruluk Tabloları ve Denk Önermeler

📘 A. Doğruluk Tablosu Nedir?

Bir veya birden fazla önermenin, her olası doğruluk durumundaki mantıksal değerlerini tablo hâlinde göstermeye doğruluk tablosu denir.

Önermeler p, q gibi değişkenlerden oluşur. Her biri için:

• 1 → Doğru

• 0 → Yanlış

olarak değerlendirme yapılır.

🧠 İki Önermede Kaç Satır Olur?

Her önerme için 2 durum (1 ve 0) olduğundan:

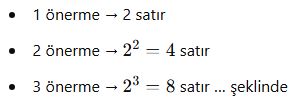
🎯 B. Denk Önermeler

İki önerme her olası durumda aynı doğruluk değerine sahipse, bu iki önerme denk önermelerdir.
Sembol:

p ≡ q

Aynı doğruluk sütununa sahipse → denktir
Farklı bir yerde bile fark varsa → denk değildir

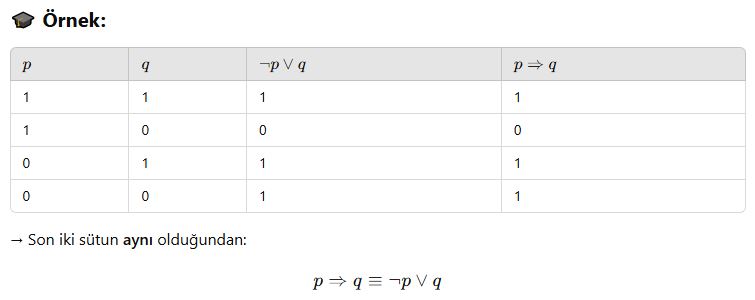
Bu AYT’de çok sık sorulan bir denk önerme eşitliğidir.

✅ Bazı Önemli Denk Önermeler:

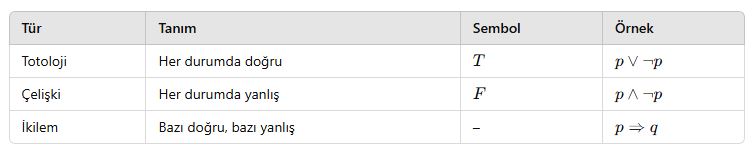
Totoloji – Çelişki – İkilem

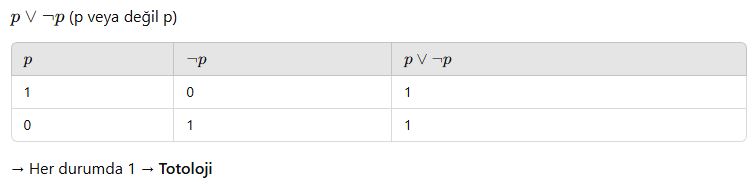
📘 A. Totoloji Nedir?

Bir birleşik önerme, tüm olası durumlarda doğruysa, buna totoloji denir.

Her doğruluk satırında sonuç 1 → Totolojidir
Sembol: genellikle $T$ ile gösterilir

📘 B. Çelişki Nedir?

Bir birleşik önerme, her durumda yanlışsa, buna çelişki denir.

Tüm satırlarda sonuç 0 → Çelişkidir
Sembol: genellikle $F$

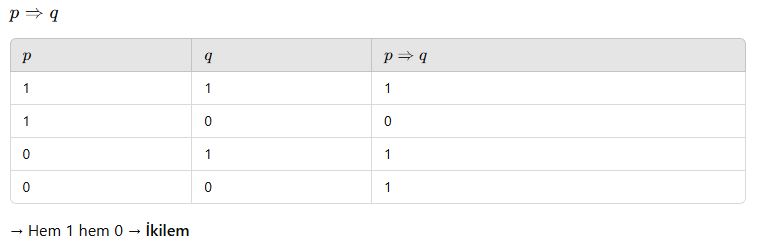
📘 C. İkilem Nedir?

Birleşik önerme, bazı durumlarda doğru, bazı durumlarda yanlışsa → ikilem denir.

🎓 Örnekler:

✅ Totoloji Örneği:

❌ Çelişki Örneği:

⚖️ İkilem Örneği:

🧠 Özet Tablo:

Nicel Mantık (Her, Bazı, En Az Biri…)

📘 Nicel Mantık Nedir?

Nicel mantık, özneye ilişkin “kaç kişi / kaç nesne” ile ilgili bilgileri içeren önermelerin yorumlanmasıdır.

Bu ifadeler:

Bu semboller özellikle üniversite sınavı mantık sorularında çok karşımıza çıkar.

🧠 Temel Yorumlar:

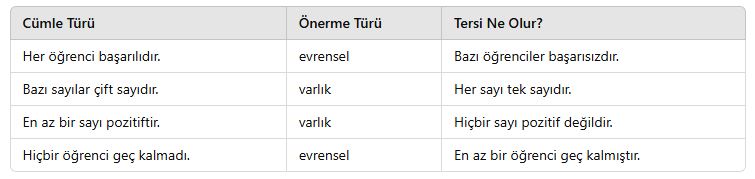
🎯 Olumsuzlarını Alırken:

• “Her” ifadesinin olumsuzu → “Bazı … değil”

• “Bazı” ifadesinin olumsuzu → “Her … değil”

Örnek:

• Her doğal sayı pozitiftir.
  ❌ Olumsuz: “Bazı doğal sayılar pozitif değildir.” (0 örneğiyle desteklenir)

🎓 Örnek 1:

“Her asal sayı 2’den büyüktür.”
→ Doğru mu?

❌ Hayır. Çünkü 2 asal sayıdır ama 2’den büyük değildir.
→ Tersi: “Bazı asal sayılar 2’den büyük değildir.” ✅

🎓 Örnek 2:

“Bazı üçgenlerin iç açılar toplamı 180°’dir.”
→ ❌ Yanlış! Çünkü bu ifade tüm üçgenler için geçerli.

Doğrusu: “Her üçgenin iç açılar toplamı 180°’dir.”

🧠 Sınavda dikkat:

• “Her” → genelleme → 1 örnekle çürütülebilir

• “Bazı” → varlık → en az bir tane varsa doğrular

🔧 Mini Alıştırmalar:

1. “Her asal sayı tektir.” → Doğru mu? Tersi?

2. “Bazı doğal sayılar çifttir.” → Doğru mu?

3. “Hiçbir öğrenci başarısız değildir.” → Ne anlama gelir?

4. “Bazı sayılar negatif değildir.” → Denk ifade?

✅ Cevaplar:

1. ❌ Yanlış (çünkü 2 çifttir) → Tersi: “Bazı asal sayılar tek değildir.”

2. ✅ Doğru (örneğin 2, 4…)

3. “Tüm öğrenciler başarılıdır.”

4. “En az bir sayı pozitiftir.”

Ayt Mantık – 10 Soruluk Değerlendirme Testi

Her soru farklı bir alt başlıktan seçildi.
Cevap anahtarı en altta.

1. (Önerme Tanımı)

Aşağıdakilerden hangisi bir önermedir?

A) Lütfen kapıyı kapat.
B) 7 asal bir sayıdır.
C) Keşke hava güzel olsa.
D) Çok sıcak burası.

2. (Doğruluk Değeri)

p: 9 asal bir sayıdır.
Bu önermenin doğruluk değeri nedir?

A) 0
B) 1
C) Hem 0 hem 1
D) Belirsiz

5. (Koşullu Önerme)

Aşağıdaki önermelerden hangisi koşullu (→) yapıya örnektir?

A) Bugün hava yağmurlu değil.
B) Bazı insanlar kitap okumayı sever.
C) Eğer sınava çalışırsan, başarılı olursun.
D) Ay, Dünya’nın uydusudur.

10. (Nicel Mantık)

“Her asal sayı çifttir.” önermesinin tersi nedir?

A) Her asal sayı tek değildir.
B) Bazı asal sayılar tek değildir.
C) Bazı asal sayılar çift değildir.
D) Bazı asal sayılar çift değildir.