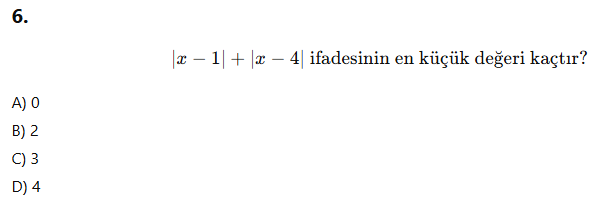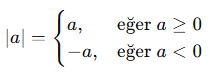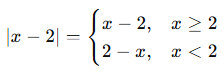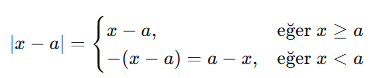AYT Matematik Mutlak Değer Konu Anlatımı ve Örnek Sorular

AYT Matematik Mutlak Değer Konu Anlatımı

📘 Mutlak Değer Nedir?

Bir gerçek sayının, sayı doğrusundaki 0 noktasına olan uzaklığına mutlak değer denir.

Mutlak değer sonucu her zaman pozitif ya da sıfırdır.

Matematiksel gösterimi:

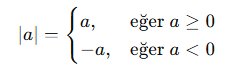
🔍 Temel Özellikler:

🧠 Bazı Bilinmesi Gereken Değerler:

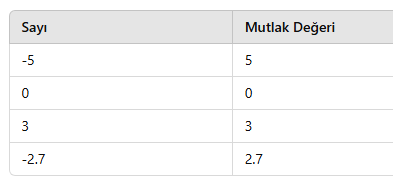
🎓 Örnek 1:

🎓 Örnek 2:

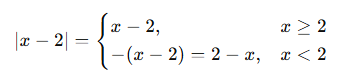
🎯 Mutlak Değer Ne Zaman Sorulur?

• Eşitsizlikler içinde

• Denklemlerde

• Parçalı fonksiyonlar içinde

• Grafik yorumlarında

• Gerçek hayat senaryolarında (mesafe, tolerans vb.)

📌 Ünitedeki Alt Başlıklar:

1. Mutlak Değer Tanımı ve Özellikleri

2. Mutlak Değerli İfadelerin Açılımı (Parçalı Hâli)

3. Mutlak Değerli Denklem Çözümü

4. Mutlak Değerli Eşitsizlikler

5. Birden Fazla Mutlak Değerli İfade ile Problem Çözümü

6. Geometrik ve Grafiksel Yorumlar (AYT Seviyesi)

Mutlak Değer Tanımı ve Özellikleri

📘 Tanım:

Bir gerçek sayının 0’a olan uzaklığına mutlak değer denir ve |a| şeklinde gösterilir.

Yani:

​

✔ Uzaklık kavramı olduğu için negatif olmaz
✔ 0’ın mutlak değeri yine 0’dır
✔ İşareti ortadan kaldıran bir işlemdir

Örneklerle Tanımı Pekiştirelim:

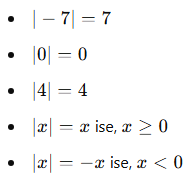
🔹 Mutlak Değerin Temel Özellikleri

Mutlak değer işlemi sırasında aşağıdaki kurallar çok önemlidir 👇

🔸 1. |a| ≥ 0

Her sayının mutlak değeri sıfıra eşit ya da sıfırdan büyüktür.

🔸 2. |a| = |-a|

Bir sayının ve tersinin mutlak değeri aynıdır.
Örnek:

🔸 3. |a·b| = |a| · |b|

Çarpma işlemi mutlak değer içine dağılır.
Örnek:

Kesirli ifadede hem payın hem paydanın mutlak değeri alınabilir.
Örnek:

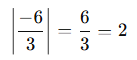
Mutlak değer karesi, sayının karesine eşittir.
Örnek:

İki sayı arasındaki uzaklık daima pozitiftir ve değişme özelliği vardır.

Örnek:

🎓 Karma Örnekler:

🔹 Örnek 1:

🔹 Örnek 2:

​

(Dikkat: Sonuç negatif olabilir çünkü arada işlem var, mutlak değer değil.)

🔹 Örnek 3:

​

🧠 Dikkat Edilmesi Gerekenler (AYT İpuçları):

• Mutlak değer dışındaki işlemlerde sonucun negatif olması mümkündür.

• Parçalı tanımı özellikle eşitsizlik ve denklem çözümünde kritik rol oynar.

• Mutlak değer uzaklık olduğundan geometrik yorumlarda da karşımıza çıkar.

• Mutlak değer kareye alınırsa açılmadan işlem yapılabilir.

Mutlak Değerli İfadelerin Açılımı (Parçalı Hâli)

📘 Tanım:

Bir mutlak değerli ifade, içindeki ifadenin işaretine göre farklı değerler alabilir. Bu yüzden mutlak değerli ifadeler, parçalı fonksiyon gibi yazılabilir.

🔹 Temel Kalıp:

​

Bu açılım; grafik çizimi, eşitsizlik çözümü ve yorumlarda kritik öneme sahiptir.

🎓 Örnekler Üzerinden Gidelim:

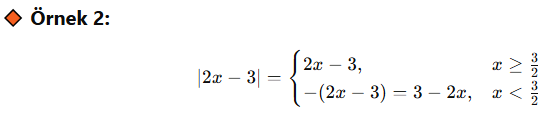
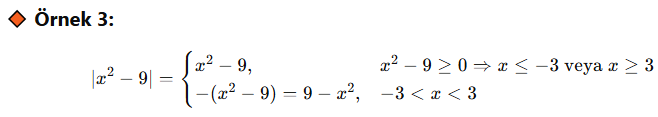
📌 Gördüğün gibi, mutlak değerin içindeki ifadeye göre eşitsizlik kurarak hangi parçada ne yazılacağını belirliyoruz.

📏 Genel Açılım Şablonu:

Eğer

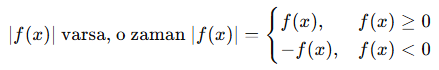
Yani f(x)’in sıfır olduğu değerler kritik noktadır. Bu noktalara göre sağında ve solunda mutlak değerli ifade farklı şekilde açılır.

🧠 AYT İpuçları:

• Mutlak değerli ifadeyi parçalayabilmek için önce sıfır yapan noktayı bulmalısın.

• Açılımı doğru yapmazsan denklem/eşitsizlik hatalı çıkar

• Mutlak değerli fonksiyonların grafikleri de parçalı olarak çizilir

• AYT’de genellikle birden fazla mutlak değer içeren sorular parçalara ayrılarak çözülür

Mutlak Değerli Denklem Çözümü

📘 Temel Kural:

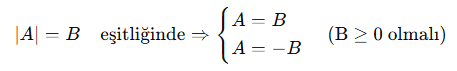
Yani mutlak değerli bir denklem, iki farklı denklem şeklinde çözülür.
Fakat burada önemli bir şart var:

B negatifse denklem çözüm kümesi boş olur. Çünkü mutlak değer hiçbir zaman negatif olamaz!

🎓 Örnek 1:

📌 Çözüm:

✔ Çözüm kümesi:

🎓 Örnek 2:

❌ Mutlak değer negatif olamaz
✔ Çözüm kümesi: ∅​ (boş küme)

🎓 Örnek 3:

📌 Bu tarzda iki taraflı mutlak değer varsa 3 durum incelenir:

🔸 Durum 1:

🔸 Durum 2:

✔ Çözüm kümesi:

Mutlak Değerli Eşitsizlikler

📘 Temel Yapı:

Mutlak değerli eşitsizlikler, genellikle şu iki formdadır:

Yani bir aralık elde ederiz.

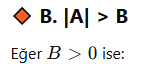
Yani birleşik (iki parça) çözüm çıkar.

❗ Önemli Not:

Eğer B < 0 ise, mutlak değerli ifade asla negatif olamayacağı için:

🎓 Örnekler Üzerinden Gidelim

🔹 Örnek 1:

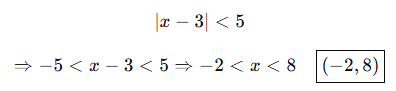
🔹 Örnek 2:

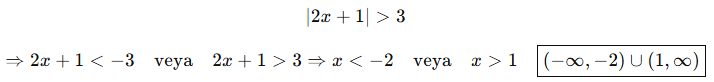
🔹 Örnek 3:

🔹 Örnek 4 – Denklemle birleşik:

📏 Genel Çözüm Özet Tablosu:

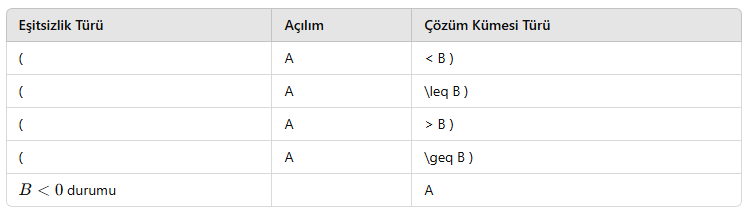
AYT Düzeyinde İpuçları:

• Karmaşık eşitsizliklerde mutlaka içi açmadan önce işaret kontrolü yap

• Köklü ifadelerle birlikte verildiyse tanım aralığına dikkat et

• Sonuçta sayı doğrusu, aralık ya da küme ile ifade istenebilir

• Eşitlik içeriyorsa kapalı aralık; içermiyorsa açık aralık kullanılır

Birden Fazla Mutlak Değerli İfade ile Problem Çözümü

Birden fazla mutlak değer içeren ifadelerle karşılaştığımızda, doğrudan işlem yapmak yerine, her bir ifadenin sıfır olduğu noktaları (kritik değerler) tespit ederiz. Bu kritik noktalarla sayı doğrusunu parçalara ayırır, her aralıkta mutlak değerleri işaretlerine göre açar, sonra çözüm yaparız.

📘 Konu Özeti:

Birden fazla mutlak değerli ifade varsa:

• Her birinin sıfır yapan değeri (kritik nokta) bulunur

• Sayı doğrusu bu noktalara göre bölümlere ayrılır

• Her aralıkta mutlak değerler işaretlerine göre açılır

• Her aralık ayrı ayrı çözülür, sonra uygun çözümler birleştirilir

Adım Adım Strateji:

1. Her mutlak değerin sıfır olduğu noktayı bul

2. Sayı doğrusunda kritik noktaları sırala

3. Oluşan aralıkları belirle

4. Her aralıkta mutlak değerleri işarete göre aç

5. Denklem ya da eşitsizliği çöz

6. Koşula uyan çözümleri topla

🎓 Örnek 1 – Denklem Tipi:

📌 Kritik noktalar:

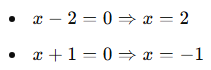
Bu noktalar sayı doğrusunu 3 parçaya ayırır:

🔹 1. Aralık:

Her iki mutlak değer negatif çıkar:

✅ Bu çözüm, x < -1 koşulunu sağlar.

🔹 2. Aralık: 

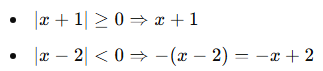
✅ Bu da x ≥ 2 koşulunu sağlar.

🎓 Örnek 2 – Eşitsizlik Tipi:

📌 Kritik noktalar: x = -2 ve x = 4
Sayı doğrusunda 3 parça oluşur:

🔹 1. Aralık: 

Her iki mutlak değer negatif çıkar:

Bu koşul, x<−2 ile kesişirse:

🔹 2. Aralık:

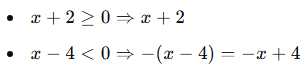
Toplam:

🔹 3. Aralık:

Her ikisi pozitif çıkar:

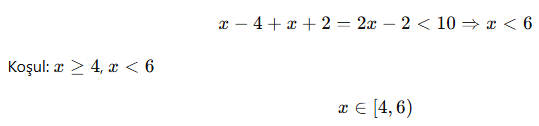
🧠 AYT’de Dikkat Edilecekler:

• Mutlak değer sayısı arttıkça aralık sayısı da artar

• Her aralığın koşulu mutlaka kontrol edilmelidir

• Parçalı çözüm mantığı, grafik ve fonksiyon yorumlarıyla da birleşebilir

• Eşitsizliklerde cevap birleşim kümesi şeklinde olabilir

Mutlak Değerin Grafiksel ve Geometrik Yorumu

📘 A. Grafiksel Yorum – Fonksiyon Olarak Mutlak Değer

En temel mutlak değer fonksiyonu:

Bu fonksiyonun grafiği:

• x = 0 noktasında tepe yapar (V şeklindedir)

• Sağ kolda y = x doğrusu gibi davranır

• Sol kolda y = -x doğrusu gibi davranır

🔹 f(x) = |x| Grafiği Özellikleri

• Tepe noktası: (0, 0)

• Simetrik: y eksenine göre simetriktir

• Tanım kümesi: ℝ

• Değer kümesi: [0,∞)

🎓 Örnek 1 – f(x) = |x – 3|

Bu fonksiyon, f(x) = |x|‘in x ekseni boyunca 3 birim sağa ötelenmiş halidir.

• Tepe noktası: (3, 0)

• Sağda y = x – 3, solda y = -(x – 3)

🎓 Örnek 2 – f(x) = |x + 2| + 1

• ∣x+2∣: sola 2 birim öteleme

• +1: yukarı 1 birim dikey kayma

• Tepe noktası: (-2, 1)

🧠 AYT Sorularında Neler Sorulabilir?

• Grafiğin tanım/değer kümesi

• Minimum değeri

• Bir aralıkta fonksiyonun sabit/azalan/artan olup olmadığı

• f(x) = a, f(x) < b gibi grafikten çözüm kümesi bulma

📘 B. Geometrik Yorum – Sayı Doğrusu ve Uzaklık

Mutlak değerin geometrik anlamı, iki sayı arasındaki uzaklıktır:

Özellikle eşitsizliklerde şu çok sık kullanılır:

🎓 Örnek 4:

|x – 4| + |x – 1| ifadesinin en küçük değeri nedir?

Bu tür soruların genel mantığı şudur:

İki noktaya olan toplam mesafenin en az olduğu nokta, bu iki noktanın arasındadır.

Burada sayı doğrusu üzerindeki iki nokta: 1 ve 4
En küçük toplam uzaklık, bu iki nokta arasında bir yerde olur.
En küçük değer:

Minimum değer: farkın kendisi = 3

🧠 AYT’de Dikkat Edilecek Noktalar:

• Grafik okuma becerisi çok önemlidir.

• Sayı doğrusu yorumları (en kısa, en uzun mesafe) sorulabilir

• Parçalı fonksiyonlarla mutlak değerin birleşimi gelir

• En küçük/en büyük değer yorumları mesafe üzerinden çıkarılır

• Grafik soruları genellikle şekille verilmiş olur, çözüm yorum gerektirir

AYT Matematik Mutlak Değer Testi