AYT Matematik Temel Kavramlar Konu Anlatımı

AYT Matematik, TYT’ye kıyasla daha derin kavrayış gerektiren, zorlayıcı ve analitik düşünmeyi ön plana çıkaran bir sınavdır. Bu nedenle konular yalnızca yüzeysel bilgilerle değil, mantıksal ilişkilerle ele alınmalı, zorlayıcı örneklerle desteklenmelidir. Matematikte başarılı olmanın temeli, sayıların ve onların özelliklerinin iyi anlaşılmasına dayanır. “Temel Kavramlar” ünitesi, AYT’de karşılaşılacak ileri seviye problemlerin temelini oluşturur ve bu üniteye hâkim olan bir öğrenci, ilerleyen konularda çok daha rahat ilerleyebilir.

Bu ünitede sayılar ve sayı kümeleri üzerinde durarak, sayıların farklı türlerini, aralarındaki ilişkileri ve özelliklerini detaylıca ele alacağız. Sayıların yapısını anlamak, işlem becerilerini geliştirmek ve sayı kümelerinin nasıl kullanıldığını kavramak, matematikte sağlam bir temel oluşturacaktır. Örneğin, asal sayılar, ardışık sayılar ve faktöriyel gibi kavramlar, ilerleyen kombinatorik, fonksiyonlar ve türev gibi konularda karşımıza çıkacaktır. Ayrıca, sayı kümeleri arasındaki ilişkileri iyi anlamak, karmaşık problemlerde doğru stratejiyi belirleyebilmek adına kritik öneme sahiptir.

Rakam ve Sayı

Matematikte en temel kavramlardan biri rakam ve sayı arasındaki farktır. Pek çok öğrenci bu iki kavramı karıştırabilir. Oysa ki, bu iki kavram birbirinden farklıdır ve sayıların anlaşılmasında temel bir rol oynar.

• Rakam: Sayıları oluşturmak için kullanılan sembollerdir. 0, 1, 2, 3, 4, 5, 6, 7, 8 ve 9 olmak üzere toplam 10 tane rakam vardır.
• Sayı: Bir veya birden fazla rakamın bir araya gelmesiyle oluşan matematiksel ifadelerdir. Örneğin, 27 bir sayıdır ve 2 ile 7 rakamlarından oluşur.

Örneğin:

• 5 bir rakamdır ama aynı zamanda bir sayıdır.
• 357 bir sayıdır ve içinde 3, 5 ve 7 rakamları bulunur.

Matematikte sayıların sınıflandırılması oldukça geniştir. AYT’de rakamlar genellikle basamak kavramıyla birlikte ele alınır ve sayı sistemlerinde sıkça kullanılır.

Doğal Sayılar

Doğal sayılar, en temel sayı kümelerinden biridir ve günlük hayatta sıkça kullanılır. Matematikte N harfi ile gösterilir:

N={0,1,2,3,4,5,6,7,…}

Özellikleri:

1. En küçük doğal sayı 0’dır.
2. Doğal sayılar kümesi negatif sayıları içermez.
3. Sonsuz elemanlı bir kümedir, çünkü doğal sayılar her zaman bir fazlası alınarak büyütülebilir.

Örnek Sorular:

1. Aşağıdaki ifadelerden hangisi doğal sayılar kümesine aittir?
   A) -5 B) 0 C) 2.3 D) √2

   Çözüm: Doğal sayılar negatif sayıları ve ondalıklı sayıları içermez. Doğru cevap B) 0 olacaktır.

2. İki ardışık doğal sayının toplamı 17 olduğuna göre, bu sayılar kaçtır?

   Çözüm: Ardışık iki doğal sayıyı x ve x+1 olarak alırsak:

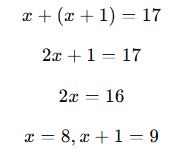
Doğru cevap: 8 ve 9’dur.

Sayma Sayıları

Sayma sayıları, günlük hayatta nesneleri saymak için kullandığımız sayılardır ve 1’den başlayarak sonsuza kadar gider. Matematikte N⁺ (N pozitif) harfi ile gösterilir:

Özellikleri:

1. 0 sayma sayılarına dahil değildir.
2. Negatif sayılar sayma sayıları kümesine ait değildir.
3. Herhangi iki ardışık sayma sayısının farkı 1’dir.

Örnek Soru:
Bir çocuğun 10’dan küçük oyuncak arabaları vardır. Eğer bir araba daha alırsa toplam kaç tane arabası olur?

Çözüm: Sayma sayıları ardışık olarak ilerlediğinden, 10’dan küçük olan en büyük sayma sayısı 9’dur. Bir araba daha eklersek:

9+1=10

Cevap: 10 araba olur.

Tam Sayılar Kümesi

Tam sayılar kümesi, negatif ve pozitif tam sayılar ile sıfırdan oluşan geniş bir sayı kümesidir. ℤ harfi ile gösterilir.

Özellikleri:

1. Doğal sayıları da içerir, ancak negatif sayılar da tam sayılar kümesine dâhildir.
2. Sıfır (0) tam sayı kümesine aittir, ancak pozitif veya negatif değildir.
3. İki tam sayının toplamı ve çarpımı yine tam sayıdır.
4. İki tam sayının farkı her zaman tam sayı olmak zorunda değildir. Örneğin:
   • 2 – 5 = -3 (Tam sayı) ✅
   • 2 ÷ 5 = 0.4 (Tam sayı değil) ❌

Örnek Soru:

Bir tam sayının karesi her zaman pozitiftir. Bu ifade doğru mu?

Cevap: Evet, bir tam sayının karesi her zaman sıfırdan büyük ya da sıfırdır.
Örneğin:

• (-3)² = 9
• (5)² = 25
• (0)² = 0

Doğru cevap: “Evet” ✅

Rasyonel Sayılar (ℚ)

Rasyonel sayılar, bir tam sayının başka bir tam sayıya bölümüyle ifade edilebilen sayılardır. Yani a/b şeklinde yazılabilen tüm sayılar rasyoneldir (b ≠ 0 olmak şartıyla).

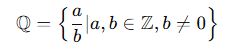
Örneğin:

• 1/2, -5/3, 0.75, 4 (çünkü 4 = 4/1)

Özellikleri:

1. Sonlu veya periyodik ondalık kesir olarak yazılabilirler.
   • Örneğin, 0.75 = 75/100
2. Her tam sayı bir rasyonel sayıdır. Örneğin 5 = 5/1
3. İki rasyonel sayının toplamı, farkı ve çarpımı yine rasyonel sayıdır.
4. İki rasyonel sayının bölümü rasyonel olmayabilir. Örneğin:
   • 4 ÷ 0 tanımsızdır ❌

Örnek Soru:

Aşağıdaki sayılardan hangisi rasyonel değildir?
A) 7
B) -3/4
C) √2
D) 0.3333… (devam eden periyodik sayı)

Çözüm:

• 7, bir tam sayı olduğu için rasyoneldir. ✅
• -3/4, iki tam sayının bölümü olduğundan rasyoneldir. ✅
• √2, bir tam sayının bölümü olarak yazılamaz, bu yüzden irrasyoneldir. ❌
• 0.3333…, 1/3 şeklinde yazılabildiğinden rasyoneldir. ✅

Cevap: C) √2 ✅

İrrasyonel Sayılar (ℝ – ℚ)

İrrasyonel sayılar, kesir olarak yazılamayan, ondalık gösterimi sonsuz ve düzensiz olan sayılardır.

Örneğin:

• √2 = 1.414213…
• π (Pi) = 3.141592653…
• e (Euler sayısı) = 2.71828…

Özellikleri:

1. Kesir olarak gösterilemezler.
2. Ondalık gösterimleri sonsuz ve düzensizdir. (Örneğin, π sonsuza kadar devam eder.)
3. İki irrasyonel sayının toplamı bazen rasyonel olabilir. Örneğin:
   • (√2 – √2) = 0 (Rasyonel oldu!) ✅
4. İki irrasyonel sayının çarpımı rasyonel olabilir.
   • √2 × √2 = 2 (Bu bir tam sayı!) ✅

Örnek Soru:

Aşağıdaki sayılardan hangisi irrasyoneldir?
A) -5/2
B) π
C) 2.5
D) 16/3

Çözüm:

• -5/2, iki tam sayının bölümü olduğu için rasyoneldir. ✅
• π, ondalık olarak düzensiz devam eden bir sayı olduğu için irrasyoneldir. ❌
• 2.5, 5/2 şeklinde yazılabileceği için rasyoneldir. ✅
• 16/3, bir tam sayının bölümü olduğu için rasyoneldir. ✅

Cevap: B) π ✅

Çift Sayılar ve Tek Sayılar

Çift sayılar, 2 ile tam bölünebilen tam sayılardır.

Tek sayılar, 2 ile tam bölünemeyen tam sayılardır.

Matematikte çift ve tek sayılar ile ilgili bazı temel kurallar:

1. İki çift sayının toplamı çifttir.
   • Örnek: 4 + 6 = 10 (Çift)
2. İki tek sayının toplamı çifttir.
   • Örnek: 5 + 3 = 8 (Çift)
3. Bir çift sayı ile bir tek sayının toplamı tektir.
   • Örnek: 4 + 7 = 11 (Tek)
4. İki çift sayının çarpımı çifttir.
   • Örnek: 6 × 8 = 48 (Çift)
5. İki tek sayının çarpımı tektir.
   • Örnek: 3 × 5 = 15 (Tek)

Örnek Soru:

x ve y tek sayı olmak üzere, aşağıdaki işlemlerden hangisinin sonucu çifttir?
A) x + y
B) x × y
C) x²
D) x × y + 1

Çözüm:

• x + y, iki tek sayının toplamı olduğundan çifttir. ✅
• x × y, iki tek sayının çarpımı tektir. ❌
• x², tek sayının karesi yine tektir. ❌
• x × y + 1, tek bir sayıya 1 eklediğimiz için çift olur. ❌

Cevap: A) x + y ✅

Pozitif Sayılar ve Negatif Sayılar

Pozitif ve negatif sayılar, sayı doğrusu üzerinde sıfırın sağında ve solunda yer alan iki temel sayı grubudur. Matematikte birçok işlem ve problem çözümünde pozitif ve negatif sayılarla karşılaşırız.

Pozitif Sayılar:

Pozitif sayılar, sıfırdan büyük olan sayılardır ve “+” işareti ile gösterilir. Ancak genellikle işaret belirtilmeden yazılır.

Örneğin:

Özellikleri:

1. Pozitif sayılar sıfırdan büyüktür.
2. Pozitif sayılar kendi arasında toplandığında sonuç her zaman pozitiftir.
3. Pozitif sayılar çarpıldığında sonuç her zaman pozitiftir.

Negatif Sayılar:

Negatif sayılar, sıfırdan küçük olan sayılardır ve “-” işareti ile gösterilir.

Örneğin:

Özellikleri:

1. Negatif sayılar sıfırdan küçüktür.
2. Negatif sayılar toplandığında, daha küçük olan sayının mutlak değeri büyükse sonuç negatif olur.
3. Negatif sayılar çarpıldığında çift sayıda negatif çarpan varsa sonuç pozitif, tek sayıda negatif çarpan varsa sonuç negatiftir.

Örnek Sorular ve Çözümleri:

Soru 1:
Aşağıdaki sayıların hangisi pozitiftir?
A) -8
B) 0
C) 5
D) -3

Çözüm: Pozitif sayılar sıfırdan büyük olan sayılardır. Doğru cevap C) 5 ✅

Soru 2:
(-7) + (+3) işleminin sonucu kaçtır?

Çözüm:

$$-7+3=-4$$

Çünkü negatif bir sayı ile pozitif bir sayı toplandığında mutlak değeri büyük olanın işareti alınır. Burada 7 > 3 olduğu için işaret negatif olur.

Cevap: -4 ✅

Soru 3:
(-4) × (-6) işleminin sonucu kaçtır?

Çözüm:
İki negatif sayının çarpımı pozitif olur.

$$(-4)\times (-6)=+24$$

Cevap: +24 ✅

Soru 4:
Aşağıdaki işlemlerden hangisinin sonucu negatiftir?
A) (-5) × (-2) × (-3)
B) (-4) × (-1) × (-2) × (-2)
C) (-6) × (-1)
D) (-7) × (-2) × (-1) × (-3) × (-2)

Çözüm:

• A şıkkında: Üç negatif sayı çarpıldığı için sonuç negatif olur. ✅
• B şıkkında: Dört negatif sayı çarpıldığı için sonuç pozitif olur. ❌
• C şıkkında: İki negatif sayı çarpıldığı için sonuç pozitif olur. ❌
• D şıkkında: Beş negatif sayı çarpıldığı için sonuç negatif olur. ✅

Doğru cevap: A ve D şıklarıdır. ✅

Ardışık Sayılar

Ardışık sayılar, belirli bir kurala göre sıralanan ve sabit bir farkla artan ya da azalan sayılardır.

1. Ardışık doğal sayılar: 1,2,3,4,5,6,…
2. Ardışık tek sayılar: 1,3,5,7,9,…
3. Ardışık çift sayılar: 2,4,6,8,10,…
4. Ardışık tam sayılar: −3,−2,−1,0,1,2,3,…

Özellikler:

• İki ardışık doğal sayının farkı her zaman 1’dir.
• İki ardışık çift veya tek sayının farkı her zaman 2’dir.
• n adet ardışık sayının toplamı şu formülle bulunur:

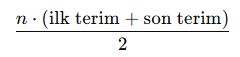
Örnek Soru:

Üç ardışık tek sayının toplamı 27 ise, en küçük sayı kaçtır?

Çözüm:
Ardışık tek sayıları x, x+2, x+4 şeklinde alabiliriz.

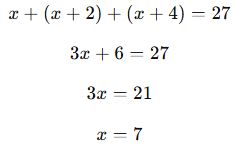
Cevap: 7 ✅

Asal Sayılar

Asal sayılar, yalnızca 1 ve kendisine tam bölünebilen 1’den büyük doğal sayılardır.

Örnek asal sayılar:

2,3,5,7,11,13,17,19,23,29,…

Özellikleri:

1. En küçük asal sayı 2’dir ve tek çift asal sayıdır.
2. Her asal sayı tek olmak zorunda değildir, örneğin 2 asal sayıdır.
3. Bir asal sayı yalnızca 1 ve kendisine bölünebilir.
4. 1 asal sayı değildir.
5. Asal sayılar birbirleriyle çarpılarak bileşik sayılar oluşturur.

Örnek Soru:
Aşağıdaki sayılardan hangisi asal sayıdır?
A) 15
B) 17
C) 21
D) 25

Çözüm:

• 15, 3 ve 5’e bölünebilir. Asal değildir. ❌
• 17, yalnızca 1 ve 17’ye bölünebilir. Asal sayıdır. ✅
• 21, 3 ve 7’ye bölünebilir. Asal değildir. ❌
• 25, 5’e bölünebilir. Asal değildir. ❌

Cevap: B) 17 ✅

Faktöriyel

Faktöriyel, bir sayının kendisinden küçük ve pozitif tam sayıların çarpımı olarak tanımlanır. Matematikte faktöriyel, “! (ünlem)” sembolü ile gösterilir.

Örneğin:

Faktöriyel, özellikle kombinasyon, permütasyon ve olasılık hesaplamalarında sıkça kullanılır.

Özellikleri:

1. 0! = 1 olarak kabul edilir.
   • Bunun sebebi matematiksel olarak tanımlanmıştır ve kombinatorik işlemlerde tutarlılığı sağlamak içindir.
2. 1! = 1’dir.
3. Bir faktöriyel sayısı, kendisinden bir önceki faktöriyel ile çarpılarak bulunabilir:
   

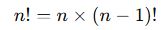
   Örneğin :
   

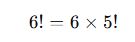
4. Büyük sayılarda faktöriyel hızla büyür:
   • 5! = 120
   • 6! = 720
   • 7! = 5.040
   • 8! = 40.320
   • 10! = 3.628.800
5. Faktöriyel işlemi sadece pozitif tam sayılar için tanımlıdır.

Örnek Soru:

Aşağıdaki işlemin sonucu kaçtır?

Cevap: 42 ✅

Örnek Soru:

Bir ürünün farklı 4 rengi vardır. Bu 4 rengi sıralı olarak dizmek için kaç farklı yöntem vardır?

Çözüm:
Bu sıralama işlemi faktöriyel ile hesaplanır:

Cevap: 24 farklı sıralama yöntemi vardır. ✅

Örnek Soru:

n!=120 eşitliğini sağlayan n değeri kaçtır?

Çözüm:
Faktöriyel değerlerini hesaplayarak:

• 3! = 6
• 4! = 24
• 5! = 120

Bu durumda, n = 5 olacaktır. ✅

Faktöriyel, özellikle kombinasyon, permütasyon, olasılık ve diziler gibi birçok matematiksel alanda sıkça karşımıza çıkar. Faktöriyel işlemlerinin hızlı büyümesi nedeniyle, büyük sayılar için hesaplama yaparken çarpanları sadeleştirmek oldukça faydalıdır.

AYT Matematik – Temel Kavramlar Deneme Soruları

1. Aşağıdaki ifadelerden hangisi doğrudur?

A) Her sayı bir rakamdır.
B) Rakamlar yalnızca 0 ile 9 arasındaki sayılardır.
C) Sayılar sadece pozitif olabilir.
D) Her rasyonel sayı aynı zamanda tam sayıdır.

2. Aşağıdaki ifadelerden hangisi irrasyonel bir sayıdır?

3. Aşağıdaki sayılardan hangisi asal sayı değildir?

A) 11
B) 23
C) 39
D) 47

4. 6!−4 işleminin sonucu kaçtır?

A) 672
B) 696
C) 710
D) 720

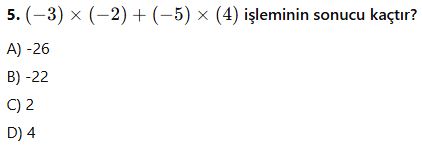
6. Aşağıdaki ifadelerden hangisi doğrudur?

A) İki negatif sayının toplamı daima negatiftir.
B) Bir negatif sayı ile bir pozitif sayının çarpımı pozitiftir.
C) Tüm çift sayılar asal sayıdır.
D) Rasyonel sayılar yalnızca tam sayılardan oluşur.

7. Aşağıdaki ifadelerden hangisi yanlıştır?

A) Sayma sayıları 1 ile başlar.
B) Doğal sayılar sıfırdan başlar.
C) Tüm tam sayılar rasyonel sayıdır.
D) İrrasyonel sayılar kesir olarak yazılabilir.

9. Ardışık üç tek sayının toplamı 39’dur. En küçük sayı kaçtır?

A) 11
B) 12
C) 13
D) 14

10. Bir öğrenci, AYT deneme sınavında 4 farklı matematik kitabını sıralamak istiyor. Kaç farklı sıralama yapabilir?

A) 16
B) 20
C) 24
D) 28

Cevap Anahtarı

1. B
2. D
3. C
4. B
5. B
6. A
7. D
8. A
9. A
10. C