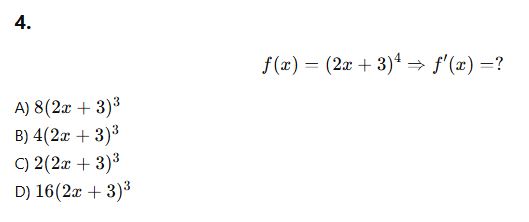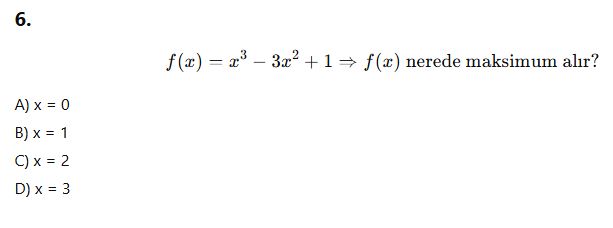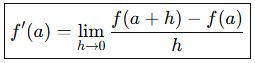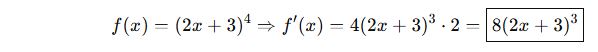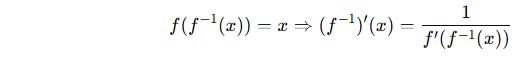AYT Matematik Türev Konu Anlatımı

Türev, bir fonksiyonun değişim hızını ve grafiğinin eğimini incelememizi sağlayan analiz konusudur.

AYT’de türev konusu;

• Türev tanımı ve geometrik yorumu

• Temel türev kuralları

• Fonksiyonların türevleri

• Türevle maksimum–minimum bulma

• Türevle artan–azalanlık, teğet eğimi ve grafik yorumu

• Uygulamalı problemler (hız, anlık değişim vb.)

başlıklarını içerir.

🔹 Ünitenin Alt Başlıkları:

1. Türev Kavramı ve Geometrik Yorum

2. Türev Alma Kuralları

3. Fonksiyonların Türevleri

4. Yüksek Mertebeden Türevler

5. Türevin Uygulamaları: Artan–Azalanlık

6. Türevin Uygulamaları: Ekstremum (maksimum–minimum)

7. Türevle Grafik ve Problem Çözümü

Türev Kavramı ve Geometrik Yorum

📘 A. Türev Nedir?

Türev, bir fonksiyonun bir noktadaki anlık değişim hızını veya o noktadaki teğetin eğimini verir.

Matematiksel Tanım:

​​

Bu ifade, x = a noktasındaki türevi verir.

📘 B. Türevin Geometrik Yorumu

• f′(a): Fonksiyonun x = a noktasındaki teğet eğimi

• Eğer f′(a) > 0: Fonksiyon o noktada yukarı eğimli

• Eğer f′(a) < 0: Fonksiyon o noktada aşağı eğimli

• Eğer f′(a) = 0: Fonksiyon o noktada teğet eksene paralel (zirve/dip olabilir)

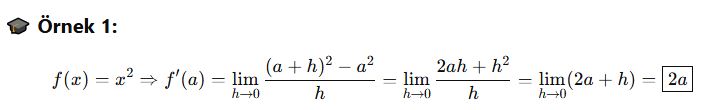
📘 C. Ortalama Hız – Anlık Hız

• Ortalama değişim:
  ​

• Anlık değişim:
  

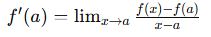
📘 D. Türev Var mı? Sürekli mi?

• Türev tanımı için fonksiyonun sürekli olması gerekir, ama her sürekli fonksiyon türevlenebilir olmayabilir

Türev Alma Kuralları

📘 A. Temel Türev Kuralları

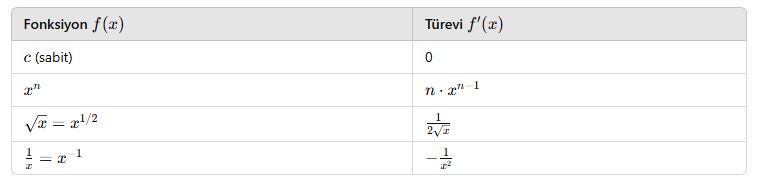
📘 B. Sabit Çarpan Kuralı

📘 C. Toplam / Fark Kuralı

🎓 Örnek 1:

🎓 Örnek 2:

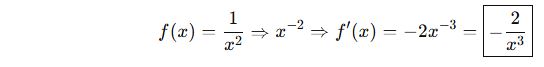
📘 D. Türev Alma Kuralları – Özelleştirilmiş Halleri

Fonksiyonların Türevleri

📘 A. Çarpım Kuralı

İki fonksiyonun çarpımının türevi:

​

🎓 Örnek 1:

​

📘 B. Bölüm Kuralı

İki fonksiyonun bölümünün türevi:

​​

🎓 Örnek 2:

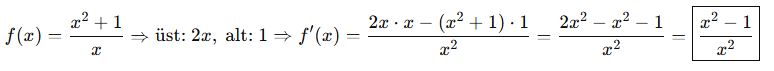
📘 C. Zincir (Bileşik Fonksiyon) Kuralı

Eğer

🎓 Örnek 3:

​

📘 D. Ters Fonksiyonun Türevi

​

Bu bilgi genelde ileri düzeyde çıkar, ama grafiksel yorum sorularında önemlidir.

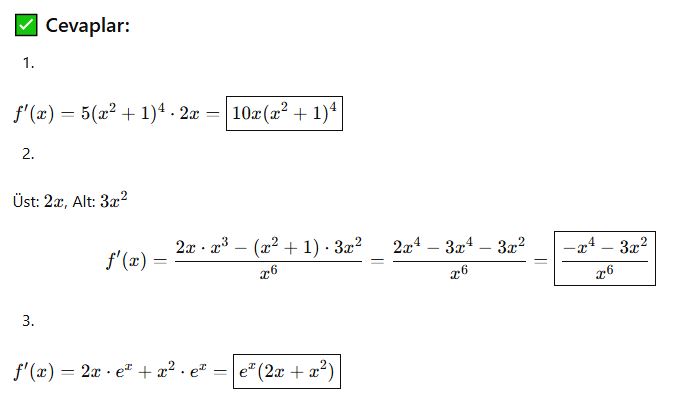
Yüksek Mertebeden Türevler

📘 A. Tanım

Bir fonksiyonun türevini aldıktan sonra, tekrar türevini alırsak bu yeni türeve ikinci türev denir.
Aynı şekilde, tekrar türev alınarak üçüncü, dördüncü… türevlere geçilir.

📘 Gösterim:

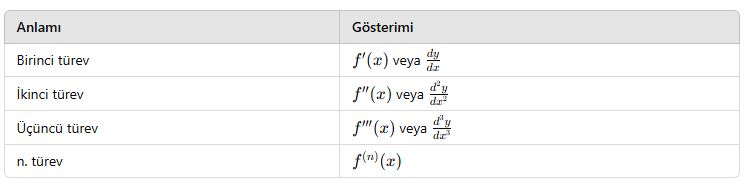
📘 B. Anlamı Nedir?

• f′(x): fonksiyonun hızını, eğimini verir

• f′′(x): fonksiyonun ivmesini, yani eğimin değişim hızını verir

• f′′(x)>0: çukur yukarı (konkav),

• f′′(x)<0: çukur aşağı

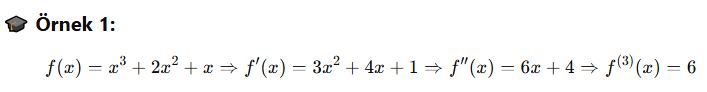
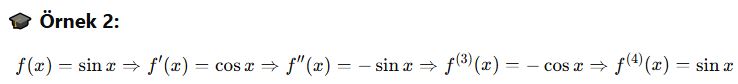
Trigonometrik fonksiyonların türevleri periyodik olarak döner.

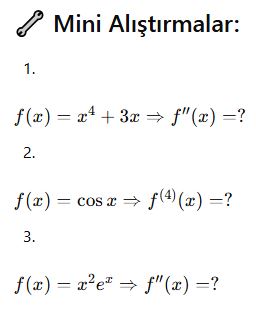
Türevin Uygulamaları – Artan ve Azalan Fonksiyonlar

📘 A. Artan ve Azalan Fonksiyon Nedir?

Bir fonksiyonun bir aralıkta nasıl davrandığını türev yardımıyla inceleyebiliriz:

📘 B. İşaret Tablosu ile İnceleme

1. f′(x) bulunur

2. İşaret değişim noktaları (kökler) belirlenir

3. Aralıklar seçilir ve işaretler yazılır

4. Fonksiyonun davranışı yorumlanır

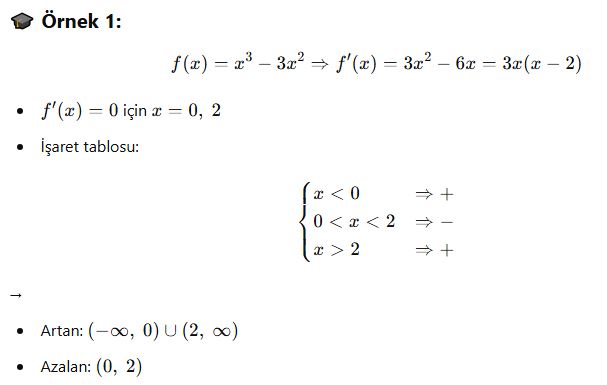
📘 C. Grafik Yorumu

• f′(x)>0: Grafik yukarı çıkıyor

• f′(x)<0: Grafik aşağı iniyor

• f′(x)=0: Grafik o noktada teğet, yön değiştiriyor olabilir

Türevin Uygulamaları – Maksimum ve Minimum (Ekstremum) Değerler

📘 A. Ekstremum Nedir?

Bir fonksiyonun yerel en büyük (maksimum) ya da yerel en küçük (minimum) değeri aldığı noktaya ekstremum noktası denir.

Bu noktalar genelde türev kullanılarak bulunur.

📘 B. Nasıl Bulunur?

1. Fonksiyonun türevi alınır: f′(x)

2. Türev sıfır yapılır: f′(x)=0 çözülür

3. Bulunan $x$ değerleri kritik noktalardır

4. İşaret tablosuyla incelenir:

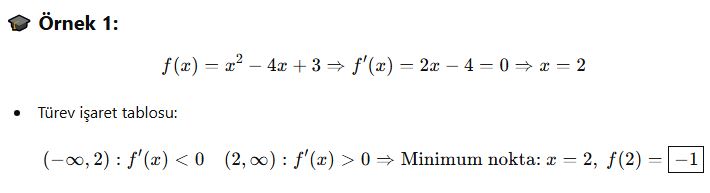
📘 C. Uygulama: Alan, Kâr, Hacim Problemleri

Türevle maksimum–minimum sorularında şu kavramlar sık gelir:

• En kısa tel → minimum uzunluk

• Maksimum alan

• En yüksek kâr

• Hacmi en büyük kutu

• En kısa/uzun mesafe

Türevle Grafik ve Problem Yorumları

📘 A. Türev ve Grafiğin İlişkisi

Bir fonksiyonun grafiği verildiğinde, o fonksiyonun türev grafiğiyle:

• Artanlık ↔ f′(x) > 0

• Azalanlık ↔ f′(x) < 0

• Tepe/dip ↔ f′(x) = 0

• Maksimum/minimum noktalarda türev işaret değiştirir

📘 B. Türev Grafiği Verilirse Fonksiyon Yorumu

Ters analiz de mümkündür:
Eğer f′(x) grafiği veriliyorsa:

• f′(x) > 0 → f(x) artan

• f′(x) < 0 → f(x) azalan

• f′(x) = 0 ve işaret değişiyorsa → ekstremum noktası

🎓 Örnek 1:

Fonksiyonun grafiğinde:

• x = 1’de eğim pozitif

• x = 2’de yatay teğet

• x = 3’ten sonra azalan

Yorum:

• Artan: (–∞, 2)

• Azalan: (2, ∞)

• x = 2’de maksimum

• f′(2)=0

📘 C. Uygulamalı Problem Yorumları

Türev, sadece grafik değil aynı zamanda hareket, maliyet, kar, hız gibi birçok uygulamalı problemin çözümünde kullanılır.

Örnek Problem 1:

Bir cismin konumu:

• Cismin hızı 0 olan anlar:

• t = 1’de hız yön değiştiriyorsa → durma ve yön değiştirme vardır

Örnek Problem 2:

Bir kar üreticisinin maliyet fonksiyonu:

• Maliyet en düşük ne zaman?
  ​

AYT Türev Deneme Testi

(Cevap anahtarı en altta)