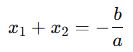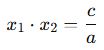TYT Matematik 2.Dereceden Denklemler Konu Anlatımı

Matematikte ikinci dereceden denklemler, en temel ve en yaygın kullanılan denklem türlerinden biridir. Bu tür denklemler, kareli bir değişken içeren ve standart formda yazılabilen denklemler olarak bilinir.

Genel olarak ikinci dereceden bir bilinmeyenli denklem, şu şekilde ifade edilir:

Burada:

İkinci dereceden denklemler mühendislik, ekonomi, fizik ve birçok bilim dalında yaygın olarak kullanılır.

Bu ünitede, ikinci dereceden denklemleri ve çözüm yöntemlerini detaylı bir şekilde ele alacağız.

İkinci Dereceden Bir Bilinmeyenli Denklem

İkinci dereceden bir bilinmeyenli denklem, değişkenin en yüksek derecesi 2 olan ve tek bir bilinmeyen içeren cebirsel denklemdir.

1. Genel Formu

Bir ikinci dereceden bir bilinmeyenli denklem, şu şekilde yazılır:

Burada:

• x, bilinmeyen değişkendir.
• a,b,c katsayıları gerçek sayılar olmak zorundadır.
• Önemli: a≠0 olmalıdır. Eğer a=0 olursa, denklem ikinci dereceden olmaktan çıkar ve birinci dereceden bir denklem haline gelir.

2. İkinci Dereceden Denklemlere Örnekler

✅ İkinci dereceden denklemler:

❌ İkinci dereceden olmayan denklemler:

3. Katsayıların Özellikleri ve Önemi

4. İkinci Dereceden Denklemlerin Grafiği

Bir ikinci dereceden denklem, parabol adı verilen bir eğriyi temsil eder.

• Eğer a>0 ise, parabol yukarı doğru açılır.
• Eğer a<0 ise, parabol aşağı doğru açılır.

Örnek grafik:

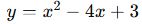•   denklemi bir paraboldür ve çözüm noktaları (parabolün x-eksenini kestiği noktalar) denklemin kökleridir.

İkinci Dereceden Denklemlerin Çözüm Kümesi

Bir ikinci dereceden bir bilinmeyenli denklemin çözüm kümesi, denklemi sağlayan $x$ değerlerinden oluşur. Bu çözüm kümeleri, denklemin kökleri olarak da adlandırılır.

1. İkinci Dereceden Denklemlerin Çözüm Kümesi Nedir?

Genel formdaki bir ikinci dereceden denklem:

eşitliği sağlayan x değerleri, bu denklemin çözüm kümesini oluşturur.

• Bir ikinci dereceden denklemin en fazla 2 farklı kökü olabilir.
• Kökler gerçek sayılar veya karmaşık sayılar olabilir.
• Kökler çarpanlara ayırma, tam kareye tamamlama veya diskriminant (delta) yöntemiyle bulunur.

2. Örnek Çözüm Kümesi Belirleme

Örnek 1:

Örnek 2:

Örnek 3: (Tam Kare Denklem)

İkinci Dereceden Denklemlerin Çözümü

İkinci dereceden denklemleri çözmek için farklı yöntemler kullanabiliriz. Kullanılacak yöntem, denklemin yapısına bağlıdır. En yaygın çözüm yöntemleri şunlardır:

1. Çarpanlara Ayırma Yöntemi
2. Tam Kareye Tamamlama Yöntemi
3. İkinci Dereceden Denklem Formülü (Deltalı Yöntem – Diskriminant Yöntemi)
4. Değişken Değiştirme Yöntemi

Şimdi her bir yöntemi detaylıca ele alalım.

1. Çarpanlara Ayırma Yöntemiyle Çözüm

Eğer ikinci dereceden denklem çarpanlarına ayrılabiliyorsa, en hızlı ve kolay çözüm yolu budur.

2. Tam Kareye Tamamlama Yöntemiyle Çözüm

Çarpanlara ayrılamayan bazı ikinci dereceden denklemleri tam kareye tamamlayarak çözebiliriz.

3. İkinci Dereceden Denklem Formülü (Diskriminant – Delta Yöntemi)

Herhangi bir ikinci dereceden denklem:

4. Değişken Değiştirme Yöntemi

Bazı denklemler direkt ikinci dereceden olmayabilir, ancak değişken değiştirerek ikinci dereceden denklem haline getirilebilirler.

İkinci Dereceden Denklemleri Çarpanlarına Ayırma

İkinci dereceden denklemleri çözmenin en hızlı ve etkili yollarından biri, çarpanlara ayırma yöntemidir. Bu yöntemde, denklemi çarpım halinde yazıp sıfıra eşitleyerek kökleri buluruz.

1. Çarpanlara Ayırma Yöntemiyle Çözüm

Eğer ikinci dereceden denklem şu formda verildiyse:

2. Çarpanlara Ayırma Adımları

Bir denklemi çarpanlarına ayırmak için şu adımları izleriz:

1. Çarpımları sabit terimi (c) veren ve toplamları orta terimin katsayısı (b) olan iki sayı bulunur.
2. Denklem, bu sayılar kullanılarak iki çarpanın çarpımı şeklinde yazılır.
3. Her bir çarpan sıfıra eşitlenerek kökler bulunur.

3. Örnekler ve Çözümleri

Örnek 2: Çarpanlara Ayırma – Ortak Çarpan Parantezine Alma

Örnek 3: Çarpanlara Ayırma – İki Kare Farkı

Örnek 4: Çarpanlara Ayırma – Katsayıları Büyük Denklemler

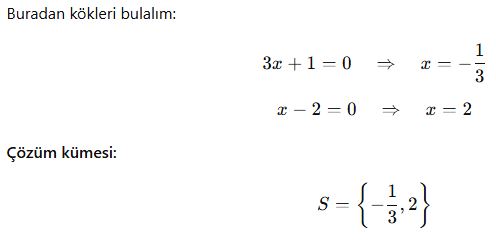
4. Çarpanlara Ayırmanın Kullanıldığı Diğer Durumlar

✅ Tam Kare İfadeler:
Eğer ikinci dereceden denklem tam kare şeklindeyse, şu formda yazılabilir:

Buradan tek bir kök çıkar.

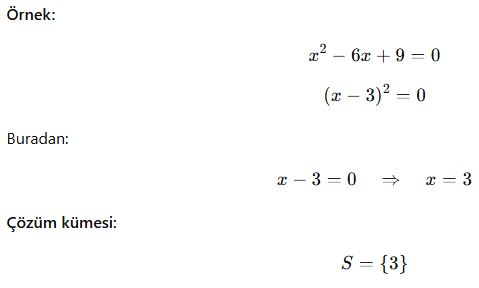
Çarpanlara Ayırma Yöntemleri

İkinci dereceden denklemleri çözmek için çarpanlara ayırma en etkili yöntemlerden biridir. Çarpanlara ayırma, ifadeyi daha küçük çarpanlara bölerek çözüm bulmayı kolaylaştırır. Farklı durumlara göre kullanılan başlıca çarpanlara ayırma yöntemleri şunlardır:

1. Ortak Çarpan Parantezine Alma
2. İki Kare Farkı
3. Tam Kare İfadeler
4. Çarpım ve Toplam Yöntemi
5. Gruplama Yöntemi
6. Değişken Değiştirme Yöntemi

Şimdi her bir yöntemi detaylı inceleyelim.

1. Ortak Çarpan Parantezine Alma

Eğer bir ifadede tüm terimlerde ortak bir çarpan varsa, bu çarpanı parantez dışına alarak ifadeyi sadeleştirebiliriz.

2. İki Kare Farkı

Matematikte iki kare farkı şu formülle ifade edilir:

3. Tam Kare İfadeler

Eğer bir denklem tam kare açılımı şeklindeyse, şu formüller kullanılır:

4. Çarpım ve Toplam Yöntemi

5. Gruplama Yöntemi

Eğer bir ikinci dereceden denklem çarpanlara doğrudan ayrılamıyorsa, gruplama yöntemi uygulanabilir.

6. Değişken Değiştirme Yöntemi

Bazı denklemler doğrudan ikinci dereceden olmayabilir, ancak değişken değiştirme yöntemi ile ikinci dereceden hale getirilebilirler.

Tam Kare İfadeler

Tam kare ifadeler, bir ifadenin karesi şeklinde yazılabilen özel polinomlardır. Bu ifadeler, ikinci dereceden denklemleri çarpanlarına ayırma ve çözme süreçlerinde sıkça kullanılır.

1. Tam Kare İfadelerin Tanımı

Bir ikinci dereceden ifade şu şekilde yazılabiliyorsa, tam kare ifadedir:

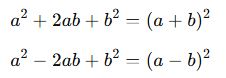
Bu tür ifadeler tam kare üçlüleri olarak adlandırılır.

2. Tam Kare Açılımları

Pozitif (Toplam İçeren) Tam Kare Açılımı:

Negatif (Fark İçeren) Tam Kare Açılımı:

Örnekler:

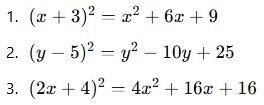
3. Tam Kare Olduğunu Anlama

Bir ikinci dereceden ifade tam kare mi, değil mi? Bunu anlamak için şu adımları takip edebiliriz:

Adım 1: İlk terimin karekökünü alın.
Adım 2: Son terimin karekökünü alın.
Adım 3: Orta terimi kontrol edin: 2ab formunda mı?

Örnek 1:

4. Tam Kareye Tamamlama Yöntemi

Bazen ikinci dereceden denklemleri çözmek için tam kareye tamamlama yöntemi kullanılır. Bu yöntemde, eksik olan tam kare terimi eklenerek ifade tam kare haline getirilir.

5. Tam Kare Olmayan Bir İfade Nasıl Tam Kare Yapılır?

Eğer elimizde tam kare olmayan bir ifade varsa, bunu tam kareye tamamlayarak çözebiliriz.

3 Terimli İfadeler (Trinomlar)

İkinci dereceden denklemler genellikle 3 terimli ifadeler (trinomlar) içerir. Bu tür ifadeleri çarpanlarına ayırarak veya tam kareye tamamlayarak çözebiliriz.

1. 3 Terimli İfadelerin Tanımı

Bir polinom, üç terimli bir ifade (trinom) ise şu şekilde yazılır:

2. 3 Terimli İfadeleri Çarpanlara Ayırma

Bir trinom çarpanlarına ayrılabiliyorsa, iki çarpan halinde yazılabilir:

3. Katsayısı 1’den Farklı Olan Trinomlar

4. Tam Kare 3 Terimli İfadeler

Eğer bir trinom tam kare şeklindeyse, şu formlara sahiptir:

Örnek 3: Tam Kare Trinom

Tam Kareye Tamamlama Yöntemi

Tam kareye tamamlama, ikinci dereceden denklemleri çözmek için kullanılan etkili bir yöntemdir. Bu yöntem özellikle çarpanlara ayrılamayan denklemleri çözmede ve ikinci dereceden fonksiyonların tepe noktasını bulmada kullanılır.

1. Tam Kareye Tamamlama Yönteminin Mantığı

Genel ikinci dereceden denklem:

2. Tam Kareye Tamamlama Adımları

Daha iyi anlamak için örnekler üzerinden inceleyelim.

3. Katsayısı 1’den Farklı Olan Denklemler

4. Tam Kareye Tamamlama Kullanım Alanları

• İkinci dereceden denklemleri çözmek
• Parabolün tepe noktasını bulmak
• Denklemleri grafik üzerinde incelemek
• Fizik ve mühendislik problemlerinde optimizasyon

Değişken Değiştirme Yöntemi

Değişken değiştirme yöntemi, çözümü zor görünen ikinci dereceden denklemleri daha basit bir forma getirmek için kullanılan bir tekniktir. Bu yöntem, bilinmeyen değişkenin yerine başka bir değişken koyarak denklemi daha basit bir hale getirmeyi amaçlar.

1. Değişken Değiştirme Yöntemi Nedir?

Bir denklemde belirli bir ifadeyi başka bir değişkenle (örneğin y ile) değiştirerek denklemi standart ikinci dereceden denklem formuna getirebiliriz.

Genellikle şu tip denklemlerde kullanılır:

2. Üslerin Katlarını İçeren Denklemler

3. Trigonometrik Denklemler İçin Değişken Değiştirme

Bazen sinüs, kosinüs veya tanjant içeren ikinci dereceden denklemler de değişken değiştirme yöntemiyle çözülür.

4. Üstel Fonksiyonlarda Değişken Değiştirme

Bazen üstel ifadeleri içeren denklemler değişken değiştirme yöntemiyle çözülebilir.

5. Karmaşık Sayıları İçeren Denklemler

Bazen değişken değiştirme yöntemi ile karmaşık sayılar da içeren çözümler elde edilebilir.

Özet: Ne Zaman Değişken Değiştirme Kullanmalıyız?

✅ Üslerin katları olduğunda (örneğin  gibi)
✅ Trigonometrik ifadeler içerdiğinde
✅ Üstel ifadelerde
✅ Karmaşık sayılarla çözüm gerektirdiğinde

İkinci Dereceden Denklemlerin Diskriminantı (Deltası)

Diskriminant (Δ), ikinci dereceden bir denklemin kökleri hakkında bilgi veren önemli bir ifadedir. Köklerin sayısını ve türünü belirlemek için kullanılır.

1. Diskriminant (Delta) Nedir?

Bir ikinci dereceden denklem şu formdadır:

2. Diskriminant Kullanarak Köklerin Türünü Belirleme

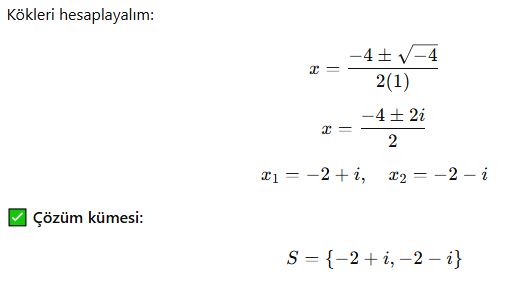
3. Diskriminantın Grafikte Yorumu

Diskriminant değeri, parabolün x-eksenini kesme durumunu belirler:

• Δ>0: Parabol x-eksenini iki farklı noktada keser.
• Δ=0: Parabol x-eksenine teğettir (tek bir noktada dokunur).
• Δ<0: Parabol x-eksenini kesmez, kökler karmaşıktır.

Özet: Diskriminant ve Köklerin Durumu

Δ (Delta) Sıfırdan Büyükse (Δ > 0) Durumu

Eğer diskriminant (Δ) sıfırdan büyükse, ikinci dereceden denklemin iki farklı gerçek kökü vardır. Bu durumda, parabol x-eksenini iki farklı noktada keser.

3. Grafikte Δ > 0 Durumunun Yorumu

Eğer Δ > 0 ise:

• Parabol x-eksenini iki farklı noktada keser.
• İki farklı reel kök vardır.
• Parabol ya yukarı ya da aşağı doğru açılır (a’nın işaretine bağlı olarak).

📌 Grafik yorumları:

• Eğer a>0 ise: Parabol yukarı açılır ve x-eksenini iki noktada keser.
• Eğer a<0 ise: Parabol aşağı açılır ve x-eksenini iki noktada keser.

4. Genel Özet

Δ (Delta) Sıfırsa (Δ = 0) Durumu

Eğer diskriminant (Δ) sıfıra eşitse, ikinci dereceden denklem çakışık (çift katlı) bir köke sahiptir. Bu durumda, parabol x-eksenine teğet geçer ve tek bir reel kök bulunur.

Burada:

• Tek bir kök vardır.
• Kök çift katlıdır (çakışık kök denir).
• Parabol x-eksenine sadece bir noktada teğet geçer.

3. Grafikte Δ = 0 Durumunun Yorumu

Eğer Δ = 0 ise:

• Parabol x-eksenine teğet geçer.
• Tek bir reel kök vardır (çift katlı kök).
• Parabol sadece bir noktada x-eksenine dokunur, ekseni iki noktada kesmez.

📌 Grafik yorumları:

• Eğer a>0 ise: Parabol yukarı açılır ve x-eksenine teğet geçer.
• Eğer a<0 ise: Parabol aşağı açılır ve x-eksenine teğet geçer.

4. Genel Özet

Δ (Delta) Sıfırdan Küçükse (Δ < 0) Durumu

Eğer diskriminant (Δ) sıfırdan küçükse, ikinci dereceden denklem gerçek köke sahip değildir. Bunun yerine karmaşık (kompleks) kökler ortaya çıkar.

Bu durumda parabol x-eksenini kesmez ve çözüm kümesi karmaşık sayılar kümesindedir.

3. Grafikte Δ < 0 Durumunun Yorumu

Eğer Δ < 0 ise:

• Parabol x-eksenini kesmez.
• Gerçek kök yoktur, kökler karmaşıktır.
• Parabol tamamen x-ekseninin üstünde veya altında kalır.

📌 Grafik yorumları:

• Eğer a>0 ise: Parabol x-ekseninin üstünde kalır.
• Eğer a<0 ise: Parabol x-ekseninin altında kalır.

4. Genel Özet

İkinci Dereceden Denklemlerde Kök-Katsayı İlişkisi

İkinci dereceden denklemin kökleri ile katsayıları arasında belirli matematiksel ilişkiler vardır. Kökler toplamı ve kökler çarpımı, bu ilişkilerin en önemli olanlarıdır.

Genel formdaki bir ikinci dereceden denklem:

Bu denklemde kökler x1​ ve x2​ olarak adlandırılır. Kökler, şu formülle hesaplanır:

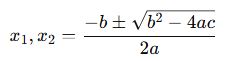
Bu kökler katsayılarla şu şekilde ilişkilidir:

1. Kökler Toplamı (Vieta Teoremi):

   ​

2. Kökler Çarpımı:

   ​

Bu iki formül, ikinci dereceden denklemleri çözümlemeden kökleri ve katsayılar arasındaki ilişkileri belirlememize yardımcı olur.

1. Kökler Toplamı ve Çarpımı Kullanarak Denklemin Bulunması

Eğer kökler x1 ve x2​ biliniyorsa, denklem şu şekilde yazılır:

Örnek 2: Katsayılardan Kökler Bulma

Bu bilgilerle çarpanlara ayırmadan köklerin toplamı ve çarpımı hakkında fikir sahibi olabiliriz.

3. Kökler Toplamı ve Çarpımı Kullanarak Sorular Çözme

Örnek 3: Bilinmeyen Katsayıyı Bulma

4. Özel Kök İlişkileri

a) Köklerin Çarpmaya Göre Terslerinin Toplamı

b) Kökler Farkı

Köklerin farkı, diskriminant (Δ) kullanılarak hesaplanır:

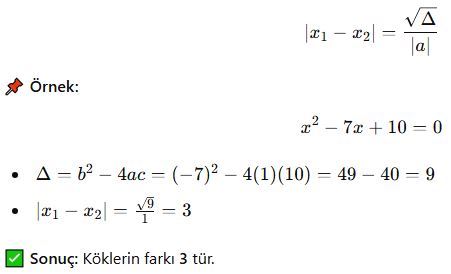
c) Simetrik Köklerde Kökler Toplamı

✅ Simetrik köklerde kökler toplamı her zaman sıfırdır.

5. Özet Tablo

Kökleri Bilinen Denklemin Yazılması

Eğer bir ikinci dereceden denklemin kökleri verilmişse, bu köklere göre denklem oluşturabiliriz. Bunu yapmak için kök-katsayı ilişkisini kullanırız.

1. Kökleri Bilinen Denklemin Genel Formülü

Eğer bir ikinci dereceden denklemin kökleri x1x_1x1​ ve x2x_2x2​ olarak verilmişse, bu köklere sahip olan denklem şu formda yazılabilir:

Bu çarpımı açarak standart ikinci dereceden denklem formuna dönüştürebiliriz:

Eğer katsayılar arasında bir çarpan k (pozitif veya negatif sabit) varsa, denklemi şu şekilde genelleştirebiliriz:

Bu formül, verilen köklerden ikinci dereceden denklemi oluşturmamıza yardımcı olur.

3. Kökleri Bilinen Özel Durumlar

• Eğer kökler eşitse (çift katlı kök), denklem şu formda yazılır:

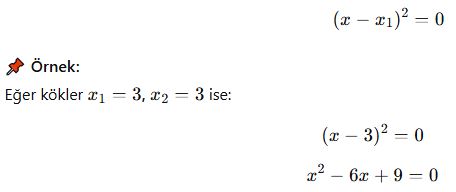
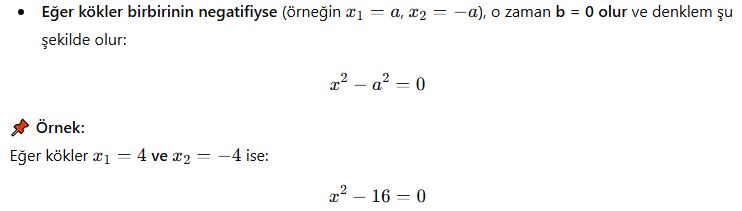
4. Özet Tablo

İKİNCİ DERECEDEN DENKLEMLER TESTİ

1. Aşağıdaki ifadelerden hangisi ikinci dereceden bir denklemdir?

2. Aşağıdaki denklemlerden hangisinin iki farklı gerçek kökü vardır?

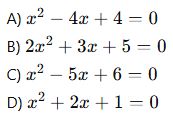
5. Diskriminantı sıfır olan ikinci dereceden bir denklemin kökleri nasıldır?

A) İki farklı gerçek kökü vardır.
B) Karmaşık kökleri vardır.
C) Tek bir çakışık (çift katlı) kökü vardır.
D) Kökü yoktur.

Bu test, İkinci Dereceden Denklemler konusunu kavramanızı pekiştirecek!