İçindekiler
TYT Matematik Çarpanlara Ayırma
Matematikte çarpanlara ayırma, ifadeleri daha küçük bileşenlere ayırarak sadeleştirme ve işlem kolaylığı sağlama yöntemidir. Özellikle polinomlarla ve cebirsel ifadelerle çalışırken büyük öneme sahiptir. TYT Matematik’te öğrencilerin çarpanlara ayırma becerisi kazanması, hem temel matematik işlemlerinde hız kazanmalarına hem de denklem çözme süreçlerinde daha sistemli bir yaklaşım benimsemelerine yardımcı olur.
Çarpanlara ayırma, farklı yöntemler kullanılarak gerçekleştirilebilir. En temel yöntemlerden biri ortak paranteze alma iken, daha ileri düzeyde özdeşlikler ve polinom bölmesi gibi teknikler de kullanılır. Bu konunun iyi anlaşılması, ilerleyen konular olan polinomlar, fonksiyonlar ve limit gibi alanlarda daha rahat işlem yapmayı sağlar. Bu bölümde çarpanlara ayırmanın temel tekniklerini detaylı bir şekilde inceleyecek ve örneklerle pekiştireceğiz.
Ortak Parantez Alma
Ortak Parantez Alma Nedir?
Ortak parantez alma, bir cebirsel ifadede ortak çarpanı belirleyerek terimleri daha sade bir biçime dönüştürme yöntemidir. Çarpanlara ayırma konusunun en temel adımıdır ve birçok matematiksel işlemin kolaylaştırılmasına yardımcı olur.
Bir cebirsel ifadede ortak olan sayıları veya değişkenleri parantez dışına çıkararak ifadeyi daha kompakt bir hale getiririz. Örneğin;
![]()
Burada, a ortak çarpan olduğu için parantez dışına alınmıştır.
Ortak Parantez Alma Yöntemleri
Ortak parantez alma işlemini uygularken şu adımları takip edebiliriz:
- Tüm terimlerde ortak olan sayıyı veya harfi belirle.
- Bu ortak çarpanı parantez dışına çıkar.
- Parantez içine geri kalan ifadeyi yaz.



Özel Durumlar
- Eğer bir ifadede tüm terimlerde ortak bir çarpan yoksa, farklı gruplamalar kullanılarak çarpanlara ayırma denenebilir. Bunu “Gruplara Ayırma” yönteminde detaylandıracağız.
- Bazen tüm terimlerde bir değişken bulunmayabilir, bu durumda sadece sayılar üzerinden ortak parantez alma işlemi yapılabilir.
Gruplara Ayırma
Gruplara Ayırma Nedir?
Gruplara ayırma yöntemi, ortak çarpan bulunamayan dört veya daha fazla terimli ifadeleri iki veya daha fazla gruba bölerek çarpanlara ayırma tekniğidir. Bu yöntemde ifadeyi uygun şekilde bölüp, her gruptan ortak çarpanı parantez dışına alarak işlemi tamamlarız.
Bu yöntemi şu adımlarla uygularız:
- Terimleri mantıklı bir şekilde iki gruba ayır.
- Her gruptaki ortak çarpanı parantez dışına al.
- Ortak parantez elde edildiyse, bu ifadeyi de ortak paranteze alarak işlemi tamamla.
Gruplara Ayırma Yöntemine Örnekler
Örnek 1:



Özet:
- Eğer ifadede ortak çarpan doğrudan yoksa, terimleri gruplara ayırarak işlem yapılır.
- Her grupta ortak çarpan parantez dışına alınır.
- Son olarak, her iki terimde de ortak olan parantez dışına alınarak çarpanlara ayırma tamamlanır.
Terim Ekleme/Çıkarma
Terim Ekleme/Çıkarma Nedir?
Terim ekleme veya çıkarma yöntemi, çarpanlara ayırma işlemini doğrudan yapamadığımız durumlarda kullanılan bir tekniktir. Burada, ifadenin yapısını değiştirmeden belirli terimler ekleyerek veya çıkararak çarpanlara ayırma işlemi yapılır.
Bu yöntem özellikle bazı özel ifadeleri elde etmek için kullanılır. Amaç, ifadeyi bilinen özdeşlikler veya gruplara ayırma yöntemi ile çözülebilecek bir hale getirmektir.
Terim Ekleme/Çıkarma Yöntemine Örnekler



Özet:
- Eğer çarpanlara ayırma doğrudan yapılamıyorsa, uygun terimler eklenip çıkarılarak çarpanlara ayrılabilir.
- Gruplama veya bilinen özdeşlikler kullanılarak ifade basitleştirilir.
- Tam kare ifadeler oluşturularak çarpanlara ayırma daha kolay hale getirilebilir.
Sadeleştirme
Sadeleştirme Nedir?
Sadeleştirme, verilen bir matematiksel ifadeyi en basit hâline getirmek için yapılan işlemdir. Çarpanlara ayırma sürecinin önemli bir parçasıdır çünkü ifadeleri mümkün olduğunca küçük parçalara bölmek, işlemleri daha kolay ve hızlı yapmamızı sağlar.
Bu yöntem özellikle kesirli ifadelerde, rasyonel ifadelerde ve polinomlarda yaygın olarak kullanılır. Çarpanlara ayırma tekniklerini kullanarak, pay ve paydayı ortak çarpanlarına ayırırız ve ardından sadeleştirme işlemi gerçekleştiririz.
Sadeleştirme Yöntemine Örnekler



Özet:
- Çarpanlara ayırma işlemi yaparak sadeleştirme gerçekleştirilir.
- Pay ve paydayı ortak çarpanlarına ayırarak ortak terimler sadeleştirilir.
- Kesirler sadeleştirildikten sonra daha basit hâle getirilir.
Özdeşlikler
Özdeşlik Nedir?
Özdeşlikler, matematikte her durumda doğru olan eşitliklerdir. Bu ifadeler, cebirsel işlemlerde çarpanlara ayırma ve sadeleştirme süreçlerini hızlandırmak için kullanılır. Özdeşlikleri bilmek, matematikte hızlı ve doğru işlem yapmamızı sağlar.
Özdeşlikler, özellikle çarpanlara ayırma konusunun temel taşlarından biridir. Çarpanlara ayırma işlemlerini yaparken bazı ifadeleri daha kısa yoldan parçalayabilmek için bu özdeşlikleri kullanırız.
Önemli Özdeşlikler
Matematikte sık kullanılan başlıca özdeşlikler şunlardır:
1. İki Kare Farkı Özdeşliği
![]()
Bu özdeşlik, iki sayının karelerinin farkı şeklinde olan ifadeleri çarpanlara ayırmak için kullanılır.
Örnek:
![]()
2. Tam Kare İfadeler
Tam kare ifadeler iki şekilde karşımıza çıkar:
- Pozitif terimli tam kare özdeşliği:
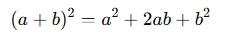
- Negatif terimli tam kare özdeşliği:
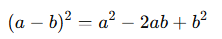
Bu özdeşlikler, bazı ifadeleri çarpanlarına ayırırken veya geliştirilmiş ifadeleri anlamak için kullanılır.
Örnek:

3. İki Küp Toplamı ve Farkı Özdeşlikleri
Bu özdeşlikler, küp ifadelerle işlem yaparken büyük kolaylık sağlar.
- İki küp toplamı:
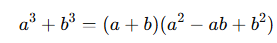
- İki küp farkı:
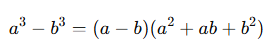
Örnek:
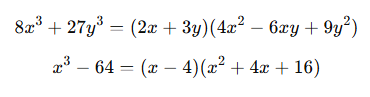
4. Üç Terimli İfadelerin Çarpanlara Ayrılması
Bazı üç terimli ifadeler özel durumlara sahiptir. Bunları çarpanlarına ayırırken deneme-yanılma veya özdeşlik bilgisi kullanılır.
Örneğin:
![]()
Çünkü 3 ve 4’ün çarpımı 12, toplamı 7 olduğu için bu şekilde çarpanlarına ayrılır.
Örnek Sorular ve Çözümleri


Özet:

İki Kare Farkı
İki Kare Farkı Nedir?
İki kare farkı, matematikte özel bir özdeşliktir ve şu şekilde ifade edilir:
![]()
Burada, a² ve b² birer tam kare olduğu sürece bu özdeşlik her zaman geçerlidir. İki kare farkı, özellikle çarpanlara ayırma işlemlerinde büyük kolaylık sağlar.
İki Kare Farkı Özdeşliğinin Kullanımı
Eğer verilen ifade iki tam kare terim içeriyorsa, bu terimleri (a – b) ve (a + b) biçiminde çarpanlara ayırabiliriz.
İki Kare Farkı Kullanımına Örnekler
Örnek 1:
![]()
ifadesini çarpanlarına ayıralım.
- 9, 3² olarak yazılabilir.
- Yani ifade şu hâle gelir:
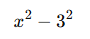
- İki kare farkı özdeşliğine göre:
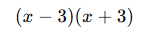
Sonuç:
![]()

Örnek 3:
![]()
ifadesini çarpanlarına ayıralım.
- x⁴, (x²)² olarak yazılabilir.
- 16, 4² olarak yazılabilir.
- Yani ifade şu hâle gelir:
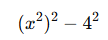
- İki kare farkı özdeşliğini uygularsak:
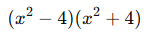
- Ancak, x² – 4 de iki kare farkıdır:
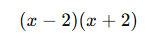
- Son hâli:
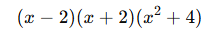
Sonuç:
![]()
Örnek 4:
![]()
ifadesini çarpanlarına ayıralım.
- 9x², (3x)² olarak yazılabilir.
- 49y², (7y)² olarak yazılabilir.
- Yani ifade şu hâle gelir:

Özet:
- İki kare farkı özdeşliği:

- Tam kare ifadeleri belirleyerek çarpanlara ayırırız.
- Çarpanlara ayırdıktan sonra gerekiyorsa yeniden iki kare farkı kontrol edilir.
- Özellikle büyük üslü ifadelerde tekrar eden iki kare farklarını unutma!
Tam Kare İfadeler
Tam Kare İfadeler Nedir?
Tam kare ifadeler, bir ifadenin bir binomun karesi olarak yazılabildiği durumları ifade eder. Yani, bir ifadenin tam kare olup olmadığını anlamak, çarpanlara ayırma işlemlerinde büyük kolaylık sağlar.
İki temel tam kare özdeşliği vardır:
- Pozitif terimli tam kare özdeşliği:
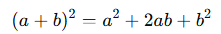
- Negatif terimli tam kare özdeşliği:
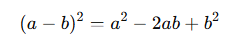
Bir ifadenin tam kare olup olmadığını belirlemek için:
- İlk ve son terimin tam kare olması gerekir.
- Ortadaki terimin, birinci ve üçüncü terimin kareköklerinin çarpımının iki katı olup olmadığı kontrol edilir.
Tam Kare İfadelerin Çarpanlara Ayrılması
Tam kare ifadeler, önce uygun binom özdeşlikleri kullanılarak çarpanlarına ayrılır.
Tam Kare İfadelere Örnekler






İki Küp Toplamı ve Farkı
İki Küp Toplamı ve Farkı Nedir?
Küp ifadelerin çarpanlara ayrılması, özel bir özdeşlik kullanılarak yapılır. İki kare farkı gibi, iki küp toplamı ve farkı da belirli formüllerle çarpanlara ayrılır.
İki küp toplamı ve farkı için aşağıdaki özdeşlikleri kullanırız:

İki Küp Toplamı ve Farkı Kullanımına Örnekler
Örnek 1:
![]()
ifadesini çarpanlarına ayıralım.
- 8, 2³ olarak yazılabilir.
- Yani ifade şu hâle gelir:
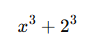
- İki küp toplamı özdeşliğine göre:
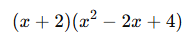
Sonuç:
![]()




Üç Terimli İfadelerin Çarpanlara Ayrılması
Üç Terimli İfadeler Nedir?
Üç terimli ifadeler, genellikle ikinci dereceden polinomlar olarak karşımıza çıkar ve çarpanlarına ayrılarak daha sade bir hale getirilebilir. Genel formu:
![]()
şeklindedir.
Üç terimli ifadelerin çarpanlara ayrılması için kullanılan yöntemler:
- Çarpanları bulma yöntemi (ax² + bx + c biçiminde)
- Gruplama yöntemi
- Tam kare ifadeleri kullanma
1. Çarpanları Bulma Yöntemi
Eğer a = 1 ise (yani x²’nin katsayısı 1 ise), çarpanlarına ayırmak için şunu yaparız:
- Toplamları b’yi veren,
- Çarpımları c’yi veren iki sayı bulunur.
Örnek 1:
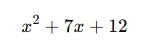
ifadesini çarpanlarına ayıralım.
- Çarpımları 12, toplamları 7 olan sayıları bulalım.
- Bu sayılar 3 ve 4’tür, çünkü 3 × 4 = 12 ve 3 + 4 = 7.
- O hâlde ifadeyi şu şekilde yazabiliriz:
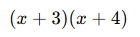
Sonuç:
![]()

2. Katsayılar Büyük Olduğunda Çarpanlara Ayırma
Eğer x²’nin katsayısı 1’den farklıysa (örneğin 2x² gibi), şu adımları izleriz:
- a × c çarpımını bul.
- Çarpımları a × c olan ve toplamları b olan iki sayı seç.
- Ortadaki terimi bu iki sayıya bölerek gruplama yap.
- Ortak paranteze alarak çarpanlara ayır.
Örnek 3:
![]()
ifadesini çarpanlarına ayıralım.

3. Tam Kare İfade Kullanarak Çarpanlara Ayırma
Eğer bir ifade tam kare şeklindeyse, onu tam kare açılımı olarak yazabiliriz.
Örnek 4:
![]()
ifadesini çarpanlarına ayıralım.
- x² = (x)^2 ve 9 = (3)^2

- Çarpanlarına ayırırsak:
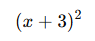
Sonuç:
![]()
Özet:
- Çarpanları bulma yöntemi ile üç terimli ifadeler çarpanlarına ayrılabilir.
- Eğer x²’nin katsayısı 1 değilse, gruplama yöntemi kullanılmalıdır.
- Tam kare ifadeler, özel formüllerle çarpanlarına ayrılabilir.
Polinom Bölmesi
Polinom Bölmesi Nedir?
Polinom bölmesi, bir polinomu başka bir polinoma bölme işlemi olarak tanımlanır. Bu işlem, uzun bölme yöntemi kullanılarak yapılır ve denklem çözme, çarpanlara ayırma ve polinomların sadeleştirilmesi gibi birçok alanda kullanılır.
Polinom bölmesi rasyonel ifadelerin sadeleştirilmesi ve polinomların çarpanlarına ayrılması için oldukça önemlidir.
Polinom Bölmesi Adımları
Uzun bölme yöntemini kullanarak P(x) polinomunu D(x) polinomuna bölerken aşağıdaki adımları takip ederiz:
- Bölünenin en büyük dereceli terimini, bölenin en büyük dereceli terimine böl.
- Çıkan sonucu bölenin tüm terimleriyle çarp ve bölünenden çıkar.
- Yeni elde edilen ifadede aynı işlemi tekrarla.
- Derecesi bölen polinomdan küçük bir kalan elde edene kadar işlemi sürdür.
Polinom Bölmesi Örnekleri
Örnek 1:
![]()
ifadesini uzun bölme yöntemiyle bölelim.

![]()

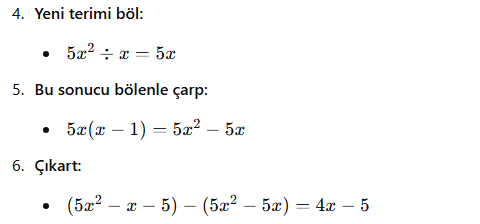
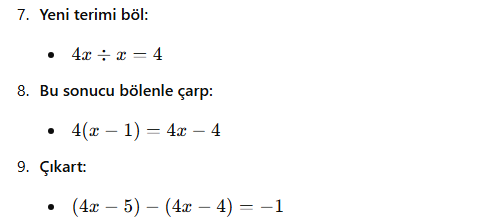
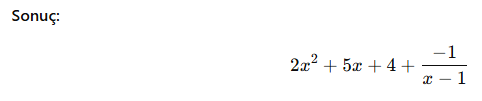
Polinom Bölmesinin Kullanım Alanları
- Rasyonel ifadeleri sadeleştirme
- Polinomları çarpanlara ayırma
- Denklem çözme
- Asimptotları bulma (grafik analizlerinde)
Özet:
- Polinom bölmesi, polinomları daha küçük ifadelere ayırmak için kullanılan bir yöntemdir.
- Bölme işlemi, en yüksek dereceli terimlerden başlanarak yapılır.
- Sonuç, bir polinom ve gerekirse bir kalan terimi içerir.
- Kalan sıfırsa, bölen polinom bölünenden bir çarpandır.
Rasyonel Kök Teoremi
Rasyonel Kök Teoremi Nedir?
Rasyonel Kök Teoremi, bir polinomun rasyonel köklerini (kesirli köklerini) belirlemek için kullanılan önemli bir yöntemdir. Polinom denklemlerinin köklerini tahmin etmeyi kolaylaştırır ve çarpanlara ayırma sürecinde büyük yardımcı olur.
Bir polinomun rasyonel kökü olup olmadığını ve eğer varsa hangi değerlerin aday olabileceğini belirlemek için aşağıdaki teoremi kullanırız:
Rasyonel Kök Teoremi:
Bir polinomun bütün rasyonel kökleri, şu formdaki sayılardan oluşur:
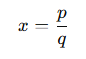
Burada:
- p, sabit terimin bölenleridir (polinomun en sağdaki sabit katsayısı).
- q, en yüksek dereceli terimin katsayısının bölenleridir.
Tüm olası rasyonel kökler, ![]() şeklinde yazılabilen tam sayı veya kesirli sayılardır.
şeklinde yazılabilen tam sayı veya kesirli sayılardır.
Rasyonel Kök Teoremi Kullanımına Örnekler
Örnek 1:
![]()

Kökleri Deneyelim:
- x = 2’yi deneyelim
![]()
- x = 2 bir köktür.
Bu durumda, x – 2 polinoma bir çarpandır. Geri kalan ifadeyi uzun bölme veya çarpanlara ayırma yöntemiyle çözeriz.
Örnek 2:
![]()

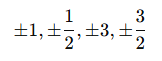
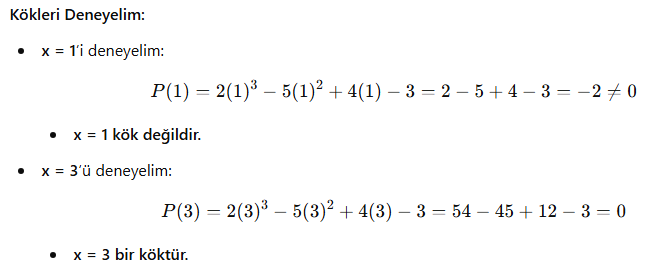
Bu durumda, x – 3 polinoma bir çarpandır. Geri kalan ifadeyi uzun bölme yöntemiyle çözebiliriz.



Özet:
- Rasyonel Kök Teoremi, bir polinomun rasyonel köklerini tahmin etmek için kullanılır.
- Kökler
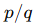 formatında bulunur, burada:
formatında bulunur, burada:
- p, sabit terimin bölenleri
- q, en büyük dereceli terimin bölenleridir.
- Olası rasyonel kökler tek tek denenerek sıfır yapan değerler bulunur.
- Bulunan kökler, polinomun çarpanlara ayrılmasına yardımcı olur.
TYT Matematik: Çarpanlara Ayırma Testi
1.Aşağıdaki ifadeyi çarpanlarına ayırınız:

2.Aşağıdaki ifadeyi çarpanlarına ayırınız:
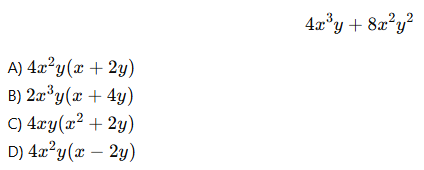
3.Aşağıdaki ifadeyi çarpanlarına ayırınız:
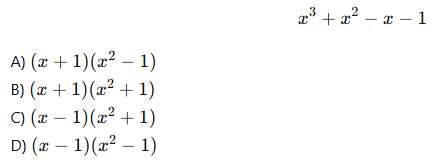
4.Aşağıdaki ifadeyi çarpanlarına ayırınız:
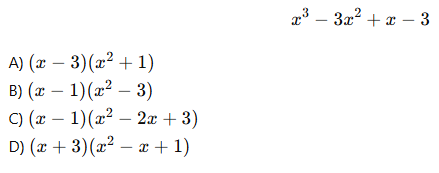
5.Aşağıdaki ifadeyi çarpanlarına ayırınız:
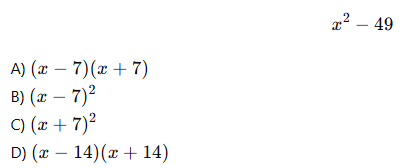
6.Aşağıdaki ifadeyi çarpanlarına ayırınız:
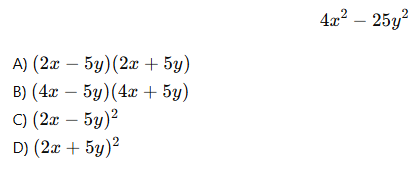
7.Aşağıdaki ifadeyi çarpanlarına ayırınız:

8.Aşağıdaki ifadeyi çarpanlarına ayırınız:




Cevap Anahtarı
- B
- A
- A
- C
- A
- A
- A
- A
- A
- A
- B
- A
Bu test, TYT Matematik Çarpanlara Ayırma konusunu kapsayıcı şekilde hazırlandı. Konuyu pekiştirmek için çözümleri detaylı inceleyebilirsin. 🎯

