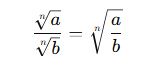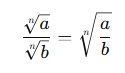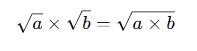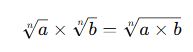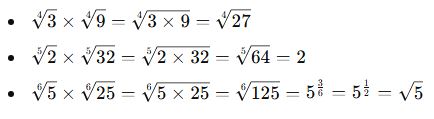TYT Matematik Köklü Sayılar Konu Anlatımı

Köklü sayılar, bir sayının tam sayı kuvvetleriyle ifade edilemediği durumlarda kullanılan matematiksel ifadelerdir. Bir sayıyı belirli bir derecede kök içinde göstermek, onu daha anlaşılır ve işlemler açısından daha pratik hale getirmemizi sağlar.

TYT Matematik sınavında köklü sayılar konusu oldukça önemlidir. Çünkü üslü ifadeler, denklemler, eşitsizlikler ve geometri gibi birçok alanda köklü sayılar kullanılmaktadır. Bu nedenle, köklü ifadeleri tanımak, işlemlerini bilmek ve nasıl kullanılacağını anlamak matematik başarınızı artıracaktır.

Bu ünitede köklü sayıların tanımını, özelliklerini, üslü ifadelerle ilişkisini, dört işlemleri, köklü denklemleri ve eşitsizlikleri detaylı bir şekilde ele alacağız. Her alt başlığı örneklerle destekleyerek konuyu en iyi şekilde anlamanızı sağlayacağız.

Şimdi köklü ifadelerle matematik yolculuğumuza başlayalım! 🚀📚

Köklü İfade Tanımı

Köklü sayılar, bir sayının belirli bir dereceden kökünün alınmasıyla elde edilen sayılardır. Matematikte bir sayının üssünün tersini almak anlamına gelir. Kareköklü sayılar en yaygın kullanılan köklü ifadelerdendir, ancak küp kök, dördüncü dereceden kök gibi farklı dereceler de bulunmaktadır.

Köklü İfadelerin Genel Gösterimi

Bir sayının köklü ifade olarak gösterimi şu şekildedir:

Burada;

Eğer kökün derecesi yazılmazsa, otomatik olarak 2. derece (kare kök) olduğu kabul edilir.

Köklü Sayıların Üslü Gösterimi

Köklü ifadeler üslü ifadelerle de yazılabilir:

Bu özelliği kullanarak köklü ifadeler ve üslü ifadeler arasındaki dönüşümleri daha kolay yapabiliriz.

Köklü Sayılarla Temel İşlemler

Köklü sayılar tam sayı çıkıyorsa rasyonel, çıkmıyorsa irrasyonel sayı olabilir.

Kök Derecesine Göre Köklü Sayılar

Köklü İfadelerin Değerini Bulma

Bir köklü ifadenin değerini bulmak, kök içindeki sayıyı tam sayı veya kesirli bir ifade olarak ifade etmek anlamına gelir. Köklü ifadeleri değerlendirirken tam kare sayılar, tam küp sayılar ve üslü sayı bilgisi oldukça önemlidir.

Kareköklü Sayıların Değerini Bulma

Bir sayının karekökü, kendisiyle çarpıldığında o sayıyı veren değerdir.

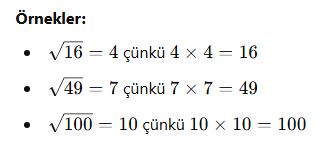
Tam Kare Olmayan Sayıların Yaklaşık Değerini Bulma

Tam kare olmayan sayılar irrasyonel sayı oldukları için yaklaşık değerlerini belirlemek gerekir.

Yaklaşık Değer Tablosu:

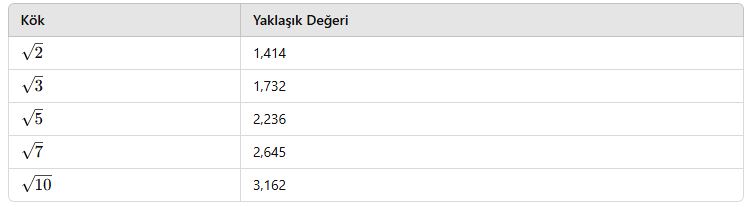
Bu değerleri bilmek, köklü sayılarla işlem yaparken hız kazandırır.

Küpkök ve Daha Yüksek Dereceden Köklerin Değerini Bulma

Bir sayının küpkökü, kendisiyle üç defa çarpıldığında o sayıyı veren değerdir.

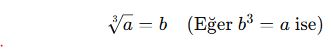
Kesirli (Rasyonel) Sayıların Kök Değerlerini Bulma

Kök içinde bir kesir varsa, hem pay hem payda ayrı ayrı kök içine alınabilir.

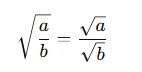
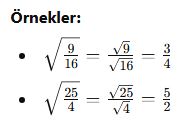
Köklü İfadelerin İçindeki Çarpanları Ayırarak Değer Bulma

Bazı köklü sayıları tam kare çarpanlarına ayırarak kök dışına çıkarmak mümkündür.

Özet:

• Tam kare olan köklü ifadeler tam sayı olarak çıkar.
• Tam kare olmayan köklü ifadeler yaklaşık değer ile ifade edilir.
• Kesirli köklü ifadeler hem pay hem paydaya ayrı ayrı kök uygulanarak çözülebilir.
• Çarpanları ayrılarak köklü sayılar sadeleştirilebilir.

Köklü İfadelerin Üslü İfadeye Dönüştürülmesi

Köklü ifadeleri üslü ifadelerle göstermek, işlem yapmayı kolaylaştıran bir yöntemdir. Özellikle çarpma, bölme, üstel kuvvet alma gibi işlemleri yaparken köklü sayıları üslü ifadeye dönüştürmek büyük avantaj sağlar.

Köklü İfadelerin Üslü Gösterimi

Bir n dereceden kök, üslü gösterimle şu şekilde ifade edilir:

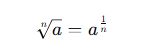
Bu kuralı tüm köklü ifadeler için uygulayabiliriz.

Kök İçindeki Üslü Sayıları Dönüştürme

Bir sayının üssü kök içinde bulunuyorsa şu şekilde dönüştürülür:

Bu özellik, köklü ifadelerle işlem yaparken büyük kolaylık sağlar.

Üslü İfadeleri Köklü Hale Getirme

Üslü ifadeleri tekrar köklü ifadeye çevirmek için üslerdeki kesirli ifadeyi kök olarak düşünebiliriz.

Bu dönüşüm, köklü ifadeleri anlamada ve işlemleri hızlandırmada yardımcı olur.

Üslü ve Köklü İfadelerle Çarpma ve Bölme

Çarpma İşlemi

Tabanları aynı olan üslü ifadeler çarpılırken üsler toplanır.

Ancak köklü ifadelerle işlem yaparken, önce üslü ifadeye çevirerek işlemi kolaylaştırabiliriz.

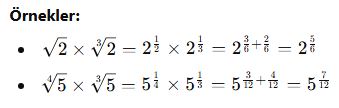
Bölme İşlemi

Tabanları aynı olan üslü ifadeler bölünürken üsler çıkarılır.

Bunu köklü ifadeler için de uygularız.

Üslü ve Köklü İfadelerde İşlem Önceliği

Matematikte işlem önceliği, köklü ve üslü ifadeler için de geçerlidir. İşlemler şu sırayla yapılmalıdır:

1. Parantez içindeki işlemler
2. Köklü ifadeler veya üs işlemleri
3. Çarpma ve bölme işlemleri
4. Toplama ve çıkarma işlemleri

Örnekler:

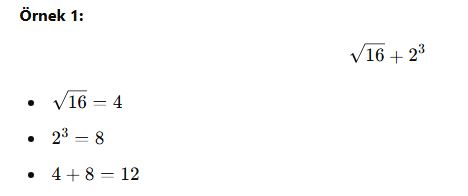
Özet:

✅ Köklü ifadeler üslü ifadeye dönüştürülebilir:

​

✅ Köklü ifadelerle çarpma ve bölme yaparken üsler toplanır veya çıkarılır.
✅ İşlem önceliğine dikkat edilmelidir.

Kök Derecesini Genişletme ve Sadeleştirme

Köklü ifadelerle işlem yaparken bazen kök derecesini genişletmek veya kökü sadeleştirmek gerekebilir. Bu işlemler, köklü sayılarla çarpma, bölme ve karşılaştırma yaparken hesaplamaları kolaylaştırır.

Kök Derecesini Genişletme

Bir köklü ifadeyi daha büyük bir derecede kök haline getirmek için şu kural kullanılır:

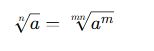
Bu formül, farklı derecelerdeki kökleri eşit bir kök derecesinde birleştirmek için kullanılır.

Kök Derecesini Sadeleştirme

Bir köklü ifadeyi daha küçük bir derecede yazabilmek için kökün derecesi ve üs arasında ortak bölen bulunur.

Genel Formül:

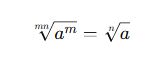
Eğer kök derecesi ve üs sadeleşebiliyorsa, en küçük hale getirilir.

Örnekler:

Farklı Kök Derecelerini Ortak Hale Getirme

Eğer işlemler sırasında farklı kök derecelerine sahip ifadeler varsa, bunları aynı kök derecesine getirerek işlem yapabiliriz.

Sonuç: Artık her iki ifade aynı kök içinde olduğu için sıralama ve işlemler daha kolay yapılabilir.

Kök Derecesini Genişletme ve Sadeleştirme İşlemlerinin Kullanım Alanları

Bu işlemler özellikle şu alanlarda işimize yarar:

✅ Çarpma ve bölme işlemlerinde kök derecelerini eşitlemek için
✅ Eşitsizlik veya sıralama yaparken ortak kök derecesine getirmek için
✅ Karmaşık köklü işlemleri sadeleştirmek için

Özet:

✅ Kök derecesini genişletme:

✅ Kök derecesini sadeleştirme:

✅ Farklı kök derecelerini eşitleyerek işlemler kolaylaştırılabilir.

Köklü Bir Sayıyı A√B Şeklinde Yazma

Köklü ifadelerle işlem yaparken bazen kök içindeki ifadeyi kök dışına çıkarmak gerekebilir. Bunun için köklü ifadeyi ​ şeklinde yazma yöntemi kullanılır. Bu yöntem, kök içindeki tam kare çarpanları ayırarak dışarı çıkarma prensibine dayanır.

Kök İçindeki Sayıyı Dışarı Çıkarma

Bir sayı tam kare bir çarpan içeriyorsa, bu çarpanı dışarı çıkarabiliriz.

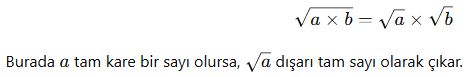
Örnekler:

Kök Dışına Çıkarma İşlemini Küpkök ve Daha Büyük Dereceli Kökler İçin Yapmak

Küpkök veya dördüncü dereceden kök gibi ifadelerde kök dışına çıkarma işlemi biraz farklıdır.
Eğer kök derecesi $n$ ise, sayıyı $n$. kuvvetli çarpanlarına ayırarak dışarı çıkarabiliriz.

Ters İşlem: Kök İçine Geri Gönderme

Eğer elimizde ​ gibi bir ifade varsa ve tekrar kök içine almak istiyorsak şu yöntemi kullanırız:

Neden Köklü Sayıları  Şeklinde Yazıyoruz?

🔹 İşlemleri kolaylaştırmak için:

🔹 Köklü sayılarla toplama ve çıkarma yapmak için:

• Aynı köklü terimleri birleştirerek işlemleri hızlandırırız.

🔹 Üslü işlemleri daha kolay yapmak için:

• ​ gibi ifadeleri tam kare ayırarak daha kolay çarpma ve bölme işlemi yapabiliriz.

Özet:

✅ Köklü ifadeleri ​ formuna getirmek, işlemleri kolaylaştırır.
✅ Tam kare çarpanları ayırarak kök dışına çıkarmak temel tekniktir.
✅ Daha yüksek dereceli köklerde tam küp veya dördüncü dereceden çarpanlara ayırarak dışarı çıkarma yapılabilir.
✅ İfade tekrar kök içine alınabilir.

Köklü Sayılarda Toplama ve Çıkarma İşlemi

Köklü sayılarla işlem yaparken, toplama ve çıkarma işlemi ancak kök içindeki ifadeler (yani dereceler ve içindeki sayı) aynı olduğunda yapılabilir.

Bunu, cebirsel ifadelerde benzer terimleri birleştirme kuralına benzetebiliriz.

Köklü Sayılarda Toplama İşlemi

Temel Kural:

Eğer kök içleri aynıysa, katsayılar toplanır ve köklü kısım aynı kalır:

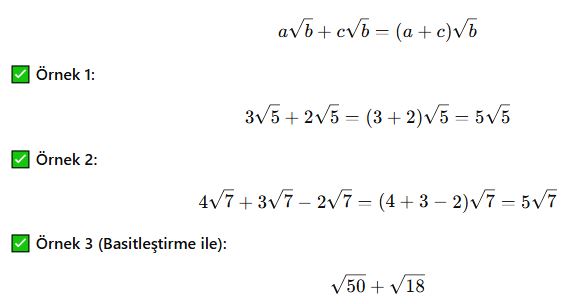
‼️ ÖNEMLİ:
Eğer kök içleri farklıysa, toplama işlemi yapılamaz.

❌ Yanlış Örnek:

Bu ifade sadeleşmez, çünkü kök içleri farklıdır.

Köklü Sayılarda Çıkarma İşlemi

Köklü sayılarda çıkarma işlemi de toplama gibi çalışır:

• Kök içleri aynıysa, katsayılar çıkarılır.

Genel Formül:

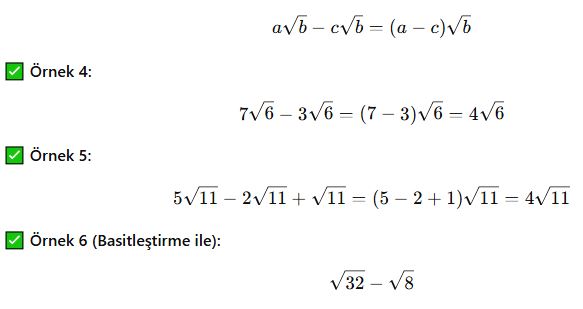
Farklı Kök Dereceleri İçeren Toplama ve Çıkarma İşlemleri

Eğer kök dereceleri farklıysa, işlemi yapmadan önce kök derecelerini eşitlemek gerekir.

Örnek 7:

Köklü Sayıları Toplama ve Çıkarma ile İlgili Karışık Sorular

Özet:

✅ Kök içleri aynı olan ifadeler toplanıp çıkarılabilir.
✅ Kök içleri farklı olan ifadeler doğrudan toplanamaz, önce sadeleştirilmelidir.
✅ Farklı kök derecelerine sahip ifadeler, kök dereceleri eşitlenerek işleme alınabilir.
✅ İfadeleri sadeleştirmek, işlemleri kolaylaştırır.

Köklü Sayılarda Çarpma ve Bölme İşlemi

Köklü sayılarla çarpma ve bölme işlemleri üs kurallarına benzer şekilde yapılır. Köklü ifadelerle işlem yaparken kök içleri aynı olan ifadeleri çarpmak veya bölmek daha kolaydır, ancak kök dereceleri farklı olduğunda öncelikle eşitlemek gerekir.

Köklü Sayılarda Çarpma İşlemi

Genel Kural:

​

Yani, aynı dereceden köklü ifadeler çarpıldığında, içlerindeki sayılar çarpılır ve aynı kök derecesinde yazılır.

Köklü Sayılarda Bölme İşlemi

Genel Kural:

​​

Aynı kök derecesindeki ifadeler bölünebilir ve kök içindeki sayılar bölünüp tekrar aynı köke yazılabilir.

Kök Dereceleri Farklı Olan İfadelerde Çarpma ve Bölme

Eğer kök dereceleri farklıysa, işlem yapmadan önce kök derecelerini eşitlemek gerekir.

Karmaşık Köklü İşlemler ve Sonuçları

Bazı işlemler kök derecesini sadeleştirme veya köklü ifadeyi üslü gösterime çevirme gerektirebilir.

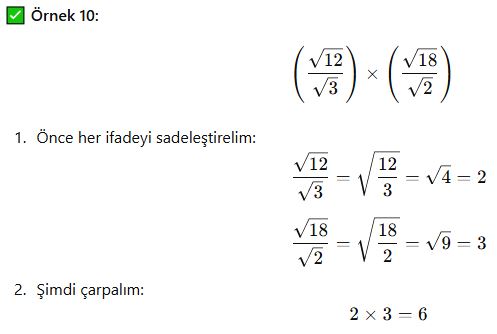
Özet:

✅ Çarpma işlemi için:

​

✅ Bölme işlemi için:

​​

✅ Kök dereceleri farklıysa, önce kök derecelerini eşitlemeliyiz.
✅ Sonrasında normal çarpma veya bölme işlemi yapılır.

Bazı Sayıların Kök Değerleri

Köklü ifadelerle işlem yaparken bazı sayıların karekök, küpkök ve daha yüksek dereceli kök değerlerini bilmek büyük bir avantaj sağlar. Özellikle TYT gibi sınavlarda zaman kazanmak için bazı temel kök değerleri ezberlemek gereklidir.

Kareköklü Sayıların Değerleri

Kareköklü sayılar en sık kullanılan köklü sayılardır. Tam kare olan sayıların karekökleri tam sayı çıkar.

Önemli Tam Kare Sayılar ve Kareköklü Değerleri

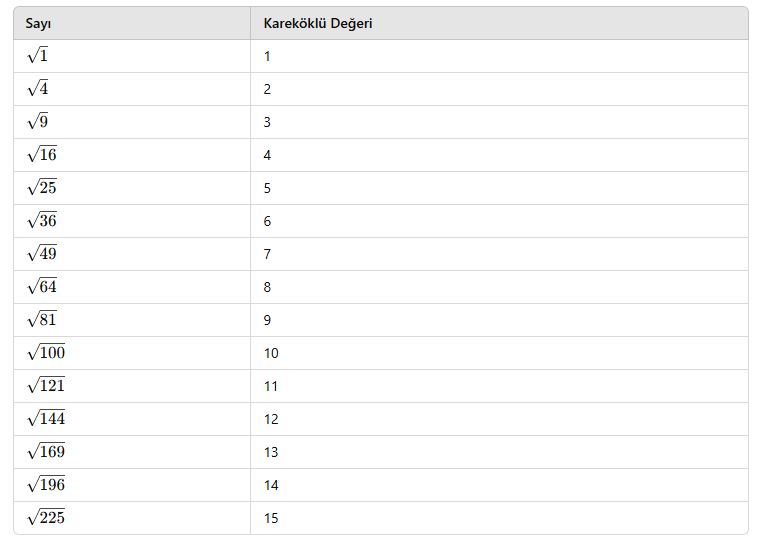
Bu değerler sınavlarda hızlı işlem yapmayı sağlar.

Kareköklü Tam Kare Olmayan Sayıların Yaklaşık Değerleri

Tam kare olmayan bazı sayıların köklerini yaklaşık olarak bilmek faydalıdır.

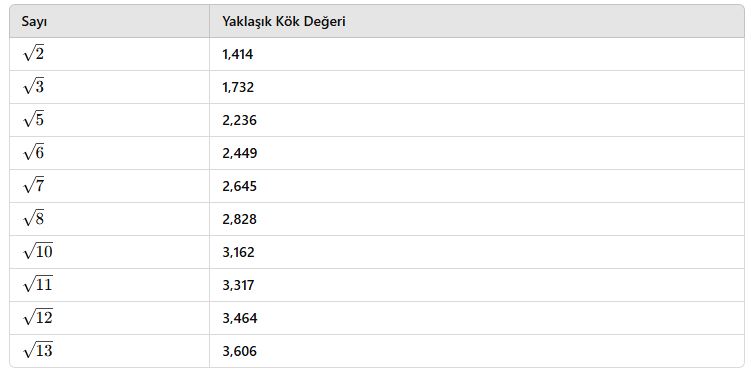
Bu değerleri yaklaşık olarak ezberlemek, sayı sıralama ve köklü işlemler yaparken büyük bir avantaj sağlar.

✅ Örnek:

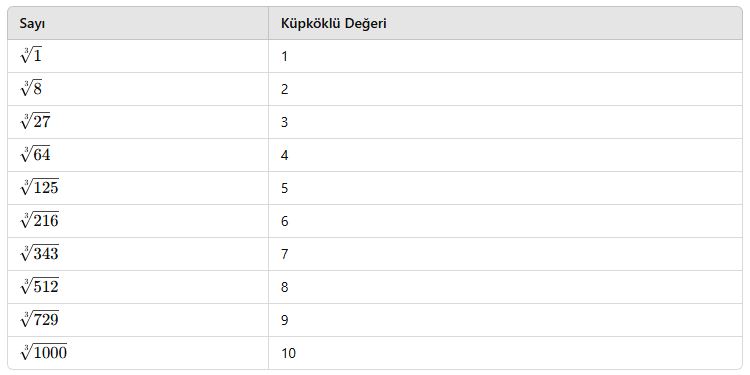
Küpköklü Sayıların Değerleri

Küpkök almak, bir sayının kendisiyle üç kez çarpılmasını tersine çevirir.

Önemli Tam Küp Sayılar ve Küpkökleri

Dördüncü Dereceden Kök Değerleri

Dördüncü dereceden kök almak, bir sayının kendisiyle dört kez çarpılmasını tersine çevirir.

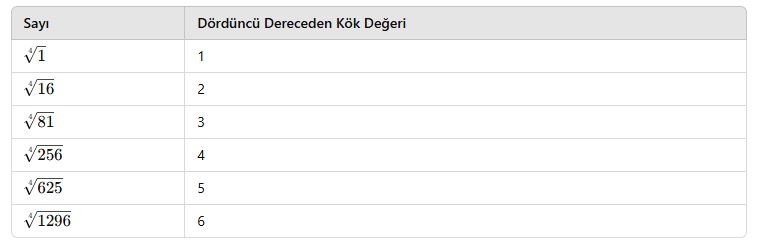
Bu kökler geometri ve fizik problemlerinde sıkça karşımıza çıkar.

Beşinci ve Daha Büyük Dereceli Kökler

Beşinci, altıncı ve daha büyük kökler nadiren kullanılır, ancak bazı özel durumlarda bilinmesi gerekir.

Kök Değerlerini Bilmenin Faydaları

🔹 Sayıları karşılaştırırken hızlı karar vermek için
🔹 Yaklaşık değerleri kullanarak işlemleri hızlandırmak için
🔹 Köklü sayılarla işlem yaparken hataları azaltmak için

✅ Örnek:

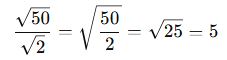
Bunu bilmek işlem hızınızı artırır.

Özet:

✅ Tam kare ve tam küp kökleri ezberlemek işlem hızınızı artırır.
✅ Tam kare olmayan köklerin yaklaşık değerlerini bilmek kıyaslama yapmayı kolaylaştırır.
✅ Dördüncü ve beşinci dereceden kökler özel durumlar için bilinmelidir.
✅ Bu bilgileri kullanarak köklü işlemleri daha hızlı çözebiliriz.

Köklü İfadelerin Tanım Aralığı

Bir köklü ifadenin tanımlı olması için kök içindeki sayının belirli şartları sağlaması gerekir.
Özellikle çift dereceli köklerde (kare kök, dördüncü kök vb.) tanım kümesini belirlemek önemlidir.

Çift Dereceli Köklü İfadelerin Tanım Şartları

Çift dereceli kökler, $n$ çift sayı olduğunda tanımlanır.
Bu durumda kök içindeki ifade negatif olmamalıdır.

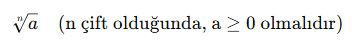
Önemli Kural:
Karekök içindeki sayı negatif olamaz!
Dördüncü, altıncı köklerde de aynı kural geçerlidir.

Eğer çift dereceli bir kökün içinde negatif bir sayı varsa, o ifade gerçek sayılar kümesinde tanımlı değildir ve yalnızca karmaşık sayılar kümesinde tanımlanabilir.

Ancak TYT Matematik kapsamında karmaşık sayılar işlenmez, bu yüzden negatif sayıların çift dereceli kökleri “tanımsız” kabul edilir.

Tek Dereceli Köklü İfadelerin Tanım Şartları

Tek dereceli köklerde (küp kök, beşinci kök vb.), kök içindeki sayı negatif olabilir.
Çünkü tek sayıda çarpım işlemi sonucu negatif olabilir.

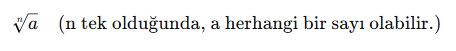
Sonuç olarak, tek dereceli kökler her zaman tanımlıdır, çift dereceli kökler ise sadece sıfır veya pozitif sayılar için tanımlıdır.

Değişken İçeren Köklü İfadelerin Tanım Aralığı

Eğer köklü ifadede bir değişken (x) varsa, tanımlı olduğu aralığı belirlemek için kök içinin sıfır veya pozitif olması gerektiğini kontrol ederiz.

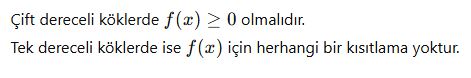
Kök Derecesine Göre Tanımlı Aralıkları Karşılaştırma

Özet:

✅ Çift dereceli köklü ifadelerde (√, ⁴√ vb.) kök içi negatif olamaz.
✅ Tek dereceli köklü ifadeler (³√, ⁵√ vb.) her zaman tanımlıdır.
✅ Değişkenli ifadelerde tanım aralığını belirlemek için kök içinin sıfır veya pozitif olması gereklidir.
✅ Paydada köklü ifade varsa, paydanın sıfır olmamasına dikkat edilmelidir.

Tek ve Çift Dereceli Köklü İfadeler

Köklü ifadeler derecelerine göre tek dereceli ve çift dereceli olmak üzere ikiye ayrılır. Bu ayrım, köklü ifadelerin tanımı, özellikleri ve işlem kuralları açısından büyük önem taşır.

Çift Dereceli Köklü İfadeler

Tanım:

• Çift dereceli köklü ifadeler n çift bir sayı olduğunda tanımlıdır.
• Kökün içindeki ifade negatif olamaz (gerçek sayılar kümesinde).

Özellikler:

✅ Kök içi negatif olamaz (gerçek sayılarda tanımsızdır).
✅ Kök içindeki pozitif sayılar her zaman pozitif bir sonuç verir.
✅ Çift dereceli köklerde mutlak değer alınarak sonuç elde edilir:

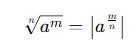
Tek Dereceli Köklü İfadeler

Tanım:

• Tek dereceli köklü ifadelerde kökün içindeki sayı her zaman tanımlıdır.
• Negatif bir sayı da kök içine alınabilir.

Özellikler:

✅ Pozitif sayılar pozitif olarak çıkar.
✅ Negatif sayılar negatif olarak çıkar.
✅ Tek dereceli kökler tüm real sayılar kümesinde tanımlıdır.

Çift ve Tek Dereceli Kökler Arasındaki Farklar

Bu farklar köklü ifadelerle işlem yaparken oldukça önemlidir.

Çift ve Tek Dereceli Köklerle İşlemler

Örnek 1: Kök Derecelerine Göre Tanımlılık

Örnek 2: Tek ve Çift Dereceli Köklerin Karşılaştırılması

Tek ve Çift Dereceli Köklerle Toplama ve Çıkarma

🔹 Çift dereceli köklerde sadece pozitif sonuçlar alınabilir.
🔹 Tek dereceli köklerde negatif sonuçlar alınabilir ve işlemler yapılabilir.

Örnek 3: Tek Dereceli Köklerle İşlem

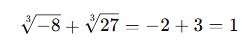
Örnek 4: Çift Dereceli Köklerle İşlem

Özet:

✅ Çift dereceli köklerde negatif sayılar tanımsızdır.
✅ Tek dereceli kökler negatif sayılar için tanımlıdır.
✅ Çift dereceli kökler her zaman pozitif sonuç verir.
✅ Tek dereceli köklerde sonuç işareti korunur.
✅ İşlemler sırasında kökün derecesine dikkat edilmelidir.

Köklü İfade İşlem Kuralları

Köklü ifadelerle işlem yaparken bazı temel kuralları bilmek, işlemleri hızlandırır ve hata yapma olasılığını azaltır.
Bu kurallar, çarpma, bölme, üslü ifadeye çevirme, kök derecelerini değiştirme ve sadeleştirme gibi işlemleri içerir.

Köklü İfadelerde Çarpma Kuralları

Genel Kural:
Aynı dereceden köklü ifadeler çarpılırken kök içindeki sayılar çarpılır ve tek bir kök içinde yazılır.

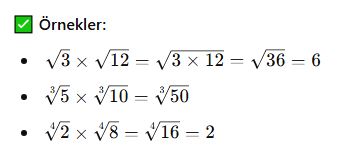
Önemli Not:
Kök dereceleri farklıysa, önce kök dereceleri eşitlenmelidir.

Köklü İfadelerde Bölme Kuralları

Genel Kural:
Aynı dereceden köklü ifadeler bölünürken kök içindeki sayılar bölünür ve tek bir kök içinde yazılır.

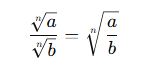
Köklü İfadelerde Üslü Gösterim Kuralları

Genel Kural:
Köklü ifadeler üslü ifade olarak şu şekilde yazılabilir:

Köklü ifadeleri üslü ifadeye dönüştürmek çarpma ve bölme işlemlerini daha kolay hale getirir.

🔹 Üstü olan köklü ifadeler:

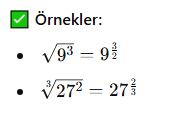
Kök Derecesini Genişletme ve Sadeleştirme Kuralları

Genel Kural:
Kök derecesi büyütülüp küçültülebilir.

🔹 Kök Derecesini Sadeleştirme:

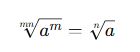
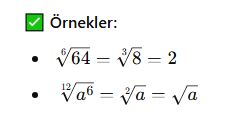
Köklü İfadelerde Kök İçine ve Dışına Alma Kuralları

🔹 Kök İçine Alma:
Bir katsayıyı kök içine alırken, kök derecesine göre üssü artırarak kök içine alırız.

🔹 Kök Dışına Alma:
Bir sayıyı kök dışına çıkarırken tam kare, tam küp vb. çarpanlara ayırarak kökten çıkarırız.

Köklü İfadelerde İşlem Önceliği Kuralları

Matematikte işlem önceliği kuralları köklü ifadeler için de geçerlidir.

1️⃣ Parantez içindeki işlemler yapılır.
2️⃣ Köklü ifadeler ve üslü işlemler yapılır.
3️⃣ Çarpma ve bölme işlemleri yapılır.
4️⃣ Son olarak toplama ve çıkarma yapılır.

✅ Örnek:

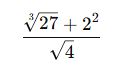
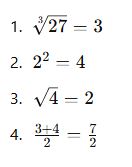
Karmaşık Köklü İşlemler ve Kurallar

Köklü ifadeler bazen birden fazla işlemi aynı anda içerebilir.

✅ Örnek 1:

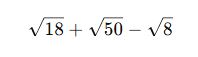
Köklü ifadeleri sadeleştirelim:

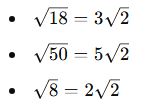
Şimdi işlemi yapalım:

✅ Örnek 2:

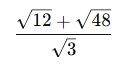
Önce sadeleştirme yapalım:

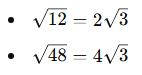
Toplayalım:

Bölme işlemini yapalım:

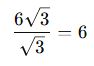
Özet:

✅ Köklü ifadeler çarpılırken veya bölünürken kök içleri işlem görür.
✅ Köklü ifadeler üslü ifadeye çevrilebilir.
✅ Kök içine ve dışına alma işlemleri dikkatli yapılmalıdır.
✅ İşlem önceliği kurallarına dikkat edilmelidir.

Benzer Terimlerle Köklü Sayılarda Toplama ve Çıkarma

Köklü sayılarla toplama ve çıkarma işlemi yapılırken yalnızca benzer köklü ifadeler birleştirilebilir.

✅ Benzer köklü ifadeler:

• Aynı dereceden köke sahiptirler.
• Kök içindeki ifadeler aynıdır.
• Katsayıları toplama ve çıkarma işlemine dahil edilir.

❌ Farklı köklü ifadeler:

• Farklı kök derecelerine veya farklı kök içlerine sahiptirler.
• Birbirleriyle doğrudan toplanamaz veya çıkarılamazlar.

Benzer Köklü Terimleri Tanıma

Genel Formül:

Farklı Kök İçeren Terimleri Benzer Hale Getirme

Eğer kök içleri farklıysa, bazen ifadeleri sadeleştirerek benzer hale getirebiliriz.

Farklı Kök Derecelerini Eşitleyerek İşlem Yapma

Eğer kök dereceleri farklıysa, işlem yapmadan önce kök derecelerini eşitlemek gerekir.

Karmaşık Toplama ve Çıkarma Soruları

✅ Örnek 4:

Benzer Terimlerle İşlemler İçin Kısa Kurallar

✅ Kök içleri aynı olan ifadeler direkt toplanır veya çıkarılır.
✅ Farklı kök içlerine sahip ifadeler sadeleştirilerek aynı hale getirilebilir.
✅ Farklı kök derecelerine sahip ifadeler ortak kök derecesine çevrilerek işleme alınabilir.
✅ İşlem önceliği kurallarına dikkat edilmelidir.

Köklü İfadelerin Üslü Gösterimi

Köklü ifadeleri üslü ifadelerle yazmak, işlem yapmayı kolaylaştırır ve özellikle çarpma, bölme, üslü işlemler gibi konularda avantaj sağlar.

Genel Kural:

Bir köklü ifade üslü biçimde şu şekilde yazılır:

Bu kural, her türlü köklü ifadeye uygulanabilir.

Küpköklü İfadelerin Üslü Gösterimi

Küpkök (n=3) için üslü gösterim:

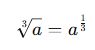
Dördüncü ve Daha Yüksek Dereceli Köklü İfadelerin Üslü Gösterimi

Genel Formül:

Üslü Sayıların Köklü Gösterimi

Eğer köklü bir ifade zaten üslü bir sayı içeriyorsa, şu kuralları kullanırız:

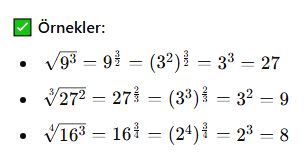
Üslü Gösterimde İşlem Kuralları

Köklü ifadeler üslü hale getirildikten sonra, üslü sayı kurallarıyla işlem yapılabilir.

Örnekler

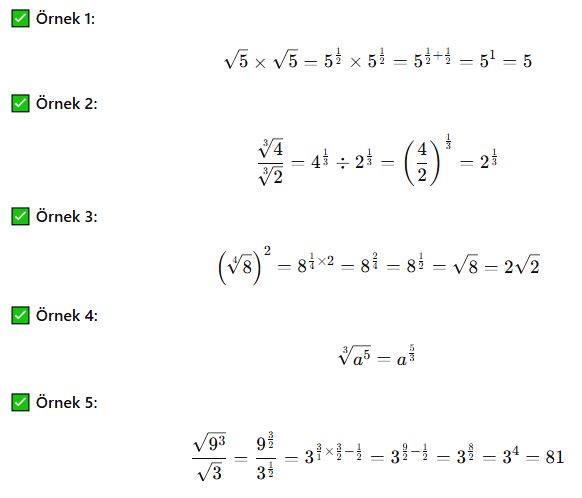
Üslü Gösterimde Pratik Bilgiler

🔹 Üslü ifadeleri kullanarak köklü işlemleri hızlandırabilirsiniz.
🔹 Bütün köklü ifadeler üslü biçimde ifade edilebilir.
🔹 İşlem önceliğine dikkat edilmelidir.

Özet:

✅ Köklü ifadeler üslü biçimde yazılabilir:

​

✅ Üslü ifadelerle çarpma, bölme ve üst alma işlemleri yapılabilir.
✅ Üslü gösterim sayesinde bazı işlemler daha kolay hale gelir.

Dereceleri Eşit İfadeler Arasında Çarpma

Köklü ifadelerle çarpma işlemi yaparken kök dereceleri eşitse, kök içindeki sayılar doğrudan çarpılarak tek bir kök içinde yazılabilir.

Genel Kural:

Aynı dereceli köklü ifadeler çarpılırken kök içindeki sayılar çarpılır ve sonuç aynı kök derecesi içinde kalır.

​

Bu kural, karekök (√), küpkök (∛) veya daha yüksek dereceli kökler için geçerlidir.

Kareköklerde Çarpma İşlemi (n=2)

​

✅ Örnekler:

​

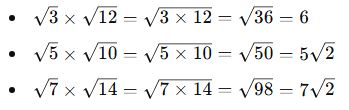
💡 Önemli Not: Sonuç tam kare değilse, kök dışına çıkabilen çarpanları ayırmak gerekir.

Küpköklü İfadelerde Çarpma (n=3)

​

✅ Örnekler:

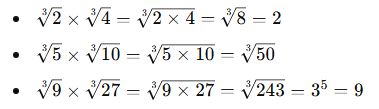
💡 Önemli Not: Küpköklerde tam küp olan sayılar kök dışına çıkarılabilir.

Daha Yüksek Dereceli Köklerde Çarpma (n=4,5,6 vb.)

​

✅ Örnekler:

​

💡 Önemli Not: Kök derecesi büyüdükçe tam çarpanları belirlemek işlemi kolaylaştırır.

Dereceleri Eşit Olan Üslü Sayılarla Çarpma

Eğer köklü ifadeler üslü biçimde yazılırsa, çarpma işlemi daha kolay hale gelir.

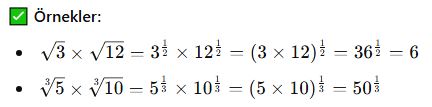
💡 Üslü ifadeye çevirerek işlem yapmak, karmaşık çarpma işlemlerinde büyük kolaylık sağlar.

Çarpma İşleminde Kök Derecelerini Eşitleme

Eğer kök dereceleri farklıysa, işlemi yapabilmek için önce ortak bir kök derecesine çevirmek gerekir.

Genel Kural:

✅ Örnek:

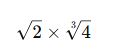
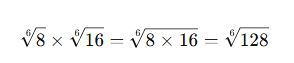
Karmaşık Çarpma İşlemleri

Bazı sorularda önce köklü ifadeler sadeleştirilmeli, ardından çarpma yapılmalıdır.

✅ Örnek:

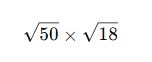
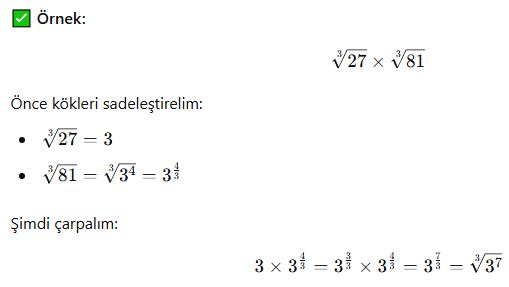
Özet:

✅ Aynı dereceli kökler çarpılırken, kök içindeki sayılar çarpılıp tek bir kök içinde yazılır.
✅ Tam kare ve tam küp olan sayılar kök dışına çıkarılmalıdır.
✅ Farklı kök dereceleri varsa, önce ortak bir kök derecesine çevrilmelidir.
✅ Üslü gösterime çevirerek işlem yapmak çarpma işlemlerini kolaylaştırabilir.

Dereceleri Eşit İfadeler Arasında Bölme

Köklü ifadelerde bölme işlemi kök dereceleri eşitse oldukça kolaydır. Kök içindeki ifadeler doğrudan bölünerek tek bir kök içinde yazılır.

Genel Kural:

Eğer iki köklü ifade aynı kök derecesine sahipse, şu formül kullanılır:

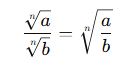
Bu kural, karekök (√), küpkök (∛) veya daha yüksek dereceli kökler için geçerlidir.

💡 Önemli Not:
Eğer kök dereceleri farklıysa, önce kök derecelerini eşitlemek gerekir.

Kareköklerde Bölme İşlemi (n=2)

Karekök ifadelerinde bölme işlemi şu şekilde yapılır:

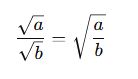
💡 Eğer paydanın kök içindeki değeri tam kare değilse, rasyonel hale getirme işlemi yapılabilir.

Küpköklü İfadelerde Bölme (n=3)

Küpkök ifadelerinde bölme işlemi şu şekildedir:

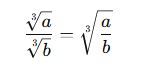
💡 Önemli Not:
Sonucu sadeleştirmek için tam küpleri belirlemek faydalıdır.

Daha Yüksek Dereceli Köklerde Bölme (n=4,5,6 vb.)

Genel bölme formülü şu şekildedir:

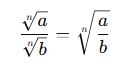
Köklü İfadelerde Payda Rasyonelleştirme

Eğer paydada köklü bir ifade varsa, bu ifadeyi rasyonel hale getirmek gerekir.

✅ Örnek:

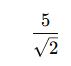
Farklı Kök Dereceleri Arasında Bölme İşlemi

Eğer kök dereceleri farklıysa, önce ortak bir kök derecesine getirilmelidir.

Genel formül:

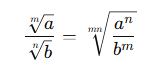
✅ Örnek:

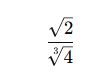
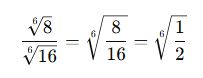
Karmaşık Bölme İşlemleri

Bazı bölme işlemleri önce sadeleştirilip sonra yapılmalıdır.

✅ Örnek:

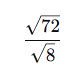
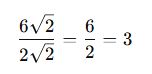
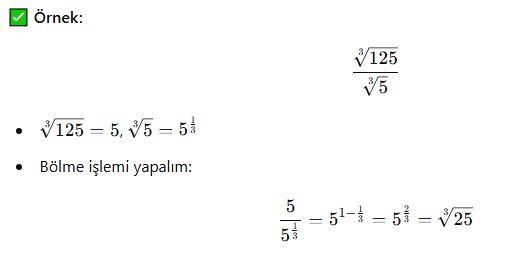
Özet:

✅ Aynı kök derecesine sahip ifadeler, kök içi bölünerek yazılabilir.
✅ Paydada köklü ifade varsa, rasyonel hale getirilmelidir.
✅ Farklı kök dereceleri varsa, önce ortak bir kök derecesine çevrilmelidir.
✅ Köklü ifadeleri üslü hale getirerek bölme işlemleri kolaylaştırılabilir.

Derece İşlemleri ve Kök Dışına Çıkarma

Köklü ifadelerde derece işlemleri ve kök dışına çıkarma işlemleri, köklü ifadelerle daha kolay işlem yapabilmek için oldukça önemlidir. Bu kurallar sayesinde köklü ifadeleri sadeleştirebilir, işlemleri hızlandırabiliriz.

Kök Derecesini Değiştirme Kuralları

Bazen köklü ifadeleri işleme uygun hale getirmek için kök derecesini genişletmek veya sadeleştirmek gerekir.

Genel Kural:

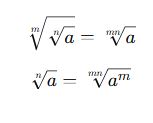
💡 Önemli Not: Eğer işlemlerde kök derecelerini eşitlemek gerekiyorsa, küçük kök derecesini genişletmek faydalıdır.

Kök Dışına Çıkarma Kuralları

Bir köklü ifadeyi daha sade hale getirmek için kök dışına çıkarma işlemi kullanılır.
Bu işlem, kök içindeki tam kare (veya tam küp vb.) sayıları ayırarak yapılır.

Genel Kural:

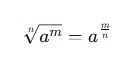
Kök İçine Alma Kuralları

Bazen işlemi kolaylaştırmak için sayıları tekrar kök içine almak gerekebilir.

Genel Kural:

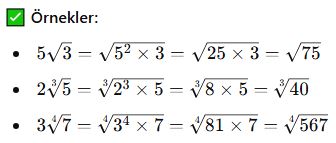
💡 Önemli Not: Kök içindeki sayıları tam kare veya tam küp yaparak tekrar kök içine almak mümkündür.

Kök Derecelerini Eşitleme İşlemi

Farklı kök derecelerine sahip ifadeleri aynı kök derecesine çevirmek için şu formül kullanılır:

Bazen iki farklı kök derecesini ortak bir kök derecesinde birleştirmek gerekir.

✅ Örnek:

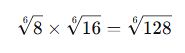
Kök Dışına Çıkarma İçin Özel Sayılar

Bazı köklü sayılar, kök dışına daha kolay çıkarılabilen tam kare, tam küp vb. sayılar içerir.

Bu sayılar, kök dışına direkt çıkabildiği için işlemleri hızlandırır.

✅ Örnek:

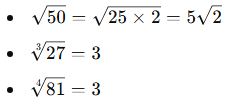
💡 Önemli Not: Eğer kök içinde tam kare veya tam küp olmayan sayılar varsa, mümkün olduğunca sadeleştirilmelidir.

Karmaşık Kök Dışına Çıkarma ve İşlem Soruları

✅ Örnek 1:

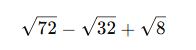
✅ Örnek 2:

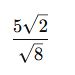
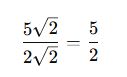
Özet:

✅ Kök dereceleri genişletilebilir ve sadeleştirilebilir.
✅ Kök içindeki tam kare veya tam küp çarpanlar kök dışına çıkarılabilir.
✅ Bazen sayıları kök içine almak işlem yapmayı kolaylaştırabilir.
✅ Farklı dereceli kökler, ortak bir kök derecesine çevrilerek işleme alınabilir.
✅ Özel tam kare, tam küp sayılar kök dışına daha kolay çıkarılabilir.

İç İçe Köklü İfadeler

İç içe köklü ifadeler, bir köklü ifadenin içinde başka bir köklü ifadenin bulunmasıyla oluşan matematiksel ifadelerdir.
Bu tür ifadeleri sadeleştirmek ve işlem yapmak için belirli kurallar kullanılır.

İç İçe Köklerin Genel Formülü

Eğer bir köklü ifade başka bir kök içinde yer alıyorsa, şu dönüşüm formülü kullanılır:

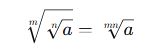
Bu formül, iç içe kökleri tek bir kök haline getirmek için kullanılır.

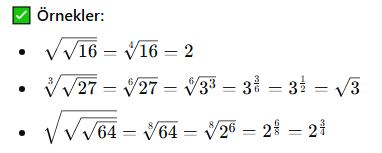
💡 Önemli Not: Eğer iç içe köklerin dereceleri farklıysa, önce ortak bir kök derecesine çevirmek gerekir.

İç İçe Kökleri Açma Kuralları

Bazen iç içe köklü ifadeler rasyonel bir şekilde açılabilir.

Eğer ifade şu formdaysa:

Bu, aşağıdaki gibi iki köklü terimin çarpımı olarak yazılabilir:

Bu tür ifadeleri çözmek için şu yöntemi kullanırız:

Bu açılımı kullanarak x ve y değerlerini bulabiliriz.

✅ Örnek 1:

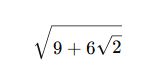
Sonuç:

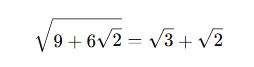
İç İçe Kökleri Tek Kök Haline Getirme

Bazı iç içe köklü ifadeler, tek bir kök olarak ifade edilebilir.

✅ Örnek 3:

İç İçe Köklerin Çarpımı ve Bölümü

Eğer iki iç içe köklü ifade çarpılıyorsa veya bölünüyorsa, önce sadeleştirme yapmak faydalıdır.

✅ Örnek 4: Çarpma İşlemi

İç İçe Köklerin Rasyonelleştirilmesi

Paydada iç içe köklü ifade varsa, çift eşlenik kullanılarak rasyonel hale getirilebilir.

✅ Örnek 5: Bölme İşlemi

Özet:

✅ İç içe köklü ifadeler tek bir kök haline getirilebilir.
✅ Bazı iç içe köklü ifadeler açılarak sadeleştirilebilir.
✅ Çarpma ve bölme işlemlerinde eşlenik kullanılabilir.
✅ İşlem yaparken özdeşliklerden yararlanılmalıdır.

Köklü Denklemler

Köklü denklemler, bir veya birden fazla köklü ifadenin yer aldığı denklemlerdir.
Bu tür denklemleri çözmek için bazı temel kurallar ve yöntemler kullanılır.

Köklü Denklemleri Çözme Adımları

Bir köklü denklemi çözerken aşağıdaki adımları takip etmeliyiz:

1️⃣ Köklü ifadeyi yalnız bırak
2️⃣ Her iki tarafın karesini (veya küpünü) al
3️⃣ Eğer köklü ifade hâlâ varsa, işlemi tekrar et
4️⃣ Denklemi çöz ve kökleri doğrula

💡 Önemli Not:
Köklü denklemler yanlış kök (extraneous root) üretebilir. Bulduğun kökleri denkleme koyarak doğrulaman gerekir.

Basit Köklü Denklemler

Genel Formül:

Daha Karmaşık Köklü Denklemler

Bir Tarafı Köklü, Diğer Tarafı Sabit Sayı Olan Denklemler

✅ Örnek 2:

Köklü İfade İçeren Denklemler

✅ Örnek 3:

💡 Yanlış kökleri bulmamak için her zaman doğrulama yap!

Birden Fazla Köklü Terim İçeren Denklemler

✅ Örnek 4:

Doğrulama:
Bu çözümü yerine koyup doğrulamak gerekir.

İç İçe Köklü Denklemler

✅ Örnek 5:

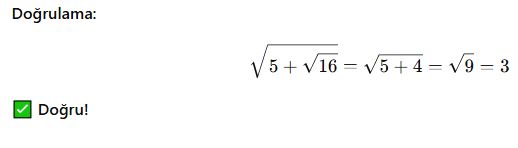
Köklü Denklem Çözmenin Püf Noktaları

🔹 Köklü ifadeyi yalnız bırak
🔹 Her iki tarafın karesini alırken dikkatli ol
🔹 Yanlış kökleri önlemek için sonucu denkleme koyarak doğrula
🔹 İç içe köklü ifadelerde iki kez kare alma işlemi gerekebilir

Özet:

✅ Basit köklü denklemleri çözmek için her iki tarafın karesi alınır.
✅ Birden fazla köklü terim varsa, köklerden biri yalnız bırakılıp sırasıyla karesi alınır.
✅ İç içe köklü ifadelerde iki kez kare almak gerekebilir.
✅ Yanlış kökleri (extraneous root) kontrol etmek için çözümü yerine koyarak doğrulamak şarttır.

Köklü Eşitsizlikler

Köklü ifadeler içeren eşitsizlikleri çözerken, kök içinin tanımlı olması, kare alma işlemleri ve işaret değişiklikleri gibi noktalara dikkat etmek gerekir.

Köklü Eşitsizlikleri Çözme Adımları

1️⃣ Kök içinin tanım aralığını belirle (çift dereceli köklerde kök içi negatif olamaz).
2️⃣ Eşitsizliği çözerken her iki tarafın karesini al (işaret değişikliği olup olmadığını kontrol et).
3️⃣ Kare alma işleminden sonra elde edilen eşitsizliği çöz.
4️⃣ Bulunan kökleri başlangıçtaki tanım kümesiyle karşılaştır ve uygun çözümü belirle.

Basit Köklü Eşitsizlikler

Genel Formül:

Karmaşık Köklü Eşitsizlikler

Eğer köklü ifade bir terim içeriyorsa, öncelikle kökü yalnız bırak.

✅ Örnek 2:

Negatif Sayılarla Köklü Eşitsizlikler

Çift dereceli kökler daima 0 veya pozitif olduğu için, negatif sayılarla yapılan eşitsizlikler çözüm vermez.

✅ Örnek 3:

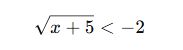
Köklü bir ifade negatif olamayacağı için bu eşitsizliğin çözümü yoktur.
Sonuç: Çözüm Kümesi: ∅

İki Tarafında Köklü İfade Olan Eşitsizlikler

Eğer iki tarafta da köklü ifadeler varsa, her iki tarafın karesi alınarak çözüm yapılır.

✅ Örnek 4:

Ayrıca kök içlerinin tanımlı olması için:

Şimdi tüm aralıkları birleştirelim:

Sonuç:

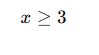
İç İçe Köklü Eşitsizlikler

✅ Örnek 5:

Mutlak Değer ve Köklü Eşitsizlikler

Bazen köklü ifadeler mutlak değer eşitsizliklerine dönüşebilir.

✅ Örnek 6:

Özet:

✅ Köklü ifadeleri içeren eşitsizliklerde önce kökü yalnız bırakmalıyız.
✅ Her iki tarafın karesi alınırken, kökün derecesine ve işaret değişikliğine dikkat edilmelidir.
✅ Yanlış çözümleri önlemek için tanım kümeleri belirlenmelidir.
✅ Mutlak değer ve iç içe köklü ifadelerle karşılaşıldığında, mutlak değer kuralları uygulanmalıdır.

Köklü Sayılarla Problemler

Köklü sayılarla ilgili problemler geometri, hız-zaman, oran-orantı ve günlük yaşam problemleri gibi farklı konuları içerebilir.
Bu problemleri çözerken kök alma, sadeleştirme ve rasyonelleştirme kurallarına dikkat etmek gerekir.

Temel Problem Türleri

📌 Uzunluk, Alan ve Hacim Problemleri
📌 Hız-Zaman Problemleri
📌 Oran-Orantı Problemleri
📌 Geometrik Problemler
📌 Köklü Sayılar İçeren Denklem Problemleri

Uzunluk ve Alan Problemleri

✅ Örnek 1: Bir Karede Kenar Uzunluğu

Bir karenin alanı 50 cm² ise, kenar uzunluğu kaç cm’dir?

🔹 Çözüm:
Karenin alanı şu formülle bulunur:

✅ Örnek 2: Dikdörtgenin Köklü Uzunluğu

Hız-Zaman Problemleri

✅ Örnek 3: Köklü Hız Problemi

✅ Örnek 4: İki Araç Arasındaki Mesafe

Oran-Orantı Problemleri

✅ Örnek 5: Bir Karışım Problemi

✅ Örnek 6: Köklü Oran Problemi

Geometrik Problemler

✅ Örnek 7: Üçgenin Hipotenüsü

Köklü Sayılar İçeren Denklem Problemleri

✅ Örnek 8: Denklemin Çözümü

Bir sayı kendisinin karekökü ile çarpıldığında 72 oluyor. Bu sayı nedir?

Özet:

✅ Köklü sayılar günlük yaşam, geometri ve fizik problemlerinde kullanılır.
✅ Köklü uzunluklar, alanlar ve hacimler hesaplanırken sadeleştirme işlemi yapılmalıdır.
✅ Hız-zaman ve oran-orantı problemlerinde köklü işlemler düzenli yapılmalıdır.
✅ Denklem içeren problemler çözüldükten sonra kök doğrulaması yapılmalıdır.

Köklü Sayılarla Denklem Sistemleri

Köklü sayılar içeren denklem sistemlerini çözerken denklem sadeleştirme, her iki tarafın karesini alma ve yerine koyma yöntemleri kullanılır.

Bu tür sistemler genellikle iki bilinmeyenli denklem sistemleri olarak karşımıza çıkar.

Temel Denklem Çözme Yöntemleri

📌 Yerine Koyma Yöntemi (Substitution Method)
📌 Eliminasyon (Denklem Eşitleme) Yöntemi
📌 Her İki Tarafın Karesini Alma Yöntemi

Bu yöntemler, köklü ifadeleri içeren doğrusal ve doğrusal olmayan denklem sistemlerinde kullanılır.

Köklü Sayılarla Denklem Sistemleri Çözme Yöntemleri

Yerine Koyma Yöntemiyle Çözüm

✅ Örnek 1:

Tekrar karesini alarak çözebiliriz, ancak denklemin karmaşık hale gelmemesi için burada uygun $y$ değerlerini deneyerek çözüm bulabiliriz.

Çözüm: (x, y) = (4, 3)

Eliminasyon Yöntemiyle Çözüm

✅ Örnek 2:

Her İki Tarafın Karesini Alma Yöntemi

Bu yöntem, bir köklü ifade içeren denklem sistemlerinde kullanılır.

✅ Örnek 3:

Şimdi X yerine koyma yaparak ikinci denklemle çözebiliriz.

Bu tür denklemler genellikle deneme yanılma veya köklü ifadeleri azaltma yöntemi ile çözülebilir.

Çözüm: (x, y) = (1, 4)

Karmaşık Denklem Sistemleri

Bazen köklü denklemler üstel veya çarpanlara ayrılabilen ifadeler içerir.

✅ Örnek 4:

Denklem Sistemlerinde Özel Durumlar

1️⃣ Eşlenik Kullanarak Çözüm:

Bazı köklü sistemlerde eşlenik kullanılarak çözüm yapılır.

✅ Örnek 5:

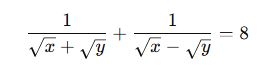
Eşlenik çarpma yöntemi kullanarak işlemi çözebiliriz.

Özet:

✅ Köklü denklemler genellikle yerine koyma, eliminasyon veya karesini alma yöntemi ile çözülür.
✅ İki köklü ifade içeren denklemlerde köklerden biri yalnız bırakılarak çözüm yapılır.
✅ Denklemler toplama-çıkarma yöntemiyle sadeleştirilerek çözülebilir.
✅ Yanlış çözümleri önlemek için bulunan kökler yerine konularak doğrulama yapılmalıdır.

Köklü Sayılarla Denklem Problemleri

Köklü sayılar içeren denklemler geometri, oran-orantı, hız-zaman, sayı ve yaş problemleri gibi farklı konularda karşımıza çıkar.
Bu tür problemlerde kök alma, sadeleştirme, her iki tarafın karesini alma ve yerine koyma yöntemleri kullanılır.

Köklü Sayılar İçeren Sayı Problemleri

✅ Örnek 1: Bir Sayının Kare Kökü ile İlgili Problem

Bir sayının karekökü, kendisinin 3 fazlasına eşittir.
Bu sayı kaçtır?

✅ Örnek 2: Sayının Karekökü ile Çarpımı

Bir sayının kendisi ile karekökünün çarpımı 72 ise, bu sayı kaçtır?

Köklü Sayılar İçeren Oran-Orantı Problemleri

✅ Örnek 3: Oran Problemi

Köklü Sayılar İçeren Hız-Zaman Problemleri

✅ Örnek 4: Hız Problemi

Köklü Sayılar İçeren Yaş Problemleri

✅ Örnek 5: Yaş Problemi

Ali’nin yaşı babasının yaşının kareköküne eşittir.
Babasının yaşı 49 yıl olduğuna göre, Ali’nin yaşı kaçtır?

🔹 Çözüm:
Ali’nin yaşı:

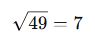
Sonuç:
Ali 7 yaşındadır.

Köklü Sayılar İçeren Geometri Problemleri

✅ Örnek 6: Dik Üçgende Hipotenüs

✅ Örnek 7: Alan Problemi

Köklü Sayılar İçeren Denklem Problemleri

✅ Örnek 8: Bir Sayının Ters Oranı

Bir sayı, karekökünün 2 katının 3 eksiğine eşittir.
Bu sayı kaçtır?

Sonuç:
Gerçek çözüm yoktur.

Özet:

✅ Köklü sayılar içeren problemler sayı, oran-orantı, hız-zaman, yaş ve geometri alanlarında karşımıza çıkar.
✅ Problemleri çözerken kök alma, sadeleştirme ve yerine koyma yöntemleri kullanılır.
✅ Elde edilen köklerin geçerli olup olmadığı doğrulama ile kontrol edilmelidir.

Köklü Sayılarda Üslü İşlemler

Köklü sayılarla üslü işlemler yapılırken kök ve üs ilişkisi kullanılır.
Özellikle köklü ifadeleri üslü ifadeye çevirerek işlemleri kolaylaştırabiliriz.

Köklü İfadelerin Üslü Gösterimi

Bir köklü ifade üslü biçimde şu şekilde yazılabilir:

Bu kural, köklü ifadelerle işlem yaparken üsleri daha kolay yönetmemizi sağlar.

✅ Örnekler:

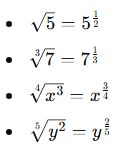
Köklü Sayılarla Üslü İşlemler Kuralları

Aşağıdaki üs kuralları, köklü ifadelerle işlem yaparken de geçerlidir:

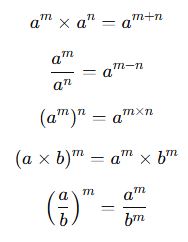
Köklü Sayılarla Çarpma ve Bölme İşlemleri

Çarpma İşlemi

Eğer kök dereceleri eşitse, kök içindeki sayılar çarpılıp tek bir kök içinde yazılabilir:

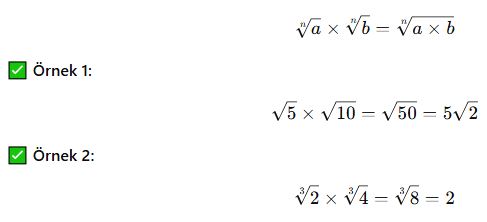
Bölme İşlemi

Eğer kök dereceleri eşitse, kök içindeki ifadeler bölünüp tek bir kök içinde yazılır:

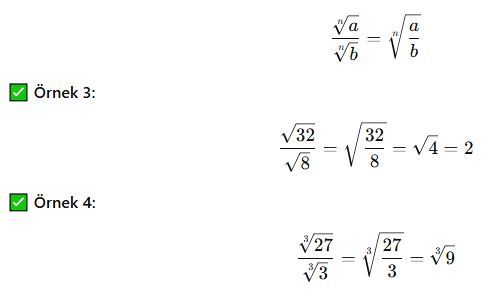
Köklü Sayılarda Üs Almak

Köklü bir sayının üssünü alırken şu kural kullanılır:

Bu kural sayesinde köklü sayılar tamamen üslü ifadeye dönüştürülerek işlem yapılabilir.

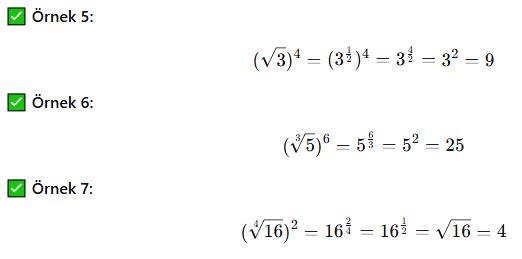
Negatif Üsler ve Köklü İfadeler

Bir köklü ifadede negatif üs varsa, bu ifade kesirli hale getirilebilir:

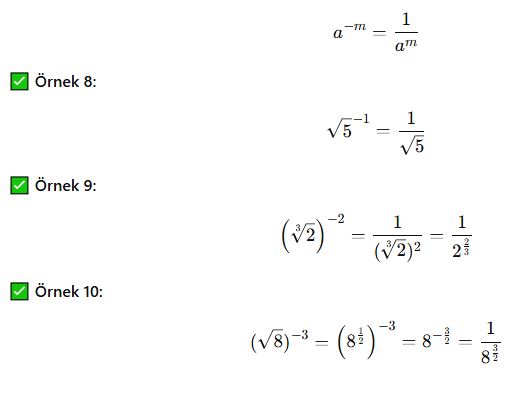
Köklü Üslü Sayılarda Karışık İşlemler

Bazen birden fazla kuralın bir arada kullanılması gerekir.

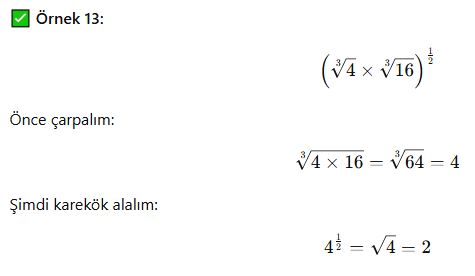
Özet:

✅ Köklü ifadeler üslü biçime çevrilebilir.
✅ Çarpma ve bölme işlemlerinde kök dereceleri eşitlenerek işlem yapılır.
✅ Üs alma işlemlerinde kök ve üs kuralları birlikte kullanılır.
✅ Negatif üsler ters çevirme kuralı ile sadeleştirilir.
✅ Karmaşık işlemler yapılırken önce kök sadeleştirilir, ardından üslü işlem uygulanır.

Köklü Sayılarla Eşlenik Kullanımı

Köklü ifadelerde eşlenik, özellikle rasyonel hale getirme (paydada kök bırakmama) ve çarpanlara ayırma işlemlerinde kullanılır.
Bu yöntem, özellikle kesirli ifadelerde paydanın kökten kurtarılmasını sağlar.

Eşlenik Nedir?

Eşlenik, köklü ifadelerde işaretleri ters çevrilerek oluşturulan bir ifadedir.
Eşlenik çarpıldığında kökten kurtulmamızı sağlar.

✅ Genel Formül:

Bu ifade çarpanlar arasındaki farklar çarpımıdır ve köklü ifadeyi ortadan kaldırır.

✅ Örnekler:

Payda Rasyonelleştirme (Köklü Paydalardan Kurtulma)

Eğer bir kesirin paydasında kök varsa, eşleniği ile çarparak rasyonel hale getirilebilir.

Tek Terimli Paydalar

Bu ifadeyi eşleniği ile çarparak paydadan kökü kaldırabiliriz.

✅ Örnek 1:

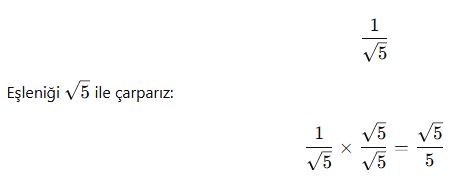
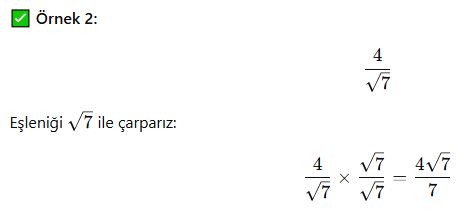
Çift Terimli Paydalar

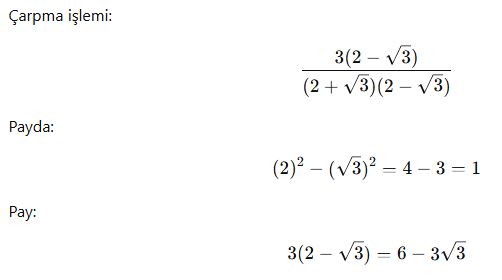
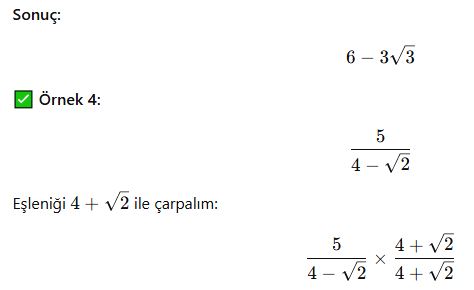
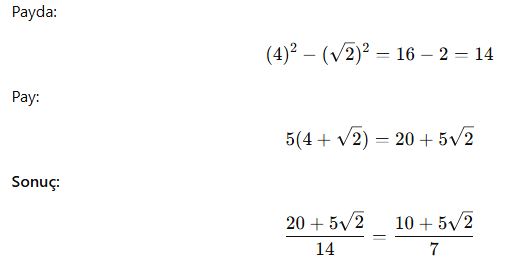
Eşlenik Kullanarak Köklü Denklem Çözme

✅ Örnek 5:

Eşlenik Kullanarak Toplama ve Çıkarma İşlemleri

✅ Örnek 6:

Özet:

✅ Eşlenik, paydadaki kökü yok etmek için kullanılır.
✅ Tek terimli köklü paydalar, aynı köklü sayı ile çarpılarak rasyonelleştirilir.
✅ İki terimli paydalar, eşleniği ile çarpılarak sadeleştirilir.
✅ Köklü denklemler eşlenik kullanılarak çözülebilir.
✅ Köklü sayılarla toplama ve çıkarma işlemlerinde eşlenik bazen işlemi sadeleştirmek için kullanılır.