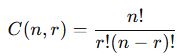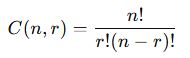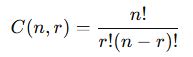TYT Matematik Permütasyon ve Kombinasyon Konu Anlatımı

Matematikte dizilimler ve seçimler, birçok gerçek dünya probleminde karşımıza çıkar. Günlük hayatımızda telefon numaralarımız, araba plakaları, şifre kombinasyonları ve takımların oluşturulması gibi pek çok durumda permütasyon ve kombinasyon kavramlarını kullanırız.

• Permütasyon: Bir grup nesnenin sıralı bir şekilde dizilmesini ifade eder.
• Kombinasyon: Bir grup nesnenin sıra gözetmeksizin seçilmesini ifade eder.

Bu ünitede, permütasyon ve kombinasyon kavramlarını detaylı bir şekilde ele alacağız. Öncelikle permütasyon konusuyla başlayalım. 🚀

Permütasyon

Permütasyon, bir kümedeki elemanların belirli bir sıraya göre dizilmesi anlamına gelir. Sıra önemli olduğu için farklı dizilişler farklı permütasyonlar olarak kabul edilir.

Örneğin, A, B, C harflerini farklı şekillerde dizelim:

• ABC
• ACB
• BAC
• BCA
• CAB
• CBA

Burada 3 farklı harfi farklı sıralarla dizerek 6 farklı permütasyon elde ettik.

Matematiksel olarak permütasyon,  şeklinde gösterilir ve şu formülle hesaplanır:

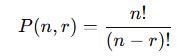
Permütasyon Tanımı

Permütasyon Nedir?

Permütasyon, bir kümede bulunan nesnelerin belirli bir diziliş veya sıralama ile düzenlenmesini ifade eder. Sıra önemlidir, yani aynı elemanların farklı sıralamalarına farklı permütasyonlar denir.

📌 Örnek:
A, B, C harflerini farklı şekillerde dizelim:

• ABC
• ACB
• BAC
• BCA
• CAB
• CBA

Burada 3 harfi 6 farklı sıralama ile düzenleyebildik.

Matematiksel olarak permütasyon şu formülle hesaplanır:

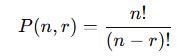
Burada:

• n → Toplam eleman sayısı
• r → Seçilecek ve sıralanacak eleman sayısı
• ! (faktöriyel) → Bir sayının kendisinden küçük bütün pozitif tam sayılarla çarpımıdır.

Örnek 1: Basit Permütasyon Hesaplama

Örnek:
5 farklı öğrenci arasından 3’ü seçilip sıralanacaktır. Kaç farklı diziliş mümkündür?

📌 Çözüm:

✅ Sonuç: 5 öğrenci arasından 3’ü seçilip sıralandığında 60 farklı diziliş mümkündür.

Permütasyonun Kullanım Alanları

Permütasyon, birçok farklı alanda kullanılmaktadır:

• Telefon numaraları ve şifreler: Şifre oluştururken belirli sayılar veya harfler belirli bir sırayla dizilir.
• Yarışmalar ve sıralamalar: Bir yarışmadaki sporcuların kaç farklı şekilde derece alabileceğini hesaplamak için kullanılır.
• Oturma düzenleri: Belirli kişileri belirli sandalyelere yerleştirirken kaç farklı oturma düzeni olacağını hesaplamak için kullanılır.

Bir Örnekle Permütasyon

Permütasyon, sıralamanın önemli olduğu durumlarda kullanılan bir yöntemdir. Bunu daha iyi anlamak için farklı senaryolardan örneklerle inceleyelim.

Örnek 1: Farklı Öğrencilerin Sıralanması

Bir sınıfta 4 öğrenci vardır: Ali, Burak, Ceren, Deniz.
Bu 4 öğrenci yan yana kaç farklı şekilde oturabilir?

📌 Çözüm:

✅ Sonuç: 4 öğrenci yan yana 24 farklı şekilde oturabilir.

Örnek 2: Podyuma Çıkış Sıralaması

Bir yarışmada 6 yarışmacı vardır. Yarışmacılar podyuma çıkarken ilk 3 sırada kimlerin olacağı ve sıralamanın nasıl olacağı önemlidir. Kaç farklı çıkış sırası olabilir?

📌 Çözüm:

✅ Sonuç: 6 yarışmacıdan 3’ü podyuma 120 farklı şekilde çıkabilir.

Örnek 3: Şifre Kombinasyonları

Bir bilgisayar şifresi 3 harften oluşmaktadır ve harfler A, B, C, D, E seçeneklerinden seçilmektedir. Her harf farklı olmak zorundadır.
Kaç farklı şifre oluşturulabilir?

📌 Çözüm:

✅ Sonuç: Bu şifreleme yöntemiyle 60 farklı şifre oluşturulabilir.

Özet

• Sıralamanın önemli olduğu durumlarda permütasyon kullanılır.
• Hesaplama için şu formül kullanılır:

​

• Önemli kullanım alanları:
  ✅ Öğrencilerin sıralanması
  ✅ Yarışmalardaki sıralamalar
  ✅ Şifreleme sistemleri
  ✅ Oyunlardaki kombinasyonlar

Çoklu Kümelerde (Tekrarlı) Permütasyon

Tekrarlı permütasyon, aynı nesnenin birden fazla kez seçildiği ve sıralandığı durumları ifade eder. Bu durumda, tekrarlanan nesnelerin sıralamaları da dikkate alınır, ancak benzer nesnelerin yer değişmesi farklı bir dizilim oluşturmaz.

1. Tekrarlı Permütasyon Nedir?

Bir kümede bazı elemanlar birbirinin aynı ise, bu elemanların sıralanması farklı olmasına rağmen sonuç aynı kabul edilir. Yani, aynı elemanlar tekrarlandığında permütasyonlar da tekrar edecektir.

Formül:
Eğer bir kümemizde toplam n eleman varsa ve bu elemanlardan bazıları tekrarlanıyorsa, tekrarlı permütasyon şu şekilde hesaplanır:

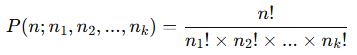
2. Örnek 1: Tekrarlı Permütasyon – Aynı Harflerle Şifre Oluşturma

Bir şifrede A, A, B, C, D harfleri kullanılacaktır. Bu harflerle kaç farklı şifre oluşturulabilir?

📌 Çözüm:

Formülü uygulayalım:

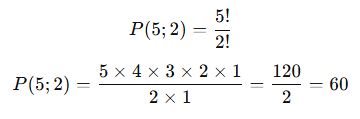
✅ Sonuç: A, A, B, C, D harfleriyle 60 farklı şifre oluşturulabilir.

3. Örnek 2: Tekrarlı Permütasyon – Aynı Nesnelerle Sıralama

Bir sınıfta 3 kız ve 2 erkek öğrenci vardır. Bu 5 öğrenci arasından 5 farklı şekilde sıralama yapılacak ancak kızlar aynı pozisyonlarda tekrarlayarak sıralanacak. Kaç farklı sıralama yapılabilir?

📌 Çözüm:

• Toplam öğrenci sayısı: n=5
• Kız öğrenciler 3 kez tekrar ediyor.

Formülü uygulayalım:

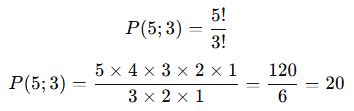
✅ Sonuç: Bu durumda 20 farklı sıralama mümkündür.

4. Tekrarlı Permütasyonun Kullanım Alanları

Tekrarlı permütasyon, özellikle farklı elemanların bir arada bulunduğu, ancak bazı elemanların aynı olduğu durumlarda kullanılır. Örnek kullanım alanları:

• Şifreleme sistemleri: Şifrelerde aynı harflerin tekrarı olabilir.
• Yarışmalar ve sıralamalar: Bazı yarışmalarda aynı skoru yapan yarışmacılar olabilir.
• Oturma düzenleri: Aynı türdeki koltukları yerleştirirken sıralamalar önemli olabilir.
• Anagramlar: Verilen harflerden oluşturulabilecek farklı kelimeler ve sıralamalar.

Özet

• Tekrarlı permütasyon kullanılırken tekrarlanan elemanlar dikkate alınır ve aynı elemanların sıralanması farklı bir permütasyon oluşturmaz.
• Formül:

​

• Örnek alanlar: Şifreleme, anagramlar, sıralamalar ve oturma düzenleri.

Sayı ve Kelime Oluşturma

Permütasyon kullanarak rakamlarla farklı sayılar ve harflerle farklı kelimeler oluşturabiliriz. Sıralama önemli olduğu için, permütasyon formüllerinden faydalanırız.

1. Farklı Rakamlarla Sayı Oluşturma

Örnek 1:
3, 4, 5, 6 rakamları kullanılarak 3 basamaklı kaç farklı sayı yazılabilir?

📌 Çözüm:

• Verilen rakamlar: 3, 4, 5, 6 (4 farklı rakam var)
• Sayı 3 basamaklı olacak → r=3

Formülü kullanalım:

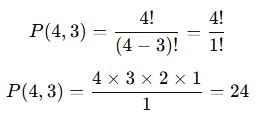
✅ Sonuç: 3, 4, 5, 6 rakamlarıyla 24 farklı 3 basamaklı sayı yazılabilir.

Örnek 2:
0, 1, 2, 3 rakamları kullanılarak 3 basamaklı kaç farklı sayı yazılabilir? (Başında 0 olamaz.)

📌 Çözüm:

• 0 ile başlayan sayılar 3 basamaklı olamaz, bu yüzden ilk basamak 0 olamaz!
• İlk basamak için 1, 2 veya 3 seçilebilir → 3 seçenek var
• İkinci basamak için 3 rakam kaldı
• Üçüncü basamak için 2 rakam kaldı

3×3×2=18

✅ Sonuç: Bu rakamlarla 18 farklı 3 basamaklı sayı oluşturulabilir.

2. Harflerle Kelime Oluşturma

Örnek 3:
“KALP” kelimesinin harfleri ile anlamlı ya da anlamsız kaç farklı kelime oluşturulabilir?

📌 Çözüm:

• 4 farklı harf var (K, A, L, P)
• 4 harf de kullanılacağı için:

✅ Sonuç: “KALP” kelimesinin harfleriyle 24 farklı kelime oluşturulabilir.

Örnek 4:
“BİLİM” kelimesinin harfleriyle kaç farklı kelime oluşturulabilir?

📌 Çözüm:

• Toplam harf sayısı = 5
• “İ” harfi 2 kez tekrar ediyor

Formülü uygulayalım:

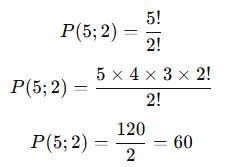
✅ Sonuç: “BİLİM” kelimesinin harfleriyle 60 farklı kelime oluşturulabilir.

3. Dikkat Edilmesi Gereken Noktalar

• Tekrarlı harfler varsa, tekrarlı permütasyon formülü kullanılır.
• Rakamlarla sayı oluşturulurken, başına 0 gelmemesi gerekiyorsa ilk basamak dikkatle seçilmelidir.

Özet

Kişilerin ve Nesnelerin Dizilişi

Bir grup insanın veya nesnenin belirli bir sıraya göre dizilmesi permütasyon kuralları ile hesaplanır. Sıra önemli olduğu için, farklı dizilişler farklı permütasyonlar oluşturur.

1. Farklı Kişilerin Yan Yana Dizilmesi

Bir grup insanın yan yana dizilme şekilleri, faktöriyel yöntemi ile hesaplanır.

Formül:

Burada $n$, dizilecek kişi veya nesne sayısını ifade eder.

📌 Örnek 1:
5 öğrenci bir sıraya kaç farklı şekilde dizilebilir?

✅ Sonuç: 5 öğrenci, 120 farklı şekilde sıralanabilir.

2. Belirli Kişiler Yan Yana Olmak Zorundaysa

Bazen bir gruptaki belirli kişiler mutlaka yan yana durmalıdır. Böyle durumlarda, o kişileri tek bir blok (grup) gibi düşünerek permütasyon hesaplarız.

📌 Örnek 2:
6 kişilik bir grupta Ali ve Ayşe her zaman yan yana olmak zorundadır. Grup kaç farklı şekilde sıralanabilir?

Çözüm:

• Ali ve Ayşe’yi tek bir kişi (blok) gibi düşünelim.
• Geriye kalan 4 kişi ile birlikte toplam 5 kişi varmış gibi olur.
• 5 kişinin sıralanma sayısı:

• Ali ve Ayşe kendi içlerinde yer değiştirebilir:

• Toplam sıralama:

✅ Sonuç: Ali ve Ayşe yan yana olmak koşuluyla, 6 kişi 240 farklı şekilde sıralanabilir.

3. Belirli Kişiler Yan Yana Gelmemek Zorundaysa

Eğer bazı kişiler yan yana gelmeyecekse, önce toplam permütasyonu hesaplar ve ardından yan yana oldukları durumları çıkarırız.

📌 Örnek 3:
7 kişilik bir grupta Hasan ve Zeynep asla yan yana durmamalıdır. Grup kaç farklı şekilde sıralanabilir?

Çözüm:

1. Tüm kişilerin sıralanma sayısı:

2. Hasan ve Zeynep yan yana olursa:

   • Hasan ve Zeynep tek kişi (blok) olarak düşünülür, yani 6 kişi varmış gibi olur.
   • 6 kişinin sıralanması:

   

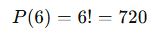
   • Hasan ve Zeynep kendi içlerinde yer değiştirebilir:

   

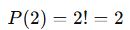
   • Toplam yan yana durumlar:

   

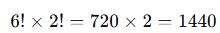
3. Yan yana olmama durumu:

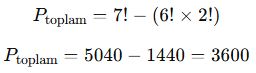
✅ Sonuç: Hasan ve Zeynep yan yana gelmeyecek şekilde 3600 farklı sıralama mümkündür.

4. Nesnelerin Dizilmesi ve Renkli Küpler Örneği

Eğer dizilmesi gereken nesneler benzer veya aynı tipte ise tekrarlı permütasyon kullanılır.

📌 Örnek 4:
Bir kutuda 3 kırmızı, 2 mavi ve 1 yeşil top bulunmaktadır. Bu toplar kaç farklı şekilde sıralanabilir?

Çözüm:

• Toplam 6 top var, ancak bazıları aynı renk olduğu için tekrarlı permütasyon formülü kullanılır:

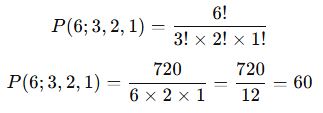
✅ Sonuç: Toplar 60 farklı şekilde sıralanabilir.

Özet

Dairesel Permütasyon

Dairesel permütasyon, nesnelerin veya kişilerin bir çember etrafında sıralanmasını ifade eder. Lineer (düz sıra) permütasyondan farklı olarak, çemberde başlangıç noktası olmadığı için bir elemanın sabit tutulup diğerlerinin sıralanmasıyla hesaplanır.

1. Dairesel Permütasyon Formülü

Bir çember etrafında $n$ tane farklı nesne veya kişi sıralanacaksa, bu nesnelerin sıralama sayısı şu formülle bulunur:

Burada:

• n → Çember etrafında dizilecek nesne veya kişi sayısı
• (n−1)! → İlk elemanı sabit kabul edip geri kalanları sıralama

2. Örnek 1: Çember Etrafında Kişi Dizme

📌 Örnek:
6 kişi yuvarlak bir masaya kaç farklı şekilde oturabilir?

📌 Çözüm:

• n=6
• Dairesel permütasyon formülünü kullanarak:

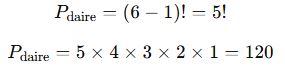
✅ Sonuç: 6 kişi yuvarlak bir masada 120 farklı şekilde oturabilir.

3. Örnek 2: Bilezik veya Halka Üzerinde Renkli Boncuk Dizme

📌 Örnek:
Bir bilezik üzerine 7 farklı renkli boncuk kaç farklı şekilde dizilebilir?

📌 Çözüm:

✅ Sonuç: 7 farklı renkli boncuk, simetri dikkate alındığında 360 farklı şekilde dizilebilir.

4. Örnek 3: Belirli Kişiler Yan Yana Oturacaksa

📌 Örnek:
8 kişi yuvarlak bir masada oturacaktır. Ancak Ahmet ve Zeynep her zaman yan yana oturmak zorundadır. Kaç farklı oturma düzeni oluşturulabilir?

📌 Çözüm:

✅ Sonuç: Ahmet ve Zeynep yan yana olacak şekilde 1440 farklı oturma düzeni oluşturulabilir.

5. Dairesel Permütasyon Kullanım Alanları

Dairesel permütasyon günlük hayatta birçok alanda karşımıza çıkar:

• Yuvarlak masa oturma düzenleri
• Bilezik, halhal ve kolye tasarımları
• Çarklar ve dişlilerin düzenlenmesi
• DNA dizilim analizleri
• Özel davetlerde oturma planları

Özet Tablo

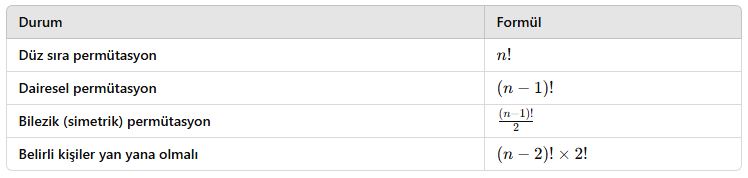
Kombinasyon

Kombinasyon Tanımı

Kombinasyon, belirli sayıda nesnenin veya kişinin, sırasız şekilde seçilmesini ifade eder. Permütasyondan farklı olarak sıralama önemli değildir, sadece seçim yapılır.

📌 Örnek:
Bir spor takımının 5 kişilik bir kadrosu vardır. 3 kişi seçilecekse:

• Kimin önce seçildiği önemli değildir.
• Sadece hangi 3 kişinin seçildiği önemlidir.
• Bu bir kombinasyon problemidir.

1. Kombinasyon Formülü

Eğer bir kümede $n$ farklı nesne varsa ve bunlardan $r$ tanesi seçiliyorsa, kombinasyon şu formülle hesaplanır:

​

Burada:

• n → Toplam eleman sayısı
• r → Seçilecek eleman sayısı
• ! (faktöriyel) → Bir sayının kendisinden küçük bütün pozitif tam sayılarla çarpımıdır.

2. Örnekler ve Çözümleri

Örnek 1: Bir Takım Seçme

📌 Örnek:
10 kişilik bir sınıftan 4 kişilik bir ekip kaç farklı şekilde seçilebilir?

📌 Çözüm:

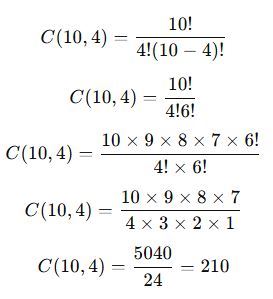
✅ Sonuç: 10 kişiden 4 kişilik bir ekip 210 farklı şekilde seçilebilir.

Örnek 2: Komisyon Seçimi

📌 Örnek:
8 kişilik bir gruptan 3 kişi seçilerek bir komisyon oluşturulacaktır. Kaç farklı seçim yapılabilir?

📌 Çözüm:

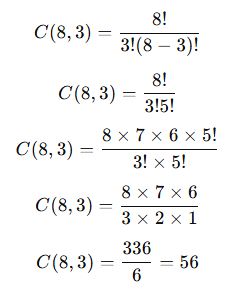
✅ Sonuç: 8 kişiden 3 kişilik bir komisyon 56 farklı şekilde seçilebilir.

3. Kombinasyon ile Permütasyon Arasındaki Farklar

4. Kombinasyonun Kullanım Alanları

• Öğrenci grubu seçimi (Sınıftan kaç farklı grup oluşturulabilir?)
• Komisyon veya jüri seçimi (Hangi kişiler jüri olabilir?)
• Loto veya piyango çekilişi (Kazanan numaralar nasıl seçilir?)
• Kimyasal bileşikler oluşturma (Belirli elementlerden kaç farklı bileşik yapılabilir?)
• Yemek kombinasyonları (Menüde hangi yemekler birlikte seçilebilir?)

5. Özet

• Kombinasyon, sırasız seçimdir ve C(n,r) formülüyle hesaplanır.
• Kombinasyon ile permütasyon farkı: Permütasyonda sıralama önemliyken kombinasyonda yalnızca seçim yapılır.
• Kombinasyon, grup oluşturma, jüri seçimi ve loto çekilişi gibi durumlarda kullanılır.

Bir Örnekle Kombinasyon

Kombinasyon, belirli sayıda nesne veya kişinin, sıralama olmadan seçilmesi anlamına gelir. Şimdi bu kavramı günlük hayattan örneklerle daha iyi anlayalım.

1. Örnek 1: Bir Takımdan Oyuncu Seçme

📌 Soru:
12 kişilik bir futbol takımından 5 oyuncu seçilecektir. Kaç farklı seçim yapılabilir?

📌 Çözüm:

• Toplam oyuncu sayısı: n=12
• Seçilecek oyuncu sayısı: r=5

Formülü kullanalım:

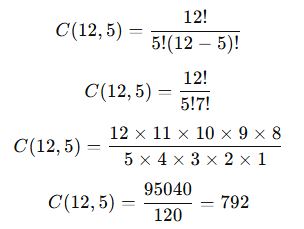
✅ Sonuç: 12 oyuncu arasından 5 kişilik bir takım 792 farklı şekilde oluşturulabilir.

2. Örnek 2: Bir Yarışmada Jüri Seçimi

📌 Soru:
10 kişilik bir gruptan 3 kişi jüri olarak seçilecektir. Kaç farklı jüri oluşturulabilir?

📌 Çözüm:

• Toplam kişi sayısı: n=10
• Seçilecek jüri sayısı: r=3

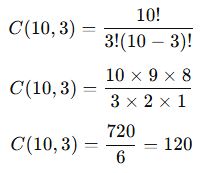
✅ Sonuç: 10 kişi arasından 3 kişilik jüri 120 farklı şekilde seçilebilir.

3. Örnek 3: Loto Sayıları

📌 Soru:
49 farklı numara arasından 6 numara çekilen bir loto oyununda, kaç farklı kombinasyon mümkündür?

📌 Çözüm:

• Toplam numara sayısı: n=49
• Seçilecek numara sayısı: r=6

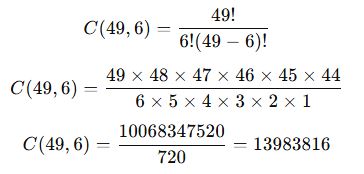
✅ Sonuç: 49 numara arasından 6 numara seçildiğinde, toplamda 13.983.816 farklı kombinasyon mümkündür.

4. Örnek 4: Kimyasal Bileşikler Oluşturma

📌 Soru:
Bir laboratuvarda 7 farklı kimyasal madde bulunmaktadır. Bu maddelerden 4 tanesi karıştırılarak yeni bir bileşik oluşturulacaktır. Kaç farklı bileşik yapılabilir?

📌 Çözüm:

• Toplam madde sayısı: n=7
• Seçilecek madde sayısı: r=4

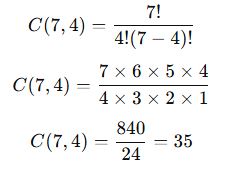
✅ Sonuç: 7 madde arasından 4 tanesi seçilerek 35 farklı bileşik oluşturulabilir.

5. Özet

• Kombinasyon, sıralamanın önemli olmadığı seçimlerde kullanılır.
• Formül:

​

• Kombinasyon kullanımı gereken durumlar:
  ✅ Takım seçimi
  ✅ Jüri veya komisyon belirleme
  ✅ Loto veya piyango çekilişleri
  ✅ Kimyasal bileşikler oluşturma

Kombinasyon Yöntemleri

Kombinasyon, sıralamanın önemli olmadığı seçimlerde kullanılan bir yöntemdir. Farklı problemlerde kombinasyon hesaplamalarını hızlı ve doğru yapmak için çeşitli yöntemler geliştirilmiştir.

1. Temel Kombinasyon Formülü

Bir kümede n farklı nesne varsa ve bunlardan r tanesi seçiliyorsa:

​

Bu formül, seçim işlemi için temel yöntemdir. Ancak bazı özel durumlarda farklı hesaplama teknikleri kullanılabilir.

2. Özellikler ve Kolaylaştırıcı Yöntemler

1️⃣ Simetri Özelliği (Dönüşüm Kuralı)

Bu özellik sayesinde, küçük değerlerle hesaplama yaparak işlem kolaylaştırılabilir.

📌 Örnek:

Çünkü 7 eleman seçmek yerine 3 eleman seçilmeyenleri bulmak daha kolay olabilir.

✅ Sonuç:

2️⃣ Kombinasyonun Faktöriyel Açılımı ile Hesaplanması

Bazı durumlarda kombinasyonun faktöriyel açılımını sadeleştirerek işlem kolaylaştırılabilir.

📌 Örnek:

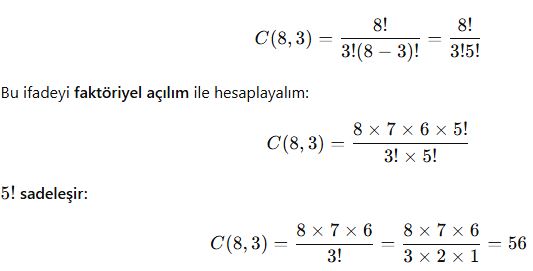
✅ Sonuç: 8 kişiden 3 kişi 56 farklı şekilde seçilebilir.

3️⃣ Özel Değerler İçin Kombinasyon Kısayolları

• C(n,0)=1 → Boş küme sadece 1 şekilde seçilebilir.
• C(n,1)=n → Bir eleman seçmek, n farklı şekilde yapılabilir.
• C(n,n)=1 → Tüm elemanları seçmek sadece 1 şekilde mümkündür.
• C(n,n−1)=n → N elemandan 1 tanesi dışarıda bırakılırsa, kalanların seçimi n farklı şekilde olur.

📌 Örnek:

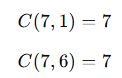
✅ Sonuç: 7 kişiden 6 kişi seçmek, sadece 1 kişiyi dışarıda bırakmak olduğu için 7 farklı şekilde yapılabilir.

4️⃣ Pascal Üçgeni Kullanımı

Pascal Üçgeni, kombinasyon hesaplamalarını hızlı yapmak için kullanılan bir yöntemdir. Üçgen şu kurala dayanır:

📌 Örnek:

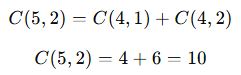
Bu yöntem özellikle küçük değerlerde hesaplamaları hızlandırır.

3. Kombinasyon Hesaplamalarında Kullanım Kolaylıkları

🔹 Simetri kuralını kullanarak büyük sayılar yerine küçükleri tercih edin.
🔹 Faktöriyel sadeleştirme ile büyük çarpımları minimize edin.
🔹 Pascal Üçgeni ile küçük kombinasyon değerlerini hızlı hesaplayın.
🔹 Özel değerler ve kısayolları akılda tutarak hesaplama sürecini hızlandırın.

4. Özet Tablo

Kişilerin Seçimi

Kombinasyonun en yaygın kullanım alanlarından biri, belirli sayıda kişiyi seçme problemleridir. Sıralamanın önemli olmadığı durumlarda, kombinasyon formülü kullanılır.

​

Burada:

• n → Toplam kişi sayısı
• r → Seçilecek kişi sayısı

Şimdi farklı senaryoları inceleyelim.

1. Temel Kişi Seçme Problemleri

📌 Örnek 1:
12 kişilik bir gruptan 4 kişi kaç farklı şekilde seçilebilir?

📌 Çözüm:

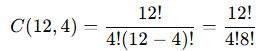
Faktöriyel sadeleştirme yapalım:

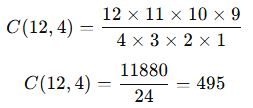
✅ Sonuç: 12 kişilik bir gruptan 4 kişi 495 farklı şekilde seçilebilir.

2. Belirli Bir Kişinin Seçilmesi veya Seçilmeme Durumu

Bazı sorularda, belirli bir kişinin seçildiği veya seçilmediği durumlar olabilir.

📌 Örnek 2:
Bir ekip 8 kişiden oluşmaktadır. 3 kişi seçilecek, ancak Ahmet mutlaka seçilecektir. Kaç farklı seçim yapılabilir?

📌 Çözüm:

• Ahmet zaten seçildiği için, geriye kalan 7 kişiden 2 kişi daha seçmemiz gerekir.
• Bu durumda:

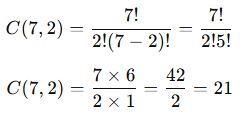
✅ Sonuç: Ahmet’in dahil olduğu 21 farklı ekip oluşturulabilir.

📌 Örnek 3:
Bir ekip 10 kişiden oluşmaktadır. 4 kişi seçilecek, ancak Ayşe bu ekibe alınmayacaktır. Kaç farklı seçim yapılabilir?

📌 Çözüm:

• Ayşe seçilmeyeceği için, geriye kalan 9 kişiden 4 kişi seçmemiz gerekir.
• Bu durumda:

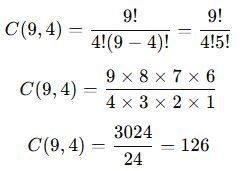
✅ Sonuç: Ayşe’nin olmadığı 126 farklı ekip oluşturulabilir.

3. Belirli Kişilerin Birlikte veya Ayrı Seçilme Durumu

Eğer belirli kişiler her zaman birlikte seçilecekse, onları tek bir kişi gibi düşünebiliriz. Eğer belirli kişiler birlikte seçilmeyecekse, tüm olasılıklardan bu durumları çıkarabiliriz.

📌 Örnek 4:
Bir grupta 8 kişi vardır. 4 kişilik bir ekip oluşturulacaktır. Ancak Can ve Deniz her zaman birlikte seçilmelidir. Kaç farklı ekip kurulabilir?

📌 Çözüm:

• Can ve Deniz’i tek bir kişi gibi düşünelim.
• Geriye kalan 6 kişiden 2 kişi daha seçmemiz gerekir.
• Yani 6 kişiden 2 kişi seçme problemi olur:

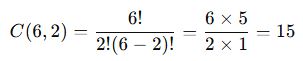
✅ Sonuç: Can ve Deniz’in daima birlikte olduğu 15 farklı ekip oluşturulabilir.

📌 Örnek 5:
Bir grupta 7 kişi vardır. 3 kişilik bir ekip oluşturulacaktır. Ancak Ali ve Veli hiçbir zaman birlikte seçilmeyecektir. Kaç farklı seçim yapılabilir?

📌 Çözüm:
1️⃣ Önce tüm olasılıkları hesaplayalım:

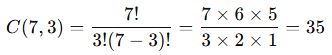
2️⃣ Şimdi Ali ve Veli’nin birlikte olduğu durumları çıkaralım.

• Ali ve Veli birlikte seçilmişse, 7 kişiden geriye 5 kişi kalır, ve bu 5 kişiden 1 kişi daha seçmemiz gerekir:

3️⃣ Son olarak tüm seçimlerden Ali ve Veli’nin birlikte olduğu durumları çıkaralım:

✅ Sonuç: Ali ve Veli’nin birlikte olmadığı 30 farklı ekip kurulabilir.

4. Özet Tablo

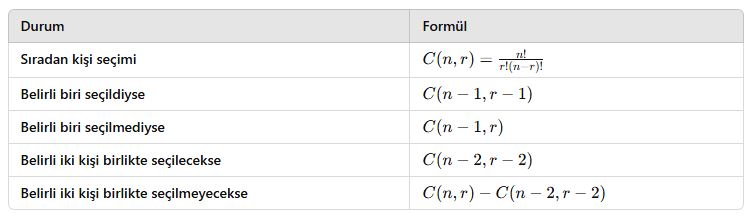
5. Sonuç

• Kişi seçme problemlerinde kombinasyon kullanılır çünkü sıralama önemli değildir.
• Özel durumlar (belirli kişilerin seçilmesi, seçilmemesi veya birlikte olmaması) doğru yöntemle çözülmelidir.
• Kombinasyonun özellikleri kullanılarak hesaplamalar kolaylaştırılabilir.

Nesnelerin Seçimi

Kombinasyon sadece kişiler için değil, aynı zamanda farklı nesnelerin seçilmesi için de kullanılır. Nesnelerin seçimi problemlerinde sıralamanın önemli olmadığı durumlar için kombinasyon kullanılır.

1. Temel Nesne Seçimi

📌 Örnek 1:
Bir markette 6 farklı içecek vardır. Bu içeceklerden 3 tanesi seçilecektir. Kaç farklı seçim yapılabilir?

📌 Çözüm:

• Toplam içecek sayısı: n=6
• Seçilecek içecek sayısı: r=3

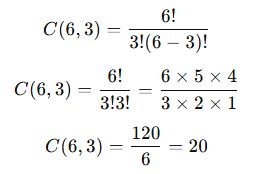
✅ Sonuç: 6 içecekten 3 tanesi 20 farklı şekilde seçilebilir.

2. Belirli Nesnelerin Seçildiği veya Seçilmediği Durumlar

📌 Örnek 2:
Bir kütüphanede 8 farklı kitap vardır. 4 kitap seçilecek, ancak “Matematik” kitabı mutlaka seçilecektir. Kaç farklı seçim yapılabilir?

📌 Çözüm:

• Matematik kitabı kesin seçildiğine göre, geriye kalan 7 kitaptan 3 kitap daha seçmeliyiz.

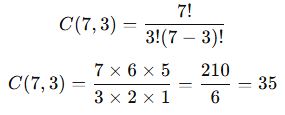
✅ Sonuç: Matematik kitabı dahil edilerek 35 farklı seçim yapılabilir.

📌 Örnek 3:
10 farklı çiçek türü bulunan bir bahçede, 5 çiçek türü seçilecektir. Ancak “Gül” kesinlikle seçilmeyecektir. Kaç farklı seçim yapılabilir?

📌 Çözüm:

• Gül seçilmeyeceği için, seçim 9 çiçek arasından yapılacaktır.

✅ Sonuç: Gülün olmadığı 126 farklı çiçek seçimi yapılabilir.

3. Aynı Türden Nesnelerin Seçimi (Tekrarlı Kombinasyon)

Bazen seçim yapılacak nesneler birbirinden farklı değil, aynı olabilir. Bu tür problemlerde tekrarlı kombinasyon kullanılır.

📌 Örnek 4:
Bir markette 4 farklı meyve vardır: Elma, Muz, Portakal, Çilek. Müşteri toplam 6 meyve alacaktır. Kaç farklı seçim mümkündür?

📌 Çözüm:

• Meyveler birbirinden farklı değil, aynı türden oldukları için tekrarlı kombinasyon kullanılır.
• Formül:

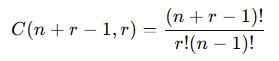
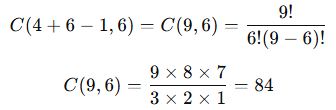
✅ Sonuç: 4 farklı meyveden 6 tane seçerken 84 farklı kombinasyon mümkündür.

4. Özet Tablo

5. Sonuç

• Nesne seçimi problemlerinde sıralama önemli değilse kombinasyon kullanılır.
• Bazı nesneler kesinlikle seçilecek veya seçilmeyecekse, problem ona göre çözümlenir.
• Aynı türden nesneler seçiliyorsa tekrarlı kombinasyon formülü kullanılır.

Kümelerde Kombinasyon

Kombinasyon, kümelerle ilgili problemlerde sıklıkla kullanılır. Bir kümenin alt kümelerini oluşturma, belirli elemanları içeren veya içermeyen alt kümeleri bulma gibi birçok durumda kombinasyon yöntemleri kullanılır.

1. Bir Kümenin Alt Küme Sayısı

Eğer n elemanlı bir küme varsa, bu kümenin alt küme sayısı şu formülle hesaplanır:

✅ Sonuç: 5 elemanlı bir kümenin 32 alt kümesi vardır.

2. r Elemanlı Alt Küme Sayısı (Kombinasyon Kullanımı)

Eğer n elemanlı bir kümeden r elemanlı alt kümeler oluşturulacaksa, kombinasyon formülü kullanılır:

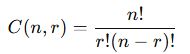
📌 Örnek 2:
7 elemanlı bir kümeden 3 elemanlı kaç farklı alt küme oluşturulabilir?

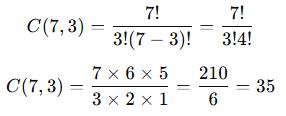
✅ Sonuç: 7 elemanlı bir kümeden 3 elemanlı 35 farklı alt küme oluşturulabilir.

3. Belirli Elemanları İçeren veya İçermeyen Alt Küme Sayısı

Bazı durumlarda belirli elemanların seçildiği veya seçilmediği alt kümeleri bulmamız gerekir.

📌 Örnek 3:
6 elemanlı bir kümenin, A elemanını mutlaka içeren kaç farklı 4 elemanlı alt kümesi vardır?

📌 Çözüm:

• A zaten seçildiğine göre, geriye kalan 5 elemandan 3’ü seçilmelidir.
• Bu yüzden problem C(5,3) kombinasyonuna dönüşür.

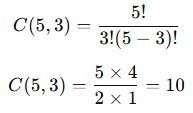
✅ Sonuç: A elemanını içeren 10 farklı alt küme oluşturulabilir.

📌 Örnek 4:
6 elemanlı bir kümenin, B ve C elemanlarını içermeyen kaç farklı 3 elemanlı alt kümesi vardır?

📌 Çözüm:

• B ve C elemanları seçilmeyecekse, geriye 4 eleman kalır.
• Bu 4 elemandan 3’ü seçilecektir.

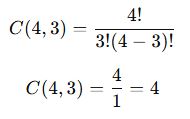
✅ Sonuç: B ve C’yi içermeyen 4 farklı alt küme oluşturulabilir.

4. Kesişim ve Birleşim Alt Küme Problemleri

Eğer bir kümenin alt kümeleri arasında kesişim veya birleşimle ilgili sorular varsa, kombinasyon formülü kullanılarak çözüm yapılır.

📌 Örnek 5:
Bir kümede 8 eleman vardır. En az 2 eleman içeren kaç farklı alt küme vardır?

📌 Çözüm:

• Tüm alt kümelerin sayısı:
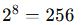
• Boş küme ve tek elemanlı kümeleri çıkaralım:
  • Boş küme: 1 tane
  • Tek elemanlı kümeler: C(8,1)=8
• Sonuç:

✅ Sonuç: En az 2 eleman içeren 247 farklı alt küme vardır.

5. Özet Tablo

6. Sonuç

• Bir kümenin alt küme sayısı 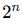 ile hesaplanır.
• Belirli eleman sayısına sahip alt kümeler için kombinasyon formülü kullanılır.
• Özel durumlarda (belirli elemanları içeren veya içermeyen alt kümeler), uygun kombinasyon hesaplamaları yapılmalıdır.

Geometrik Kombinasyon

Geometrik kombinasyon, geometri ile ilgili problemlerde kombinasyon kullanımı anlamına gelir. Bu tür sorular genellikle doğrular, üçgenler, dörtgenler ve uzaydaki noktalar arasındaki seçimleri içerir.

1. Noktalardan Doğru Parçaları Seçme

Bir düzlemde veya uzayda verilen $n$ farklı noktadan kaç farklı doğru çizilebileceğini bulmak için 2 nokta seçme kombinasyonu kullanılır.

📌 Formül:

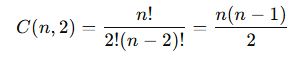
📌 Örnek 1:
Bir düzlemde 6 farklı nokta bulunmaktadır. Bu noktalar kaç farklı doğru oluşturabilir?

📌 Çözüm:

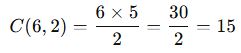
✅ Sonuç: 6 noktadan 15 farklı doğru çizilebilir.

2. Noktalardan Üçgen Oluşturma

Üçgen oluşturmak için 3 farklı nokta seçilmelidir.

📌 Formül:

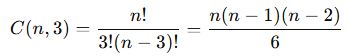
📌 Örnek 2:
Bir düzlemde 7 farklı nokta bulunmaktadır. Kaç farklı üçgen oluşturulabilir?

📌 Çözüm:

✅ Sonuç: 7 noktadan 35 farklı üçgen oluşturulabilir.

🔹 Özel Durum:

• Eğer noktalar doğrusal ise, üçgen oluşmaz!
• Doğrusal olmayan 7 noktadan üçgen oluşturuluyorsa, yukarıdaki formül kullanılır.

3. Dörtgen ve Çokgen Oluşturma

Düzlemdeki $n$ nokta ile dörtgen veya çokgen oluşturmak için uygun sayıda nokta seçilir.

📌 Dörtgen oluşturma formülü:

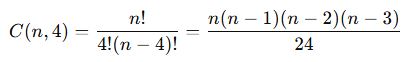
📌 Örnek 3:
Bir düzlemde 8 farklı nokta vardır. Kaç farklı dörtgen oluşturulabilir?

📌 Çözüm:

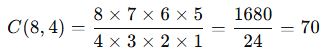
✅ Sonuç: 8 noktadan 70 farklı dörtgen oluşturulabilir.

📌 Genel Çokgen Formülü:

✅ Sonuç: 6 noktadan sadece 6 farklı beşgen oluşturulabilir.

4. İç ve Dış Noktaları Kullanarak Çokgenler

Eğer bir düzlemde bazı noktalar içeride, bazıları dışarıda bulunuyorsa:

• İç noktalar dörtgen oluşturmada kullanılabilir mi?
• Dış noktalar yalnızca kenarlarda mı yer alacak?

📌 Örnek 4:
Bir düzlemde 10 nokta var. Bunların 4’ü aynı doğru üzerinde. Kaç farklı üçgen oluşturulabilir?

📌 Çözüm:

Tüm noktalardan üçgen oluşturma:

Ancak 4 nokta doğrusal olduğu için, bunlarla üçgen oluşturulamaz:

Sonuç:

✅ Sonuç: Bu durumda 116 farklı üçgen oluşturulabilir.

5. Özet Tablo

6. Sonuç

• Geometrik kombinasyon, noktalardan doğru, üçgen, dörtgen ve çokgenler oluşturma problemlerinde kullanılır.
• Noktaların doğrusal olup olmadığına dikkat edilmelidir.
• Özel durumlarda doğrusal noktalar çıkarılarak doğru sonuç bulunur.

PERMÜTASYON VE KOMBİNASYON TESTİ

1. Aşağıdaki durumların hangisinde permütasyon kullanılır?

A) 5 farklı renkten 3’ünü seçip bayrak oluşturma
B) 6 kişilik bir gruptan 4 kişilik komite oluşturma
C) 10 farklı kitabı bir rafa dizme
D) 8 kişilik bir gruptan 2 kişilik takım oluşturma

2. Aşağıdaki işlemlerden hangisinin sonucu 210’dur?

3. 8 kişi bir sıraya kaç farklı şekilde dizilebilir?

A) 40,320
B) 5,040
C) 720
D) 256

4. 12 kişilik bir gruptan 5 kişilik bir takım kaç farklı şekilde seçilebilir?

A) 792
B) 8,000
C) 950
D) 1,680

5. Bir torbada 7 farklı top vardır. Bunlardan 3’ü seçilip sıralanacaktır. Kaç farklı sıralama yapılabilir?

A) 210
B) 35
C) 840
D) 420

6. 9 farklı harften 4 harf seçilerek bir kelime oluşturulacaktır. Kaç farklı sıralama mümkündür?

A) 3,024
B) 126
C) 302
D) 720

7. 5 farklı meyveden 3’ü seçilecektir. Kaç farklı seçim yapılabilir?

A) 10
B) 20
C) 30
D) 60

8. 10 farklı kişi arasından 3 kişilik bir jüri seçilecektir. Kaç farklı seçim mümkündür?

A) 30
B) 120
C) 720
D) 100

9. Bir sınıfta 6 erkek, 4 kız öğrenci bulunmaktadır. 3 kişilik bir ekip oluşturulacak, ancak bu ekipte en az 1 kız bulunacaktır. Kaç farklı seçim yapılabilir?

A) 64
B) 70
C) 80
D) 90

10. 8 nokta ile kaç farklı doğru çizilebilir?

A) 56
B) 28
C) 16
D) 8

CEVAP ANAHTARI

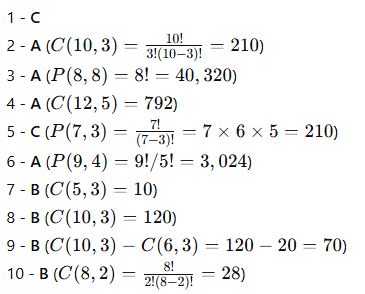
📚 Bu test, permütasyon ve kombinasyon kavramlarını pekiştirmenizi sağlayacak! 🚀 Yanıtlarınızı kontrol edip eksiklerinizi belirleyebilirsiniz. 🎯