İçindekiler
TYT Matematik Polinomlar Konu Anlatımı
Matematikte cebirsel ifadelerle işlem yaparken, özel bir yapıya sahip olan polinomlar, sayısal ve değişkenli ifadelerin düzenli bir formda yazılmasını sağlayan önemli matematiksel kavramlardan biridir. Polinomlar, değişkenler ve katsayılar kullanılarak oluşturulan ifadeler olup, toplama, çıkarma ve çarpma gibi temel işlemlere karşı kapalıdır. Bu nedenle, polinomlar, matematiğin pek çok alanında olduğu gibi mühendislik, fizik, ekonomi ve bilgisayar bilimlerinde de yaygın olarak kullanılmaktadır. TYT Matematik kapsamında, polinomların temel özellikleri, işlem kuralları ve grafik yorumlamaları oldukça önemlidir.
Bu ünitede, öncelikle polinomların temel tanımını, derecesini, türlerini ve özelliklerini ele alacağız. Ardından, polinomlarla işlem yapmayı, bölme ve bölünebilme kurallarını detaylandıracağız. Ayrıca, özel polinom türleri olan çarpanlara ayırma tekniklerini ve polinom eşitliklerini inceleyeceğiz. Konunun sonunda, öğrendiğimiz bilgileri pekiştirmek adına çeşitli örnek sorular çözecek ve ünitenin tamamını kapsayan 10 soruluk bir test ile bilgimizi değerlendireceğiz. Şimdi, polinomların temel tanımıyla başlayalım.
Polinom Nedir? Tanımı ve Temel Kavramlar
Matematikte polinom, değişkenler ve katsayılar kullanılarak oluşturulan cebirsel ifadelerden biridir. Polinomlar, toplama, çıkarma ve çarpma işlemlerine kapalıdır, ancak değişkenin üsleri yalnızca pozitif tam sayı olabilir. İçinde köklü ifadeler, kesirli üsler veya negatif üsler bulunan ifadeler polinom değildir.
Bir polinom genel olarak şu şekilde ifade edilir:

Polinomlarda Temel Kavramlar
-
Terimler ve Katsayılar
- Her polinom, terimlerden oluşur. Örneğin,
 polinomunda 4x³, -2x ve 7 birer terimdir.
polinomunda 4x³, -2x ve 7 birer terimdir. - Katsayılar: 4, -2 ve 7’dir.
- Sabit terim: Değişken içermeyen sayı (7)’dir.
- Her polinom, terimlerden oluşur. Örneğin,
-
Polinomun Derecesi
- Bir polinomun derecesi, içindeki en yüksek üslü terimin derecesidir.
- Örnek:
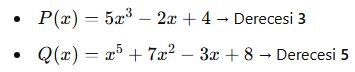
-
Sabit Polinom ve Sıfır Polinomu
- Sabit Polinom: Değişken içermeyen, yalnızca sabit bir sayıdan oluşan polinomdur (örneğin,
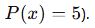
- Sıfır Polinomu: Tüm katsayıları sıfır olan polinomdur
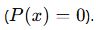 Derecesi tanımsızdır.
Derecesi tanımsızdır.
- Sabit Polinom: Değişken içermeyen, yalnızca sabit bir sayıdan oluşan polinomdur (örneğin,
Polinomlarda İşlemler (Toplama, Çıkarma, Çarpma)
Polinomlarla işlem yaparken, toplama, çıkarma ve çarpma işlemleri belirli kurallar çerçevesinde yapılır. Bu işlemler, polinomların derecelerini değiştirebilir ve polinomun genel yapısını etkileyebilir. Şimdi bu işlemleri detaylıca ele alalım.
1. Polinomlarda Toplama ve Çıkarma İşlemi
Polinomları toplarken veya çıkarırken, benzer terimler birbiriyle işlem görür. Benzer terimler, değişkenin üssü aynı olan terimlerdir.
Örnek 1: Toplama İşlemi
Aşağıdaki iki polinomu toplayalım:
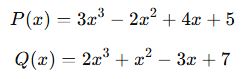

![]()
Örnek 2: Çıkarma İşlemi
Aynı polinomları birbirinden çıkaralım:
![]()
İşlem adımları:

![]()
2. Polinomlarda Çarpma İşlemi
Polinomlar çarpılırken her terim, diğer polinomdaki tüm terimlerle çarpılır. Çarpma işlemi dağılım özelliği kullanılarak yapılır.
Örnek 3: Bir Terimli Polinom ile Çarpma
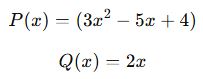
Her terim 2x ile çarpılır:
![]()
Sonuç:
![]()
Örnek 4: İki Polinomun Çarpımı
![]()
Dağılma özelliğini kullanarak:
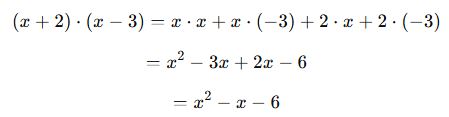
Bu tür çarpma işlemleri, ilerleyen konularda çarpanlara ayırma konusunda da sıkça kullanılacaktır.
Polinomların Derecesi ve Terimleri
Polinomların derecesi ve terimleri, polinomları anlamak ve işlem yapmak için oldukça önemlidir. Bir polinomun derecesi, içindeki en büyük üslü terimin derecesidir. Ayrıca, polinomun her bir bileşeni de terim olarak adlandırılır. Şimdi bu kavramları detaylıca ele alalım.
1. Polinomun Derecesi (deg P(x))
Bir polinomun derecesi, polinomda bulunan en büyük üslü terimin üssüne eşittir. Dereceyi bulmak için en yüksek dereceli terimi belirlemek yeterlidir.
Örnek 1:
![]()
Bu polinomda en büyük üs 5 olduğundan, polinomun derecesi:
![]()
Örnek 2:
![]()
Bu polinomda en büyük üs 7 olduğundan, polinomun derecesi:
![]()
Eğer polinom sabit bir sayıdan oluşuyorsa ![]() derecesi sıfırdır.
derecesi sıfırdır.
2. Polinomun Terimleri
Polinomdaki her bir çarpanı içeren ifadeye terim denir. Her terimin katsayısı ve değişkeni bulunur.
Örnek 3:
Polinom:
![]()
Bu polinomun terimleri şunlardır:
- 6x⁴ → 4. dereceden bir terim
- -3x² → 2. dereceden bir terim
- 2x → 1. dereceden bir terim
- -5 → Sabit terim
Her terimin katsayısı, başındaki çarpan değeridir:
- 6x⁴’ün katsayısı 6
- -3x²’nin katsayısı -3
- 2x’in katsayısı 2
- -5’in katsayısı -5
3. Polinomun Baş Katsayısı ve Sabit Terimi
- Baş katsayı: Polinomun en yüksek dereceli teriminin katsayısıdır.
- Sabit terim: İçinde değişken bulunmayan, yalnızca sayıdan oluşan terimdir.
Örnek 4:
![]()
- Baş katsayı = 7 (çünkü en büyük üslü terimin katsayısı 7’dir)
- Sabit terim = -2
Özel Durumlar:
-
Sabit Polinomlar:
- İçinde değişken olmayan polinomlardır. Örneğin:
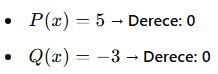
- İçinde değişken olmayan polinomlardır. Örneğin:
-
Sıfır Polinomu:
- Tüm katsayıları 0 olan polinomdur:
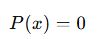
- Derecesi tanımsızdır.
- Tüm katsayıları 0 olan polinomdur:
Polinomların Özellikleri ve Türleri
Polinomlar, sahip oldukları özelliklere ve biçimlerine göre farklı türlere ayrılır. Bu türlerin anlaşılması, polinomlarla işlem yapmayı kolaylaştırır ve ileri seviye matematik konularında büyük önem taşır. Şimdi, polinomların temel özelliklerini ve türlerini inceleyelim.
1. Polinomların Özellikleri
Bir polinomun sahip olduğu bazı temel özellikler şunlardır:
-
Polinomlarda değişkenin üssü negatif veya kesirli olamaz.
Örnek:
-
Bir polinomun derecesi, en büyük üslü terimin derecesidir.
Örnek:
Bu polinomun derecesi 4’tür.
-
Polinomlarda katsayılar herhangi bir reel sayı olabilir.
-
Örnek:
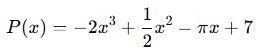
Burada katsayılar (-2, 1/2, -π, 7) reel sayılardır.
-
Polinomlar toplama, çıkarma ve çarpma işlemlerine kapalıdır.
Ancak bölme işlemi her zaman polinom vermez.
2. Polinom Türleri
Polinomlar, derecelerine ve yapılarına göre farklı gruplara ayrılır.
a) Derecelerine Göre Polinom Türleri
-
Sabit Polinom
- Hiçbir değişken içermeyen polinomlardır.
- Örnek:
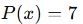
- Derecesi 0’dır.
-
Doğrusal Polinom (Birinci Dereceden Polinom)
- En yüksek dereceli terimi x¹ olan polinomlardır.
- Genel form:
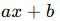
- Örnek:
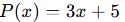
- Derecesi 1’dir.
-
İkinci Derece Polinom (Kare Polinom)
- En büyük üssü 2 olan polinomlardır.
- Genel form:
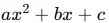
- Örnek:
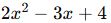
- Derecesi 2’dir.
-
Üçüncü Derece Polinom (Küp Polinom)
- En büyük üssü 3 olan polinomlardır.
- Genel form:
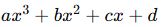
- Örnek:
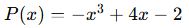
- Derecesi 3’tür.
-
Dördüncü ve Daha Büyük Dereceli Polinomlar
- En büyük üssü 4 veya daha büyük olan polinomlar bu grupta incelenir.
- Örnek:
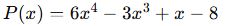
- Derecesi 4’tür.
b) Özel Polinom Türleri
-
Tek ve Çift Polinomlar
- Bir polinomdaki tüm terimlerin üssü tek ise, polinom tek polinomdur.
- Tüm terimlerin üssü çift ise, polinom çift polinomdur.
- Örnekler:
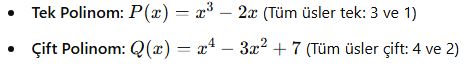
-
Sıfır Polinomu
- Tüm katsayıları sıfır olan polinomdur.
- Örnek:
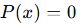
- Derecesi tanımsızdır.
-
Birim Polinom (Monom)
- Tek bir terimden oluşan polinomlara denir.
- Örnek:
-
İkili Polinom (Binom)
- İki terimli polinomlardır.
- Örnek:

-
Üçlü Polinom (Trinom)
- Üç terimli polinomlardır.
- Örnek:
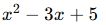
Polinom Bölme İşlemi ve Bölünebilme Kuralları
Polinom bölme işlemi, bir polinomu başka bir polinoma bölerek elde edilen bölüm ve kalan polinomları bulma işlemidir. Bu işlem, sayı bölmesine benzer şekilde yapılır ancak terimler arasında dereceler dikkate alınarak işlem yapılır.
1. Polinom Bölme İşlemi
Bölme işlemi şu şekilde gösterilir:
![]()
Burada:

Polinom bölme işleminde, kalanın derecesi bölenin derecesinden küçük olmak zorundadır. Eğer kalan sıfır olursa, P(x), D(x) polinomuna tam bölünmüş demektir.
2. Örnek: Bir Polinomu Bir Terimli Polinoma Bölme
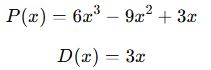
Bu ifadeyi terim terim bölelim:
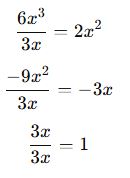
Sonuç:
![]()
Bu işlemde kalan sıfır olduğundan, polinom tam bölünmüştür.
3. Örnek: Bir Polinomu Bir Polinoma Bölme (Uzun Bölme Yöntemi)
Polinom bölme işlemi, sayılarda yaptığımız bölme işlemine benzer bir yöntemle yapılır. Uzun bölme yöntemi kullanılarak gerçekleştirilir.
Örnek:
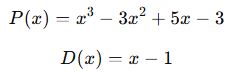
Adım adım bölme işlemi:
-
Bölünen polinomun en büyük dereceli terimi, bölenin en büyük dereceli terimine bölünür:

-
Bulunan terim, bölen polinomla çarpılır ve çıkarılır:
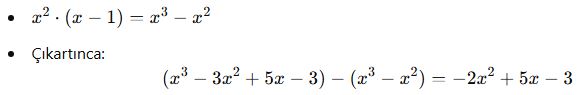
-
Yeni en büyük terim tekrar bölünür:
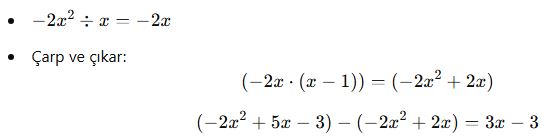
-
Son terimi bölme:
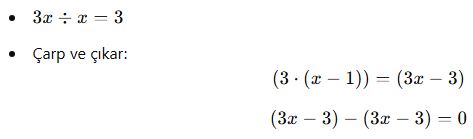
Bölüm:
![]()
Kalan:
![]()
Sonuç:
![]()
Bu durumda polinom tam bölünmüştür.
4. Polinomlarda Bölünebilme Kuralları
Bir polinomun başka bir polinoma bölünebilmesi için kalan 0 olmalıdır. Bazı özel kurallar şunlardır:
-
Bir polinom, x – a ile tam bölünüyorsa, P(a) = 0 olmalıdır.
Örnek :
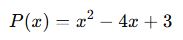
Eğer bu polinom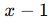 ile tam bölünebiliyorsa, P(1) = 0 olmalıdır.
ile tam bölünebiliyorsa, P(1) = 0 olmalıdır.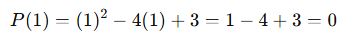
Tam bölünüyor! -
Bölme işlemi yapmadan bir polinomun başka bir polinoma tam bölünüp bölünmediğini anlamak için çarpanlara ayırma yöntemi kullanılabilir.
Örnek:
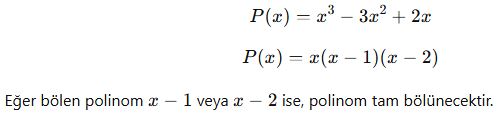
Polinomlarda Çarpanlara Ayırma Teknikleri
Polinomları çarpanlarına ayırmak, polinomu daha basit ifadelerin çarpımı şeklinde yazma işlemidir. Bu işlem, polinomların köklerini bulmada, bölünebilme testlerinde ve denklem çözümünde oldukça önemlidir. Şimdi en yaygın kullanılan çarpanlara ayırma tekniklerini inceleyelim.
1. Ortak Çarpan Parantezine Alma
Bir polinomun her teriminde ortak olan bir çarpan varsa, bu çarpanı parantez dışına alarak çarpanlara ayırabiliriz.
Örnek 1:
![]()
Her iki terimde de 3x² ortak çarpandır:
![]()
Örnek 2:
![]()
Burada ![]() ve 2 ortak çarpanlar olarak gruplanabilir:
ve 2 ortak çarpanlar olarak gruplanabilir:
![]()
Şimdi (x – 1) ortak çarpanını alalım:
![]()
2. İki Kare Farkı (Açılımı ve Tersine Kullanımı)
İki kare farkı şu formülle çarpanlara ayrılabilir:
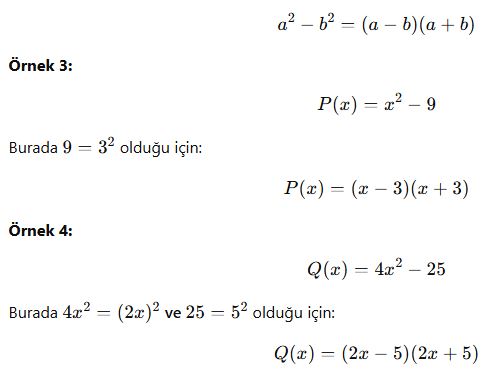
3. Tam Kare Açılımı ve Çarpanlara Ayırma
Bir ifadenin tam kare olup olmadığını kontrol etmek ve ona göre çarpanlara ayırmak önemlidir.
Tam kare ifadeler:
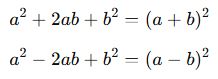
Örnek 5:
![]()
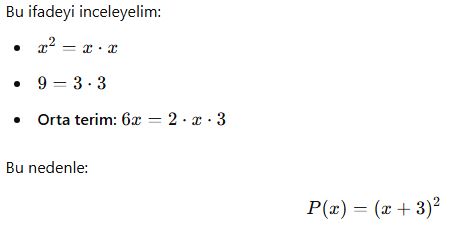

4. Çarpanlara Ayırma (İkili Gruplama Yöntemi)
Bazı polinomlar, terimleri gruplandırarak çarpanlarına ayrılabilir.

5. Çarpanları Bulma (Denklem Kökleri ile Ayırma)
Bir polinomun köklerini bulup çarpanlarına ayırabiliriz. Kökleri bulmak için polinomu sıfıra eşitleyerek çözebiliriz.
Örnek 8:
![]()
Bunu çarpanlarına ayırmak için çarpımları 6, toplamları -5 olan iki sayı arıyoruz:
![]()
Bu durumda çarpanlara ayrılmış hali:
![]()

Polinomlarda Kök Bulma ve Eşitlikler
Polinomların köklerini bulmak, onları çarpanlarına ayırmada ve denklemleri çözmede önemli bir adımdır. Bir polinomun kökü, o polinomu sıfır yapan değişken değerleridir. Bu kökler, polinom eşitliklerini çözerek bulunur. Şimdi kök bulma yöntemlerini ve polinom eşitliklerini detaylıca inceleyelim.
1. Polinomun Kökü ve Kök Bulma Yöntemleri
Bir polinomun kökü, P(a) = 0 olacak şekilde x = a değerleridir. Kökleri bulmanın birkaç yöntemi vardır:
a) Çarpanlara Ayırma Yöntemiyle Kök Bulma
Eğer polinom çarpanlarına ayrılabiliyorsa, her bir çarpan sıfıra eşitlenerek kökler bulunur.


b) Polinomun Bir Kökünü Bulup Horner Yöntemiyle Bölme
Bazı durumlarda polinom çarpanlarına kolay ayrılamayabilir. Bu gibi durumlarda bir kök bulunarak polinom bölme işlemi yapılır.
Örnek 3:
![]()
Öncelikle kök olup olmadığını kontrol edelim. P(1), P(2) veya P(3) deneyelim:
![]()
Demek ki x = 1 bir köktür. Şimdi bu kökle bölme yaparak polinomu ikinci dereceye düşürelim:
Uzun bölme veya Horner Yöntemi ile:
![]()
Sonuç:
![]()
Bunu çarpanlarına ayırırsak:
![]()
Bu durumda kökler:
![]()
2. Polinomlarda Eşitlikler
Polinomlar arasında eşitlik kurulduğunda, bilinmeyen katsayıları bulmak için bilinmeyen değerleri yerine koyarak eşitliği çözeriz.
a) Katsayı Karşılaştırma Yöntemi
Eğer iki polinom eşitse, karşılıklı aynı dereceden terimlerin katsayıları birbirine eşit olmalıdır.
Örnek 4:
Aşağıdaki polinomlar eşit olduğuna göre, a ve b değerlerini bulun:
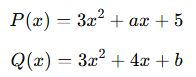

b) Belirli Bir Noktadan Geçen Polinomu Bulma
Bir polinomun belirli bir noktadan geçmesi, o noktada P(x) = 0 veya P(x) = verilen değer olmasını gerektirir.
Örnek 5:
![]()
Verilen bilgiler:
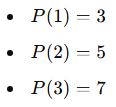
Bu değerler yerine konularak bir denklem sistemi oluşturulur:

Bu sistem çözülerek a,b,c değerleri bulunur.
Polinomlarla İlgili Çıkmış Sorular ve Çözümleri
TYT sınavında polinomlarla ilgili sorular genellikle çarpanlara ayırma, kök bulma, bölme işlemi ve katsayı ilişkileri konularını kapsar. Şimdi geçmiş yıllarda benzer tarzda çıkmış sorulara ve çözümlerine bakalım.






Polinomlar Konu Testi Çözümleri
Aşağıdaki test soruları, polinomlarla ilgili temel kavramları, işlemleri ve problem çözme becerilerini ölçmek için hazırlanmıştır.
1. Polinomun Derecesi
Soru 1:
![]()
polinomunun derecesi kaçtır?
A) 3
B) 4
C) 5
D) 6
✅ Çözüm:
Bir polinomun derecesi, en büyük üslü terimin üssüne eşittir.
Burada en büyük üs 5 olduğuna göre, derece 5’tir.
Cevap: C) 5
2. Polinomlarda Toplama İşlemi
Soru 2:
![]()
polinomlarının toplamı nedir?
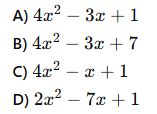
✅ Çözüm:
Polinomlar toplanırken benzer terimler toplanır:
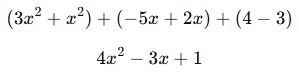
![]()
3. Polinomların Kökleri
Soru 3:

4. Polinom Çarpanlara Ayırma
Soru 4:

5. Polinom Bölme İşlemi
Soru 5:

6. Polinom Katsayıları
Soru 6:


7. Polinomun Sabit Terimi
Soru 7:
![]()
polinomunun sabit terimi kaçtır?
A) -6
B) 6
C) -7
D) 7
✅ Çözüm:
Sabit terim, x yerine 0 konularak bulunur:
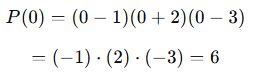
Cevap: B) 6
8. Polinom Kök Bulma
Soru 8:
![]()
polinomunun kökleri kaçtır?
A) 2 ve 4
B) 4 ve 4
C) 6 ve 2
D) 8 ve 1
✅ Çözüm:
Çarpanlara ayıralım:
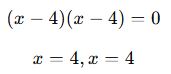
Cevap: B) 4 ve 4
9. Polinomlarla Bölünebilme
Soru 9:

