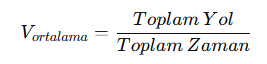İçindekiler
TYT Matematik Problemler Konu Anlatımı
Matematik problemleri, sayısal düşünme becerilerini geliştiren ve günlük hayattaki olayları matematiksel ifadelerle modellemeyi sağlayan en önemli konulardan biridir. TYT sınavında mantık yürütme, analiz yapma ve problem çözme becerilerini test eden bu sorular, pratik yapıldıkça hız kazanılan ve temel matematik kurallarını içeren bir konudur.
Problemler, öğrencinin verilen bilgileri doğru yorumlamasını, eksik veya gizli bilgileri keşfetmesini ve farklı çözüm yolları geliştirerek sonuca ulaşmasını gerektirir. Dolayısıyla, problemleri çözebilmek için yalnızca matematik bilgisi yeterli değildir; aynı zamanda mantıksal düşünme, dikkatli okuma ve stratejik çözümleme gereklidir.
Bu ünite, günlük hayatla iç içe geçmiş matematiksel olayları içerdiğinden, formülleri ezberlemek yerine problemin mantığını kavrayarak çözmek en etkili yöntem olacaktır. Her problem türünün kendine özgü çözüm stratejileri ve yaklaşımları bulunmaktadır. Şimdi, her problem türünü ayrı ayrı detaylı bir şekilde ele alarak örneklerle açıklayacağız.
Sayı Problemleri Konu Anlatımı ve Örnek Sorular
Sayı Problemleri Nedir?
Sayı problemleri, verilen sayıların belirli ilişkiler içinde olduğu ve bu ilişkileri kullanarak bilinmeyen sayıların bulunmasını gerektiren problemlerden oluşur. Matematiksel ifadeler ve denklem kurma becerisi bu tür problemlerde çok önemlidir.
Bu problemlerde genellikle:
- Bir sayının katları
- Belli sayıda artış veya azalış
- Tek ve çift sayılar
- Sayıların toplamı veya farkı gibi kavramlar kullanılır.
Sayı Problemlerini Çözerken İzlenecek Adımlar
- Verilenleri dikkatlice okuyun. Sayı ile ilgili verilen tüm bilgileri belirleyin.
- Bilinmeyenleri belirleyin. Eğer sayı bilinmiyorsa genellikle x gibi bir değişkenle ifade edilir.
- Matematiksel denklemler oluşturun. Sorunun içinde geçen ifadeleri matematiksel olarak yazın.
- Denklemi çözerek bilinmeyeni bulun. Denklem çözüldüğünde sayının değeri ortaya çıkacaktır.
- Sonucu kontrol edin. Sorunun koşullarına uygun olup olmadığını mutlaka kontrol edin.
Sayı Problemlerine Örnekler
Örnek 1: Bir Sayının Belirlenmesi
Bir sayının 3 katının 4 fazlası, aynı sayının 2 katının 7 fazlasına eşittir. Bu sayı kaçtır?
Çözüm:
- Sayıyı x olarak belirleyelim.
- Verilen ifadeye göre denklemimizi yazalım:

Örnek 2: Ardışık Sayılar Problemi
Üç ardışık tek sayının toplamı 45’tir. Bu sayıların en küçüğü kaçtır?
Çözüm:
- Ardışık tek sayıları x, x+2, x+4 olarak ifade edebiliriz.
- Verilen bilgiye göre denklemimizi yazalım:
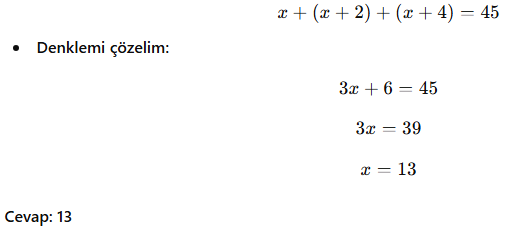
Örnek 3: Sayıların Toplamı Problemi
İki sayının toplamı 36’dır. Birinci sayı, ikinci sayının 2 katından 4 fazladır. Büyük sayı kaçtır?
Çözüm:
- Küçük sayıyı x olarak belirleyelim.
- Büyük sayı 2x + 4 olarak ifade edilir.
- Verilen bilgiye göre denklemimizi yazalım:

Örnek 4: Tek ve Çift Sayılar Problemi
Bir çift sayının yarısının 3 eksiği, o sayının 5 fazlasına eşittir. Bu sayı kaçtır?
Çözüm:
- Çift sayıyı x olarak belirleyelim.
- Denklemimizi yazalım:

Sayı Problemlerinde Dikkat Edilmesi Gerekenler
✅ Sorunun içeriğini iyi analiz edin. Sayılarla ilgili verilen bilgileri dikkatlice okuyun.
✅ Bilinmeyenleri doğru belirleyin. Sayıyı genellikle x olarak ifade edin ve denklem oluşturun.
✅ İşlemleri dikkatli yapın. Denklem kurarken yanlışlık yapmamaya özen gösterin.
✅ Sonucu kontrol edin. Bulduğunuz sayı, sorunun tüm koşullarını sağlıyor mu? Kontrol etmeyi unutmayın.
Özet
- Sayı problemleri denklem kurmayı gerektiren problemlerdir.
- Ardışık sayılar, çift ve tek sayılar, toplam ve fark ilişkileri sıkça sorulur.
- Denklem kurarak ve bilinmeyeni tanımlayarak sorular kolayca çözülebilir.
Kesir Problemleri Konu Anlatımı ve Örnek Sorular
Kesir Problemleri Nedir?
Kesir problemleri, belirli bir miktarın kesirli (parçalı) ifadesiyle ilişkili olan problemlerdir. Bu tür sorular, günlük hayatta dilimleme, bölme, oran ve paylaşım konularında sıkça karşımıza çıkar.
Özellikle “bir sayının yarısı, üçte biri, dörtte biri” gibi ifadeleri anlamak ve matematiksel bir denklem kurmak kesir problemlerinin temelidir.
Kesir Problemlerini Çözerken İzlenecek Adımlar
- Problemi dikkatlice okuyun ve kesir ifadelerini belirleyin.
- Bilinmeyeni “x” ile tanımlayın (Eğer toplam bilinmiyorsa tüm miktarı x olarak ifade edin).
- Matematiksel ifadeleri denklem hâline getirin.
- Denklemi çözüp bilinmeyeni bulun.
- Sonucu kontrol edin. Sorunun tüm şartlarını sağladığından emin olun.
Kesir Problemlerine Örnekler
Örnek 1: Bir Sayının Belirli Bir Kesri
Bir sayının üçte biri 12’dir. Bu sayı kaçtır?
Çözüm:
- Sayıyı x olarak belirleyelim.
- Üçte biri verilmiş olduğuna göre:
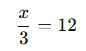
- Denklemi çözelim:
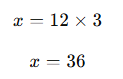
Cevap: 36
Örnek 2: Bir Sayının Kesirleri Toplamı
Bir sayının yarısı ile dörtte biri toplamı 30’dur. Bu sayı kaçtır?
Çözüm:
- Sayıyı x olarak belirleyelim.
- Verilen ifadeye göre denklemimizi yazalım

Örnek 3: Bir Sayının Kesirleri Arasındaki İlişki
Bir sayının beşte ikisi, üçte birine eşittir. Bu sayı kaçtır?
Çözüm:
- Sayıyı x olarak belirleyelim.
- Verilen eşitliği matematiksel olarak yazalım:
![]()

Örnek 4: Bir Sayının Kesirli Artış ve Azalışı
Bir sayının üçte biri 5 artırıldığında, sayının yarısına eşit oluyor. Bu sayı kaçtır?
Çözüm:
- Sayıyı x olarak belirleyelim.
- Verilen ifadeye göre denklemimizi yazalım:
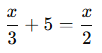
- Denklemi düzenleyelim:
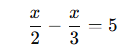
- Ortak payda bulalım (6):
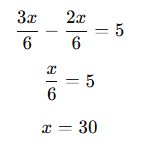
Cevap: 30
Örnek 5: Kesirlerle Paylaşım Problemi
Bir sınıftaki öğrencilerin dörtte biri futbol oynuyor, geri kalan 18 öğrenci ise basketbol oynuyor. Sınıfta toplam kaç öğrenci vardır?
Çözüm:

Kesir Problemlerinde Dikkat Edilmesi Gerekenler
✅ Verilen kesirleri doğru anlayın. Problemin tanımında geçen yarısı, üçte biri, dörtte biri gibi ifadeleri doğru matematiksel modele dönüştürün.
✅ Bilinmeyeni doğru tanımlayın. Çoğu kesir problemi bir bilinmeyene dayalı olduğu için, x gibi değişkenler kullanın.
✅ Kesirleri toplarken veya çıkartırken ortak payda kullanın. Kesirlerin paydaları farklıysa eşitleme işlemi yapmayı unutmayın.
✅ Sonucu kontrol edin. Bulduğunuz sayının verilen kesirlerle sağladığı eşitliği kontrol edin.
Özet
- Kesir problemleri, verilen sayılarla ilgili “yarısı”, “üçte biri”, “beşte ikisi” gibi ifadeleri içerir.
- Kesirli ifadeleri denkleme dönüştürmek en önemli adımdır.
- Ortak payda kullanarak işlemleri düzenlemek çözümü kolaylaştırır.
- Problemi dikkatlice okuyarak matematiksel modeli oluşturun ve denklemi çözün.
Yaş Problemleri Konu Anlatımı ve Örnek Sorular
Yaş Problemleri Nedir?
Yaş problemleri, kişilerin veya nesnelerin yaşları arasındaki ilişkileri kullanarak bilinmeyen yaşları bulmayı gerektiren matematiksel problemlerden oluşur. Bu tür problemler, genellikle geçmiş, şimdi ve gelecek gibi farklı zaman dilimlerine göre şekillenir.
Yaş problemlerinin temel mantığı, kişilerin yaşlarının zamanla değişmesi fakat aralarındaki yaş farkının değişmemesidir. Yani iki kişi arasındaki yaş farkı her zaman sabit kalır.
Yaş Problemlerinde Kullanılan Temel Stratejiler
- Bilinmeyeni belirleyin.
- Kişinin veya kişilerin yaşını x gibi bir değişkenle ifade edin.
- Zaman değişimini takip edin.
- Şu anki yaşlarını x olarak yazdıysanız, geçmişte (x – t), gelecekte (x + t) olarak ifade edilir.
- Yaş farkını unutmayın.
- İki kişi arasındaki yaş farkı her zaman sabittir.
- Denklem kurup çözümleyin.
Yaş Problemlerine Örnekler
Örnek 1: Yaş Farkı Değişmez
Ahmet ve Mehmet’in yaşları toplamı 40’tır. 4 yıl önce Ahmet’in yaşı Mehmet’in yaşının 2 katıydı. Ahmet’in şimdiki yaşı kaçtır?
Çözüm:


Örnek 2: Geçmişte ve Şu Anki Yaşlar
Bir babanın yaşı, oğlunun yaşının 4 katıdır. 10 yıl sonra babanın yaşı, oğlunun yaşının 2 katı olacak. Babanın şimdiki yaşı kaçtır?
Çözüm:


Örnek 3: Gelecekteki Yaşlar
Bir anne ile kızının yaşları toplamı 50’dir. 5 yıl sonra annenin yaşı, kızının yaşının 3 katı olacak. Annenin şimdiki yaşı kaçtır?
Çözüm:
- Annenin yaşını x, kızının yaşını y olarak belirleyelim.
- Şu anki yaşları için denklem:


Yaş Problemlerinde Dikkat Edilmesi Gerekenler
✅ Yaş farkı her zaman sabittir. İki kişinin arasındaki yaş farkı zamanla değişmez.
✅ “Önce” ve “sonra” ifadelerine dikkat edin. Geçmiş ve gelecekteki yaş ifadelerini doğru formüle edin.
✅ Problemi matematiksel modele dönüştürün. Yaş ifadelerini denklem hâline getirmek çözümü kolaylaştırır.
✅ Bilinmeyeni belirleyin. Eğer kişi sayısı fazlaysa, yaşları x, y, z… gibi değişkenlerle ifade edin.
✅ Çözümü kontrol edin. Bulduğunuz yaşları sorunun koşullarına uygun mu diye kontrol etmeyi unutmayın.
Özet
- Yaş problemleri, farklı zaman dilimlerinde kişilerin yaşları arasındaki ilişkileri içeren problemlerdir.
- Zaman ilerledikçe yaş artar fakat yaş farkı sabit kalır.
- Geçmiş ve gelecekteki yaşlara dikkat ederek denklemler kurulur.
- Bilinmeyenleri tanımlayıp denklemi çözüp sonucu kontrol etmek gerekir.
Hareket ve Hız Problemleri Konu Anlatımı ve Örnek Sorular
Hareket ve Hız Problemleri Nedir?
Hareket problemleri, bir cismin belirli bir hızla belirli bir süre boyunca hareket etmesi sonucunda aldığı yolu bulma ile ilgilidir. TYT’de sıkça karşılaşılan bu problem türü, hız, zaman ve yol arasındaki ilişkilere dayalıdır.
Hareket problemlerinde temel formül:
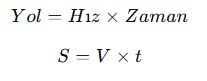
Burada:
- S → Alınan yol (km, m vb. birimlerde ölçülür),
- V → Hız (km/s, m/s vb. birimlerde ölçülür),
- t → Zaman (saat, dakika vb. birimlerde ölçülür).
Hareket Problemlerinde Kullanılan Temel Stratejiler
- Birimleri aynı hale getirin. Km/saat ile dakika kullanılıyorsa, birimleri uygun hale getirin.
- Formülü belirleyin: Yol, hız veya zamanı bulmanız gerekiyorsa formülü doğru şekilde kullanın.
- Hareket yönlerini dikkate alın. Karşılıklı hareket, aynı yönde hareket gibi durumları inceleyin.
- Denklemi oluşturun ve çözün.
Hareket Problemlerinin Çeşitleri
- Tek Hareketli Problemler
- İki Hareketlinin Karşılıklı Hareketi
- İki Hareketlinin Aynı Yönde Hareketi
- Geri Dönüş Problemleri
- Hareketli Nesneler Arasındaki Ortalama Hız
1. Tek Hareketli Problemler
Örnek 1: Bir araç saatte 60 km hızla 4 saat boyunca hareket ederse kaç km yol alır?
Çözüm:
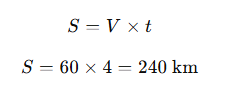
Cevap: 240 km
2. İki Hareketlinin Karşılıklı Hareketi
İki araç karşılıklı hareket ediyorsa toplam hızları toplanır:
Örnek 2: İki şehir arası 300 km’dir. Biri saatte 50 km, diğeri saatte 70 km hızla birbirine doğru hareket eden iki araç kaç saat sonra karşılaşır?
Çözüm:
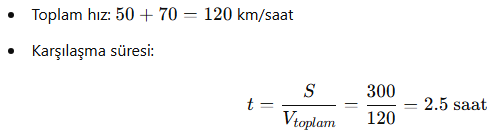
Cevap: 2.5 saat
3. İki Hareketlinin Aynı Yönde Hareketi
İki araç aynı yönde hareket ediyorsa, aradaki mesafe kapanma süresi ile bulunur:
![]()
Örnek 3: 100 km mesafeyle hareket eden iki araçtan biri 80 km/s, diğeri 60 km/s hızla ilerliyor. Daha hızlı olan araç, diğerine kaç saat sonra yetişir?
Çözüm:
- Hız farkı:
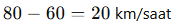
- Yaklaşma süresi:
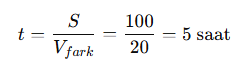
Cevap: 5 saat
4. Geri Dönüş Problemleri
Biri gidip geri dönerken, diğeri sabit kalırsa aynı yolu iki kez aldığı unutulmamalıdır.
Örnek 4: Ali, 40 km hızla bir noktaya gidiyor, dönüşte 60 km hızla dönüyor. Yolculuk toplam 5 saat sürdüğüne göre, gittiği mesafe kaç km’dir?
Çözüm:
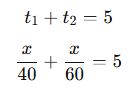
Ortak payda ile çözelim:
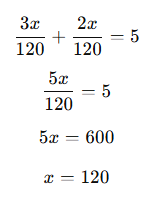
Cevap: 120 km
5. Ortalama Hız Problemleri
Ortalama hız, toplam yolun toplam zamana bölünmesiyle bulunur.
Örnek 5: Bir araç, yolun ilk yarısını 40 km/s, ikinci yarısını 60 km/s ile gidiyor. Yolun tamamındaki ortalama hızı kaçtır?

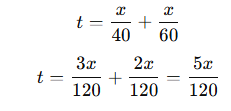
Ortalama hız:
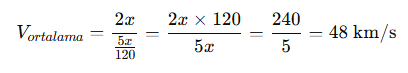
Cevap: 48 km/s
Hareket Problemlerinde Dikkat Edilmesi Gerekenler
✅ Birimlere dikkat edin. Dakika ve saat gibi farklı zaman birimleri varsa dönüştürme yapın.
✅ Karşılıklı harekette hızları toplayın. Birbirine yaklaşma hızını ![]() olarak belirleyin.
olarak belirleyin.
✅ Aynı yönde harekette hız farkını kullanın. Daha hızlı olan aracın diğerine yetişme süresini bulmak için ![]() hesaplayın.
hesaplayın.
✅ Ortalama hız hesaplamalarında doğru yöntemi kullanın. Farklı hızlarla gidilen mesafelerde ortalama hız aritmetik ortalama değildir, formüle göre hesaplanmalıdır.
Özet
- Hareket problemleri, hız, zaman ve yol ilişkisine dayanır.
- Formül:
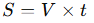
- Karşılıklı hareket: Hızlar toplanır.
- Aynı yönde hareket: Hız farkı kullanılır.
- Geri dönüş problemlerinde toplam yol ve toplam zaman dikkate alınır.
- Ortalama hız, toplam yolun toplam zamana bölünmesiyle bulunur.
İşçi ve Emek Problemleri Konu Anlatımı ve Örnek Sorular
İşçi ve Emek Problemleri Nedir?
İşçi ve emek problemleri, bir işin belirli bir sürede tamamlanmasıyla ilgili hesaplamaları içeren matematiksel problemlerden oluşur. Bu tür sorular, işin tamamlanma süresi, işçi sayısı ve çalışma hızları arasındaki ilişkilere dayanır.
Bu problemlerde temel olarak şu prensipler kullanılır:
- Bir işçi bir işi xx saatte yapıyorsa, işçinin 1 saatte yaptığı iş miktarı
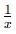 olur.
olur. - Birden fazla işçi aynı anda çalışıyorsa, bireysel iş hızları toplanarak toplam hız bulunur.
- Daha fazla işçi aynı işi yaparsa, tamamlanma süresi kısalır (ters orantı).
İşçi ve Emek Problemlerinde Kullanılan Temel Formüller
- Bir işçi bir işi xx günde yapıyorsa, bir günde yaptığı iş miktarı:
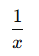
- nn işçi birlikte çalışıyorsa, bir günde yapılan iş miktarı:
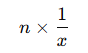
- İşin tamamlanma süresi:
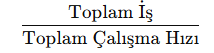
- İşçi sayısı arttıkça, işin tamamlanma süresi azalır. İşçi sayısı azaldıkça işin tamamlanma süresi artar.
İşçi ve Emek Problemlerine Örnekler
Örnek 1: Tek İşçi Problemi
Bir işçi bir işi 12 günde bitirebiliyorsa, bu işçi 1 günde işin kaçta kaçını yapar?
Çözüm:
- İşçinin 1 günde yaptığı iş miktarı:
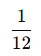
Cevap: ![]() (İşin 1/12’sini yapar.)
(İşin 1/12’sini yapar.)
Örnek 2: Birlikte Çalışma Problemi
Ali bir işi 6 günde, Veli aynı işi 9 günde bitiriyor. İkisi birlikte çalışırsa işi kaç günde bitirirler?
Çözüm:

Örnek 3: İşçi Sayısı Artarsa İşin Süresi Kısalır
10 işçi bir işi 12 günde bitirebiliyorsa, aynı işi 15 işçi kaç günde bitirir?
Çözüm:
- Toplam iş miktarı sabittir. İşçi sayısı arttıkça süre azalır.
- İşçi ve süre ters orantılıdır:
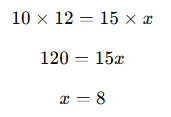
Cevap: 8 gün
Örnek 4: Eksilen İşçi Problemi
20 işçi bir işi 15 günde bitirebiliyor. 5 işçi işten ayrılırsa, geri kalan işçiler aynı işi kaç günde bitirir?
Çözüm:
- İşçi ve süre ters orantılıdır.
- İlk durumda:
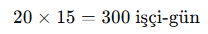
- Yeni durumda:
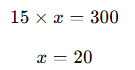
Cevap: 20 gün
Örnek 5: Değişen Hızlarla Çalışma Problemi
Bir işçi bir işi 20 günde, başka bir işçi 30 günde bitirebiliyor. İlk işçi 5 gün yalnız çalıştıktan sonra, ikinci işçi de katılıyor. İş ne kadar sürede tamamlanır?
Çözüm:



İşçi ve Emek Problemlerinde Dikkat Edilmesi Gerekenler
✅ İşçi sayısı ve süre ters orantılıdır. İşçi sayısı arttıkça iş süresi azalır, işçi sayısı azaldıkça iş süresi artar.
✅ Bir işçinin 1 günde yaptığı iş miktarını hesaplayın. Her zaman “iş bölü gün” şeklinde düşünün.
✅ Birlikte çalışan işçilerin hızlarını toplayın. Eğer birden fazla kişi çalışıyorsa, bireysel hızlarını toplayarak toplam hızı hesaplayın.
✅ İlk başta tek başına çalışıp sonra yardım alan işçileri hesaplayın. Önce yalnız çalışanın ne kadar iş yaptığını bulun, sonra birlikte çalışma süresini hesaplayın.
Özet
- İşçi sayısı arttıkça iş süresi kısalır (ters orantı).
- Bir işçinin 1 günde yaptığı iş
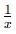 olarak ifade edilir.
olarak ifade edilir. - Birden fazla işçi varsa hızları toplanarak süre hesaplanır.
- İlk başta tek başına çalışan bir işçi varsa, yaptığı iş miktarı hesaplanarak kalan iş belirlenir.
Yüzde Problemleri Konu Anlatımı ve Örnek Sorular
Yüzde Problemleri Nedir?
Yüzde problemleri, bir miktarın belirli bir yüzdesinin hesaplanması veya bir miktarın yüzde cinsinden değişiminin bulunması ile ilgili problemlerdir. Günlük hayatta indirimler, faiz hesaplamaları, kâr-zarar oranları, vergi hesaplamaları gibi birçok alanda karşımıza çıkar.
Yüzde hesaplamalarında en temel formül şudur:
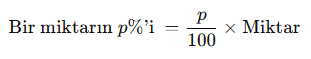
Yüzde Problemlerinde Kullanılan Temel Stratejiler
- Yüzdeyi ondalık veya kesir formuna çevirin.
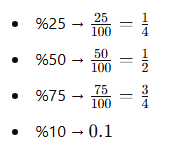
- Arttırma ve azaltma işlemlerinde başlangıç değerine göre yüzde hesaplayın.
- Bileşik yüzde değişimlerinde sırayla işlemi uygulayın.
- İndirim veya kâr hesaplamalarında önce değişimi, sonra nihai sonucu bulun.
Yüzde Problemlerine Örnekler
Örnek 1: Bir Sayının Yüzdesini Bulma
Bir ürünün fiyatı 240 TL’dir. Bu ürünün %20’si kaç TL’dir?
Çözüm:
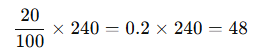
Cevap: 48 TL
Örnek 2: Bir Sayının Belirli Bir Yüzdesi Verildiğinde Tam Değeri Bulma
Bir öğrencinin matematik sınavından aldığı puan, toplam puanın %40’ıdır ve 28 puandır. Sınavın toplam puanı kaçtır?
Çözüm:
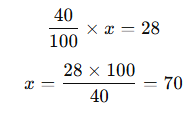
Cevap: 70 puan
Örnek 3: Yüzde Arttırma ve Azaltma
Bir ürünün fiyatı 300 TL’dir. Fiyat önce %25 artırılıp sonra %10 azaltılırsa yeni fiyat kaç TL olur?
Çözüm:
- %25 artış:
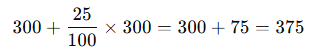
- %10 azalış:
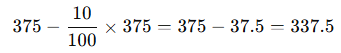
Cevap: 337.5 TL
Örnek 4: Bileşik Yüzde Problemi
Bir ürünün fiyatı %20 artırılıp sonra %20 azaltılırsa, fiyat başlangıçtaki değere döner mi?
Çözüm:
- İlk artış:
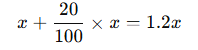
- İkinci azalış:
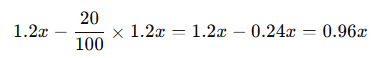
Ürün fiyatı başlangıç değerinin %96’sına düşer. Tam olarak geri dönmez.
Örnek 5: İndirimli Fiyat Hesaplama
Bir mağazada %30 indirim uygulanıyor. 500 TL’lik bir ürünün indirimli fiyatı kaç TL olur?
Çözüm:
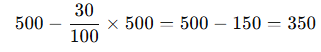
Cevap: 350 TL
Örnek 6: Yüzde Değişimi Bulma
Bir ürünün fiyatı 200 TL’den 250 TL’ye yükselmiştir. Yüzde kaç artış olmuştur?
Çözüm:
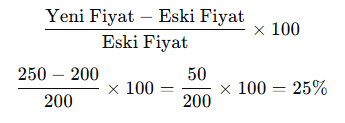
Cevap: %25 artış
Örnek 7: Bir Oranın Yüzde Karşılığı
Bir sınavda 40 sorunun 28’ini doğru yapan bir öğrenci, kaç puan almıştır? (100 puan üzerinden)
Çözüm:
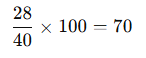
Cevap: 70 puan
Yüzde Problemlerinde Dikkat Edilmesi Gerekenler
✅ Yüzdeyi kesir veya ondalık sayıya çevirerek işlemi kolaylaştırın.
✅ Artış ve azalış işlemlerinde yüzdeyi tek tek uygulayın. Birden fazla işlem varsa sırayla hesaplayın.
✅ Bileşik yüzdelerde doğrudan toplayıp çıkarmak yanlış olur. Önce artışı, sonra azalışı uygulayın.
✅ İndirimli fiyatları hesaplarken önce indirimi bulup sonra çıkarın.
✅ Yüzde değişim sorularında farkı, başlangıç değerine bölerek yüzdelik değişimi bulun.
Özet
- Yüzde hesaplamaları günlük hayatta geniş bir kullanım alanına sahiptir.
- Bir sayının yüzdesini bulmak için
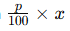 formülü kullanılır.
formülü kullanılır. - Artış ve azalış hesaplamalarında önce artışı, sonra azalışı hesaplamak gerekir.
- Bileşik yüzdeler doğrudan toplanmaz, sırayla uygulanır.
- İndirim ve kâr zarar hesaplarında önce fark bulunur, sonra toplamdan çıkarılır veya eklenir.
Kâr-Zarar Problemleri Konu Anlatımı ve Örnek Sorular
Kâr-Zarar Problemleri Nedir?
Kâr ve zarar problemleri, bir malın alış ve satış fiyatları arasındaki farkın kâr mı yoksa zarar mı olduğunu bulmaya dayalıdır. Ticaret, ekonomi ve finans alanlarında çok önemli bir konudur.
Bu tür problemler genellikle şu terimleri içerir:
- Alış fiyatı (A) → Bir malın satın alındığı fiyat.
- Satış fiyatı (S) → Bir malın satıldığı fiyat.
- Kâr veya zarar miktarı → Alış ve satış fiyatı arasındaki fark.
- Kâr veya zarar yüzdesi → Kâr veya zararın alış fiyatına göre yüzdesi.
Kâr-Zarar Problemlerinde Kullanılan Temel Formüller
- Kâr veya Zarar Miktarı:
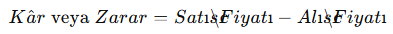
- Kâr Yüzdesi:
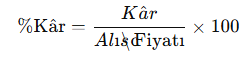
- Zarar Yüzdesi:
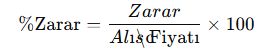
- Satış fiyatı bulma:
- Eğer kâr edilmişse:
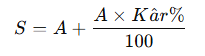
- Eğer zarar edilmişse:
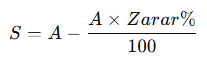
- Eğer kâr edilmişse:
- Bileşik kâr veya zarar (Birden fazla kez artış veya azalış olduğunda):
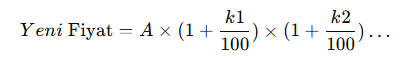
Kâr-Zarar Problemlerine Örnekler
Örnek 1: Kâr Hesaplama
Bir tüccar 500 TL’ye aldığı bir malı 650 TL’ye satıyor. Bu işlemde kâr yüzdesi kaçtır?
Çözüm:
- Kâr miktarı:
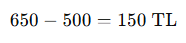
- Kâr yüzdesi:
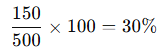
Cevap: %30 kâr
Örnek 2: Zarar Hesaplama
Bir kişi 400 TL’ye aldığı bir telefonu 350 TL’ye satmıştır. Zarar yüzdesi kaçtır?
Çözüm:
- Zarar miktarı:
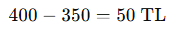
- Zarar yüzdesi:
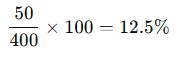
Cevap: %12.5 zarar
Örnek 3: Satış Fiyatı Bulma
Bir tüccar, %25 kâr etmek istediği bir ürünü 240 TL’ye almıştır. Satış fiyatı ne olmalıdır?
Çözüm:
- Satış fiyatı formülü:
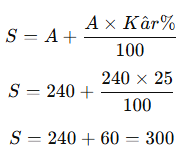
Cevap: 300 TL
Örnek 4: Bileşik Kâr Problemi
Bir tüccar, bir ürünü önce %20, sonra %10 kârla satarsa, toplam kâr yüzdesi kaç olur?
Çözüm:
Bileşik kâr hesaplamasında, artışları tek tek çarpan olarak alırız:
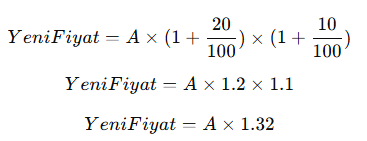
Sonuç olarak, %32 kâr elde edilir.
Cevap: %32 kâr
Örnek 5: Bileşik Zarar Problemi
Bir ürün önce %10 zararına, sonra %15 zararına satılıyor. Toplam zarar yüzdesi kaçtır?
Çözüm:
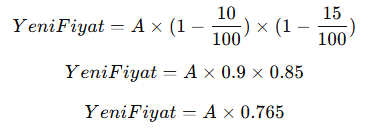
Sonuç olarak, %23.5 zarar elde edilir.
Cevap: %23.5 zarar
Örnek 6: Bir Malın Alış Fiyatını Bulma
Bir ürün %20 kârla 480 TL’ye satılıyorsa, bu ürünün alış fiyatı kaç TL’dir?
Çözüm:
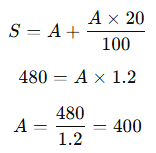
Cevap: 400 TL
Örnek 7: Kâr ve Zarar Karışık Problem
Bir malın alış fiyatı 600 TL’dir. Ürün önce %30 kârla, sonra %20 zararla satılıyor. Son satış fiyatı kaç TL olur?
Çözüm:
- %30 kâr ekleyelim:
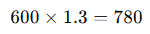
- %20 zarar hesaplayalım:

Cevap: 624 TL
Kâr-Zarar Problemlerinde Dikkat Edilmesi Gerekenler
✅ Kâr veya zarar yüzdesi her zaman alış fiyatı üzerinden hesaplanır.
✅ Satış fiyatını bulurken artış veya azalış işlemlerini sırasıyla yapın.
✅ Bileşik kâr veya zarar durumlarında çarpma işlemi kullanın.
✅ Kâr ve zarar arka arkaya uygulanıyorsa doğrudan toplanmaz, yüzde değişimi ayrı ayrı hesaplanır.
✅ İndirimli fiyatlarla ilgili sorularda, önce indirimi hesaplayıp fiyatı çıkartın.
Özet
- Kâr veya zarar miktarı, satış ve alış fiyatlarının farkıdır.
- Kâr ve zarar yüzdesi alış fiyatına göre hesaplanır.
- Bileşik kâr ve zarar hesaplamalarında sırasıyla işlemleri yapmalısınız.
- Kâr ve zarar yüzdeleri doğrudan toplanmaz, çarpan yöntemiyle hesaplanır.
Karışım Problemleri Konu Anlatımı ve Örnek Sorular
Karışım Problemleri Nedir?
Karışım problemleri, farklı bileşenlerin belirli oranlarda karıştırılmasıyla elde edilen yeni karışımların bileşimini ve yüzdesel oranlarını hesaplamaya yönelik problemlerdir.
Bu tür problemler genellikle:
- İki veya daha fazla madde karıştırıldığında, yeni karışımın bileşenlerini bulma
- Belirli bir oranda saf madde ekleme veya çıkarma
- Farklı oranlardaki karışımları karıştırarak yeni karışım oluşturma gibi konuları içerir.
Karışım Problemlerinde Kullanılan Temel Formüller
- Karışımın Toplam Miktarı:


Karışım Problemlerine Örnekler
Örnek 1: Karışımın Yüzde Hesabı
30 litrelik bir tuzlu su çözeltisinin %20’si tuz ise, çözeltide kaç litre tuz vardır?
Çözüm:
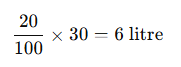
Cevap: 6 litre tuz
Örnek 2: Yeni Karışımın Yüzde Oranı
40 litre %30 tuz içeren bir çözeltiye 20 litre %50 tuz içeren başka bir çözelti ekleniyor. Yeni karışımın tuz yüzdesi kaç olur?
Çözüm:
-
Tuz miktarlarını ayrı ayrı hesaplayalım:

Örnek 3: Saf Madde Ekleme Problemi
Bir karışımdaki %30 tuz oranını %50’ye çıkarmak için kaç litre saf tuz eklenmelidir? Karışım 40 litredir.
Çözüm:

Örnek 4: Su Ekleyerek Oranı Azaltma
50 litre %40 alkol içeren bir karışıma kaç litre su eklenirse, alkol oranı %25 olur?
Çözüm:

Örnek 5: Karışımdan Madde Çıkarma
60 litre %40 tuzlu sudan, %30 oranına düşürmek için kaç litre saf su eklenmelidir?
Çözüm:

Karışım Problemlerinde Dikkat Edilmesi Gerekenler
✅ Oranları doğru hesaplayın. Tuz, alkol, şeker gibi bileşenlerin yüzdesel oranlarını dikkatlice yazın.
✅ İki karışımı birleştirirken her bileşenin ayrı ayrı miktarını bulun. Önce bileşen miktarlarını hesaplayın, sonra toplam karışımı bulun.
✅ Ekleme veya çıkarma işlemlerinde, yüzdelik denklemler kullanın. Mevcut oran üzerinden işlemi denkleme çevirin.
✅ Çıkarma işlemlerinde yüzdelik oranı tersinden düşünün. Yeni oran, azaltılan maddenin miktarına bağlı olarak değişir.
Özet
- Karışım problemleri, belirli yüzdelerdeki bileşenlerin karıştırılmasıyla yeni bileşimlerin hesaplanmasını içerir.
- Yeni oranı bulmak için bileşenlerin ayrı ayrı miktarlarını belirleyip oran formüllerini uygulamak gerekir.
- Bileşik karışımlarda sırasıyla işlemleri yaparak nihai yüzdelik değeri hesaplamak önemlidir.
- Madde ekleme veya çıkarma işlemlerinde, yüzdelik denklem kurarak çözüm sağlanır.
TYT Matematik: Problemler Ünitesi Testi
1. Sayı Problemleri
Bir sayının üçte biri, dörtte birinden 2 fazladır. Bu sayı kaçtır?
A) 24
B) 36
C) 48
D) 60
2. Kesir Problemleri
Bir öğrenci sınavdaki soruların 2/5’ini doğru yapmış ve 18 soruyu yanlış yapmıştır. Sınavda kaç soru vardı?
A) 40
B) 45
C) 50
D) 60
3. Yaş Problemleri
Bir babanın yaşı, oğlunun yaşının 4 katıdır. 12 yıl sonra babanın yaşı, oğlunun yaşının 2 katı olacak. Babanın şu anki yaşı kaçtır?
A) 32
B) 36
C) 40
D) 44
4. Hareket ve Hız Problemleri
Bir araç, saatte 60 km hızla 3 saat yol aldıktan sonra, hızını 80 km/s yaparak 2 saat daha yol alıyor. Toplamda kaç km yol almıştır?
A) 240
B) 260
C) 280
D) 300
5. İşçi ve Emek Problemleri
3 işçi bir işi 12 günde bitirebiliyorsa, aynı hızda çalışan 4 işçi bu işi kaç günde bitirir?
A) 6
B) 8
C) 9
D) 10
6. Yüzde Problemleri
Bir ürünün fiyatı önce %20 artırılmış, sonra %10 indirilmiştir. Başlangıç fiyatı 500 TL ise, son fiyatı kaç TL olur?
A) 520
B) 530
C) 540
D) 550
7. Kâr-Zarar Problemleri
Bir mal %25 kârla 375 TL’ye satılmıştır. Bu malın alış fiyatı kaç TL’dir?
A) 280
B) 300
C) 320
D) 350
8. Karışım Problemleri
40 litre %30 tuz içeren bir çözeltiye 20 litre %50 tuz içeren başka bir çözelti ekleniyor. Yeni karışımın tuz yüzdesi kaç olur?
A) %36
B) %38
C) %40
D) %42
9. İndirim ve Kâr Problemleri
Bir mağazada etiket fiyatı 250 TL olan bir ürün %30 indirimle satılmaktadır. Kasada ayrıca %10 ek indirim uygulanıyorsa, ürünün nihai satış fiyatı kaç TL olur?
A) 150
B) 157.5
C) 160
D) 165
10. Bileşik Problemler
Bir çiftçi, 100 kg buğdayın önce %20’sini satıyor, sonra kalan miktarın %25’ini kullanıyor. Geriye kaç kg buğday kalmıştır?
A) 55
B) 60
C) 65
D) 70
Cevap Anahtarı
- C
- C
- C
- D
- B
- C
- B
- A
- B
- B