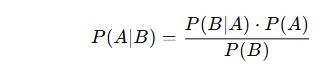Veriden Olasılığa: Olaylar Arasındaki Bağıntıyı Matematiksel Yolla Keşfetmek. Hayatın her anı belirsizliklerle doludur. Geleceği kesin olarak öngöremesek de, olayların gerçekleşme ihtimallerini matematiksel modeller yardımıyla tahmin edebiliriz. “Veriden Olasılığa” ünitesi, öğrencilere olasılık teorisinin en derin kavramlarından biri olan koşullu olasılığı öğretirken, aynı zamanda veriye dayalı çıkarım ve tahmin becerilerini geliştirmeyi amaçlar.
Bu ünitede, bir olayın meydana gelmesinin başka bir olaya bağlı olduğu durumlar incelenir. Olasılıklar yalnızca sayıların oyunu değildir; olayların birbirine bağlılığı, bağımsızlığı, ya da önceden edinilmiş bilgiler doğrultusunda yeniden değerlendirilmesi gerektiğinde işler karmaşıklaşır. İşte bu noktada Bayes Teoremi devreye girer ve bize mevcut veriler ışığında nasıl mantıklı çıkarımlar yapabileceğimizi gösterir.
10. Sınıf Matematik Veriden Olasılığa Konusu, günlük yaşamda kullanılan test sistemlerinden yapay zekâya, finans analizlerinden güvenlik protokollerine kadar birçok alanda bu ünitenin sunduğu kavramlar karşımıza çıkar. Öğrenciler bu üniteyle birlikte yalnızca sınavlara değil, gerçek dünya problemlerine de daha hazırlıklı hale gelir.
Günlük hayatta kararlar alırken olayların birbirine bağlı olması, olasılık hesaplamalarını daha karmaşık ama aynı zamanda daha anlamlı hâle getirir. “Veriden Olasılığa” ünitesinde öğrenciler, bir olayın olasılığının başka bir olayın gerçekleşip gerçekleşmemesine bağlı olarak nasıl değiştiğini öğreneceklerdir. Koşullu olasılık, bağımlı ve bağımsız olaylar ve Bayes teoremi bu ünitenin temel konularıdır.
Bu ünite sayesinde öğrenciler, bir olayın gerçekleşme ihtimalinin yalnızca kendi doğasına değil, başka olayların olup olmamasına da bağlı olabileceğini kavrayacak ve bu bilgiyi kullanarak mantıklı çıkarımlar, matematiksel modellemeler ve istatistiksel tahminler yapabileceklerdir.
İçindekiler
Koşullu Olasılık
📌 Tanım
Koşullu olasılık, bir olayın gerçekleşme olasılığının, başka bir olayın gerçekleştiği bilindiğinde nasıl değiştiğini gösterir.
Örneğin; bir torbadan önce kırmızı top çekildiği bilinmişse, ikinci topun kırmızı olma olasılığı bu bilgiye göre değişir.
Bağımlı ve Bağımsız Olaylar
-
Bağımsız olaylar:
Bir olayın gerçekleşmesi, diğerinin olasılığını etkilemez.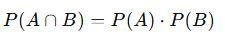
-
Bağımlı olaylar:
Bir olayın gerçekleşmesi, diğerinin olasılığını etkiler.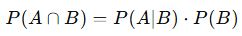
Örnek:
Bir torbada 3 kırmızı, 2 mavi top var. Rastgele bir top çekiliyor, geri konmadan ikinci bir top çekiliyor.
-
Çekilen ilk top kırmızı ise, ikinci topun kırmızı olma olasılığı nedir?
✅ Çözüm:
-
İlk kırmızı → geriye 2 kırmızı, 2 mavi kalır → toplam 4 top
-
İkinci kırmızının olasılığı:
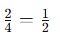
→ Koşullu olasılıktır, çünkü birinci olay sonucu ikinciyi etkiliyor.
Örnek Soru:
Bir okulda 60 öğrenci vardır. 40’ı basketbol, 30’u voleybol oynamaktadır. 20 öğrenci her iki sporu da yapmaktadır.
Basketbol oynayan bir öğrencinin voleybol oynama olasılığı nedir?
✅ Çözüm:
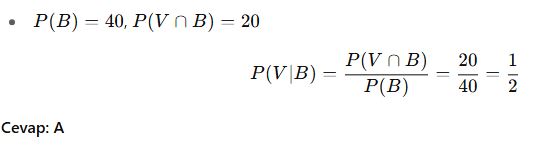
Bayes Teoremi
📌 Tanım
Bayes Teoremi, bir olayın gerçekleşme olasılığını, onunla ilgili elde edilen yeni bir bilgiye göre güncellemeye yarayan bir yöntemdir. Özellikle koşullu olasılıkların tersine çevrilmesinde kullanılır.
Bu formülde:
-
P(A∣B): B gerçekleştiğinde A’nın gerçekleşme olasılığı
-
P(B∣A): A gerçekleştiğinde B’nin gerçekleşme olasılığı
-
P(A): A olayının önsel (başlangıçtaki) olasılığı
-
P(B): B olayının toplam olasılığı
Gerçek Yaşam Bağlantısı
Bayes Teoremi, özellikle:
-
Tıp testlerinde (bir hastalığın test sonucu pozitif çıktığında gerçekten hasta olma olasılığı)
-
Güvenlik taramalarında
-
Makine öğrenmesinde
-
Oyun kuramı ve yapay zekâda
kullanılır.
Örnek:
Bir hastalığa sahip olma oranı %1, testin doğru pozitif verme oranı %99, yanlış pozitif verme oranı %5’tir.
Soru: Test sonucu pozitif gelen bir kişinin gerçekten hasta olma olasılığı nedir?
✅ Çözüm:
-
A: Kişi hasta
-
B: Test pozitif
Verilenler:

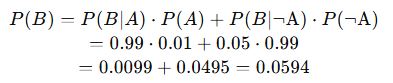
Şimdi Bayes Teoremi uygulanır:
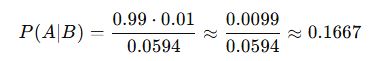
Yani test sonucu pozitif bile olsa, kişinin gerçekten hasta olma olasılığı yalnızca %16.7’dir!
Veriden Olasılığa Ünitesi Testi
1. Bir zar atılıyor. Zarın tek sayı gelmesi koşuluyla asal sayı gelme olasılığı kaçtır?
A) 1/6 B) 1/3 C) 1/2 D) 2/3
2. Bir torbada 5 kırmızı, 3 mavi top vardır. Bir top çekiliyor. Kırmızı olduğu biliniyorsa, bu topun mavi olmama olasılığı kaçtır?
A) 0 B) 1/5 C) 4/5 D) 1
3. Bir test, hastalıklı bireyleri %95 doğrulukla, sağlıklı bireyleri %90 doğrulukla tanımlıyor. Toplumda hastalık görülme oranı %1’dir. Test pozitif çıktığında, gerçekten hasta olma olasılığı yaklaşık nedir?
A) %9 B) %16 C) %50 D) %90
4. P(A) = 0,4 ve P(B|A) = 0,5 ise, P(A ∩ B) değeri kaçtır?
A) 0,1 B) 0,2 C) 0,3 D) 0,9
5. P(B) = 0,6 ve P(A ∩ B) = 0,3 ise, P(A|B) değeri kaçtır?
A) 0,2 B) 0,3 C) 0,4 D) 0,5
6. Bir torbada 3 kırmızı, 2 mavi top vardır. Geri koymadan 2 top çekiliyor. İlk topun kırmızı olduğu biliniyorsa, ikinci topun da kırmızı olma olasılığı nedir?
A) 1/5 B) 1/2 C) 2/5 D) 2/3
7. A ve B bağımsız olaylardır. P(A) = 0,3 ve P(B) = 0,4 olduğuna göre, P(A ∩ B) değeri kaçtır?
A) 0,7 B) 0,12 C) 0,1 D) 0,6
8. Bayes Teoremi, aşağıdakilerden hangisinde kullanılmaz?
A) Hastalık testleri
B) Trafik kazası sonrası hava yastığı açma ihtimali
C) Sayıların asal olup olmadığını belirleme
D) Güvenlik kontrolünde yolcunun riskli olup olmadığına karar verme
9. Koşullu olasılık tanımında yer alan P(A|B) ifadesi aşağıdakilerden hangisini ifade eder?
A) A ve B olaylarının aynı anda olma olasılığı
B) A olayının, B olayı gerçekleştiğinde olma olasılığı
C) A olayının bağımsız olma olasılığı
D) B olayının A’ya bağlı olma olasılığı
10. Aşağıdaki ifadelerden hangisi bağımsız olaylara örnektir?
A) Yağmur yağdığında şemsiye alma olasılığı
B) Elektrik kesilince jeneratörün devreye girme olasılığı
C) Bir zar atıldığında çift gelme ve yazı-tura atıldığında tura gelme
D) Bir öğrencinin derse geç kalması ile sınavdan düşük not alma
Veriden Olasılığa Testi Cevap Anahtarı:
-
B
-
D
-
B
-
B
-
D
-
B
-
B
-
C
-
B
-
C