AYT Matematik EBOB – EKOK Konu Anlatımı

AYT Matematik için oldukça önemli ve sık sorulan konulardan biri olan “EBOB – EKOK” ünitesine şimdi başlıyoruz. Bu konu, sadece çarpanlar üzerinden işlem yapmayı değil, mantık yürütme, problemleri modelleme ve sayı ilişkilerini kavrama becerilerini de test eder.

AYT Matematik – EBOB ve EKOK Giriş

🔍 Neden Önemlidir?

• Sayılar arasında ortak bölünebilme ilişkisi kurmak,
• Paylaştırma, eşleme, zamanlama problemleri çözmek,
• Sayı teorisi ve modüler aritmeğe geçiş için altyapı oluşturmak,
• Sınavlarda klasik problem tarzı olarak karşımıza çıkmakta.

TYT’de genelde işlem becerisi ölçülürken, AYT’de bu konudan gelen sorular daha çok problem tipi, yorumlama ve mantık zinciri kurma tarzındadır.

📌 Ünitedeki Alt Başlıklar

1. EBOB (En Büyük Ortak Bölen) Tanımı ve Hesaplanması
2. EKOK (En Küçük Ortak Kat) Tanımı ve Hesaplanması
3. EBOB ve EKOK Arasındaki Temel İlişki
4. EBOB-EKOK Kullanılarak Problem Çözme
5. Sayıların Aralarında Asal Olması ve Etkileri
6. Sayı Gruplarının Paylaştırılması (Kesme, Bölme, Dağıtma problemleri)
7. Zaman – Tekrar – Döngü Problemleri (LCM mantığıyla)

EBOB (En Büyük Ortak Bölen) – Tanımı ve Hesaplanması

📘 Tanım:

İki veya daha fazla sayıyı kalansız bölebilen en büyük doğal sayıya EBOB (En Büyük Ortak Bölen) denir.
Matematiksel gösterimi genelde şu şekildedir:

EBOB, özellikle sayıları ortak parçalara ayırma, eşit gruplara bölme ve en büyük birim belirleme gibi problemlerde kullanılır.

🎯 EBOB Hesaplama Yöntemleri:

✳️ Yöntem 1: Çarpanlara Ayırarak

Her sayının asal çarpanlarını bulup, ortak olan çarpanların küçük üslerini alarak çarpılır.

Örnek:

✳️ Yöntem 2: Bölme Yöntemi (Kısa Yol)

Sayıları yan yana yaz, ortak asal çarpanlarla sadeleştir, sonra ortak çarpanların çarpımı EBOB’tur.

Örnek:

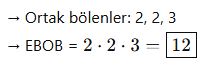
✳️ Yöntem 3: EBOB’un Özellikleri

• EBOB(a, b) = 1 ise: a ve b aralarında asaldır.
• EBOB(a, b) > 1 ise: a ve b ortak bölen içerir.

🧠 İpucu:

EBOB genellikle:

• Paylaştırma sorularında (eşit parça)
• Kesme – bölme problemlerinde
• Eşit uzunluk, alan vb. bölme sorularında
• Aralarında asal kavramının geçtiği sorularda karşımıza çıkar.

🎓 Örnek 1:

36 ve 48 sayılarının EBOB’u kaçtır?

🎓 Örnek 2:

Bir okulda 24 kız ve 36 erkek öğrenci vardır. Her grupta kız ve erkek sayısı eşit olacak şekilde en fazla kaç grup oluşturulabilir?

→ Her gruba eşit sayıda kız ve erkek düşmeli
→ Grup sayısı en fazla olacak → öğrencileri en küçük gruplara ayıracağız
→ O hâlde:

12 grup oluşturulabilir.
Her grupta:

• 24 ÷ 12 = 2 kız
• 36 ÷ 12 = 3 erkek

✅

EKOK (En Küçük Ortak Kat) – Tanımı ve Hesaplanması

📘 Tanım:

İki veya daha fazla sayının ortak katları arasında bulunan en küçük pozitif değere
EKOK (En Küçük Ortak Kat) denir.

Matematiksel gösterimi:

EKOK, özellikle eş zamanlı tekrar eden olaylar, eşit aralıklı döngüler, aynı anda bir yerde buluşma gibi problemlerde karşımıza çıkar.

🎯 EKOK Hesaplama Yöntemleri:

✳️ Yöntem 1: Asal Çarpanlara Ayırarak

Her sayının asal çarpanlarını bulup, tüm çarpanların en büyük üslerini alır ve çarparsınız.

Örnek:

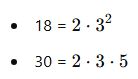
Tüm asal çarpanların en büyük üslerini al:

​

✳️ Yöntem 2: Ortak Bölme (Kısa Yol)

EBOB’taki gibi tablo yapılır. Bu kez tüm bölenlerle sadeleştir (ortak olmasa bile). En sonda tüm bölenler çarpılır.

Örnek:

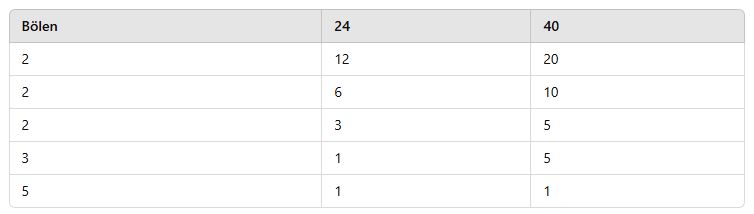
✳️ Yöntem 3: EBOB-EKOK Bağıntısı

AYT’de çok sorulan bir bağıntı vardır:

Bu sayede birini biliyorsanız diğerini kolayca bulabilirsiniz.

🎓 Örnek 1:

EBOB(18, 30) = 6 olduğuna göre, EKOK(18, 30) kaçtır?

🎓 Örnek 2:

İki işçi, biri 12 günde diğeri 18 günde bir işi tamamlamaktadır. İkisi birlikte işe başlarsa, aynı anda tekrar kaç gün sonra birlikte işe başlarlar?

→ İşin döngüsel tekrar etmesi → EKOK kullanılır:

Cevap: 36 gün sonra birlikte başlarlar. ✅

🧠 AYT İpuçları:

• EKOK → Aynı anda buluşma, birlikte olma, tekrar etme problemleri
• EBOB → Parçalara ayırma, eşit bölme, paylaştırma problemleri
• İfadelerde genelde:
  • “En az kaç?” → EKOK
  • “En fazla kaç?” → EBOB

EBOB – EKOK Arasındaki Temel İlişki ve Yorumlar

📘 Temel Bağıntı:

İki doğal sayı için geçerli olan en önemli ilişki:

​

Bu formül, hem işlem yaparken pratiklik kazandırır hem de ifade içeren sorularda büyük kolaylık sağlar.

🎓 Örnek 1:

EBOB(18, 30) = 6 ise, EKOK(18, 30) kaçtır?

🎓 Örnek 2:

EKOK(20, x) = 60 ve EBOB(20, x) = 5 ise, x kaçtır?

Formülü kullanalım:

📌 Özellikler ve Yorumsal Bilgiler:

🔹 Özellik 1:

a ile b aralarında asalsa, yani EBOB(a, b) = 1 ise:

Bu, çarpımları doğrudan EKOK’tur demektir.

🔹 Özellik 2:

a = b ise:

• EBOB(a, b) = a
• EKOK(a, b) = a
• Ürünleri = a²

🔹 Özellik 3:

a ve b’nin çarpımı değiştiğinde, EBOB ve EKOK ters orantılı değişir.

🎓 AYT Düzeyinde Yorumlu Soru:

Soru:

EBOB(a, b) = 5 ve EKOK(a, b) = 120 ise, a + b toplamının alabileceği en küçük değer kaçtır?

👉 Formül:

a ve b, 5’in katı olmalı (çünkü EBOB 5)
Deneyelim:

• a = 20, b = 30 ⇒ çarpım = 600
• a + b = 50 ✅
• Daha küçük a + b var mı?

Daha küçük deneyelim:

• a = 10, b = 60 ⇒ çarpım = 600
• a + b = 70 ❌ (daha büyük)
• a = 25, b = 24 ⇒ 25 × 24 = 600 ⇒ a + b = 49 ✅

Doğru cevap: 49​

Bu tip sorular deneme-yanılma + akıl yürütme ile çözülür.

🧠 Kritik Not:

• EBOB ve EKOK birlikte verildiğinde, sayıları asal çarpan ilişkileriyle kurgulayarak oluşturabilirsin.
• AYT sorularında “EBOB küçük olsun, EKOK büyük olsun” tarzı yorumlar sorulabilir.
• “EBOB(a, b) = d” ise, a = d·m, b = d·n şeklinde yazılabilir. Bu, çok sık kullanılan tekniktir.

EBOB – EKOK Kullanılarak Problem Çözme Teknikleri

Bu bölümde öğrendiğimiz EBOB ve EKOK hesaplamalarını gerçek hayattaki problem senaryolarında nasıl kullanacağımızı göreceğiz.

🟦 A. EBOB Kullanımı – Paylaştırma & Bölme Problemleri

EBOB, bir şeyi eş parçalara ayırmakla ilgilidir. Sorularda genellikle şu ifadeler kullanılır:

• “En büyük uzunluk”,
• “Eşit parçalara bölme”,
• “Artık kalmaması”,
• “En büyük parça”,
• “Kaç grup oluşturulur?”

Bu ifadeler varsa, çözümde EBOB kullanılır.

🎓 Örnek 1:

72 cm ve 96 cm uzunluğundaki iki kumaş parçası, eşit uzunlukta ve en uzun olacak şekilde parçalara ayrılmak isteniyor. Kaç parça kumaş elde edilir?

→ Ortak uzunlukların en büyüğü:

• 72 ÷ 24 = 3 parça
• 96 ÷ 24 = 4 parça

Toplam parça sayısı = 3 + 4 = 7

🎓 Örnek 2:

Bir okulda 48 matematik ve 64 fizik kitabı vardır. Kitaplar türlerine göre karıştırılmadan kutulara eşit sayıda konulacaktır. Her kutuda aynı türden kitap olacak şekilde en fazla kaç kutu kullanılır?

🟦 B. EKOK Kullanımı – Zamanlama & Buluşma Problemleri

EKOK, tekrar eden olaylarda veya aynı anda buluşmaların hesaplandığı problemlerde kullanılır.

Sorularda genelde şu ifadeler geçer:

• “Aynı anda tekrar”,
• “Birlikte başlarlar”,
• “Kaç gün sonra tekrar karşılaşırlar?”,
• “Zil çalıyor, saat çalıyor” gibi.

🎓 Örnek 3:

Bir otobüs her 24 dakikada, bir başka otobüs her 36 dakikada bir duraktan geçmektedir. İkisi de aynı anda geçtiyse, kaç dakika sonra tekrar birlikte geçerler?

🎓 Örnek 4:

Üç zil sırasıyla 12, 18 ve 30 dakikada bir çalıyor. Üçü de aynı anda çaldıktan sonra en erken kaç dakika sonra tekrar birlikte çalarlar?

🧠 AYT Seviyesi İpucu:

Sorularda en fazla → EBOB,
en az → EKOK
diyerek başlangıçta hangi yöntemi kullanacağımızı kolayca seçebiliriz.

🎓 Örnek 5 (Karma Problem):

Bir çiftlikte 120 tavuk ve 180 ördek bulunmaktadır. Hayvanlar, türlerine göre karıştırılmadan eşit sayıda kümelere ayrılacaktır. Her kümeye aynı türden hayvan konulacaksa, bir kümeye en fazla kaç hayvan konulabilir?

​

• 120 ÷ 60 = 2 tavuk kümesi
• 180 ÷ 60 = 3 ördek kümesi
  → Toplam 5 küme

Aralarında Asal Sayılar ve EBOB – EKOK Üzerindeki Etkileri

📘 Tanım: Aralarında Asal Sayılar

İki doğal sayı sadece 1’e bölünebiliyorsa, yani EBOB’ları 1 ise, bu sayılara aralarında asal denir.

Örnekler:

• (3, 8) → aralarında asal ✅
• (10, 15) → ortak bölen 5 → aralarında asal değil ❌

Not: Sayıların kendisi asal olmak zorunda değildir. Önemli olan birbirlerine göre asal olmalarıdır.

🧠 Temel Özellik:

Eğer a ve b aralarında asalsa, şu özdeşlik geçerlidir:

Bu, AYT’de çok sık çıkan ve doğru kurulması gereken kritik bir ilişkidir.

🎓 Örnek 1:

a ve b pozitif tam sayılar, EBOB(a, b) = 1 ve a · b = 120 ise, EKOK(a, b) kaçtır?

🎓 Örnek 2:

EBOB(x, 18) = 1 olacak şekilde 1 < x < 20 koşulunu sağlayan kaç farklı x vardır?

Yani: 1 ile 20 arasındaki sayılardan, 18 ile aralarında asal olanlar sayılacak.

→ 18’in asal çarpanları: 2 ve 3
→ Bu asal çarpanlarla ortak olmayan sayılar aranır.

1–20 arası 18 sayı var.
18 ile ortak bölenleri olanları eleyelim:

• 2 ile bölünen: 2, 4, 6, 8, 10, 12, 14, 16, 18 → 9 adet
• 3 ile bölünen: 3, 6, 9, 12, 15, 18 → 6 adet
• Hem 2 hem 3 ile bölünen (yani 6 ile bölünenler): 6, 12, 18 → 3 adet

Inclusion-Exclusion kullan: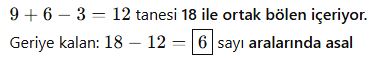

🎯 AYT Tarzı Yorumsal Soru:

Soru:

EBOB(a, b) = 4 ve EKOK(a, b) = 120 ise, a + b toplamının alabileceği en küçük değer kaçtır?

Verilen:

a ve b, 4’ün katıdır.
a = 4x, b = 4y olsun ⇒

Şimdi x + y en küçük olacak şekilde, xy = 30 olan sayı çarpanlarını deneyelim:

• x = 1, y = 30 ⇒ x + y = 31
• x = 2, y = 15 ⇒ x + y = 17
• x = 3, y = 10 ⇒ x + y = 13
• x = 5, y = 6 ⇒ x + y = 11 ✅
  (5 ve 6 aralarında asal mı? Evet!)

a = 4·5 = 20
b = 4·6 = 24
a + b = 44 → Cevap: 44​ ✅

🧠 Unutma:

• EBOB küçükse → sayılar daha çok çarpan içerir.
• EKOK büyükse → sayıların birlikte katı daha geç gelir.
• Sayılar aralarında asal olduğunda → EBOB = 1, EKOK = çarpım

Zaman – Döngü – Tekrar Problemleri (EKOK Uygulamaları)

Bu tür sorular genellikle “eş zamanlı olaylar”, “buluşma”, “zil çalma”, “tekrar eden işlemler” gibi senaryolar içerir.

🎯 Bu tür sorularda genellikle sorulan:

• “Kaç dakika/gün sonra tekrar birlikte olur?”
• “Bir işi tekrar yapmak için en erken kaç dakika gerekir?”
• “Aynı anda başlayan iki döngü ne zaman tekrar aynı anda başlar?”

İşte bu soruların çözüm yolu: EKOK’tur. Çünkü tekrar eden olayların en küçük ortak tekrar zamanını bulmak gerekir.

📘 Genel Kural:

​

Buradaki a ve b → olayların tekrar süreleridir.

🎓 Örnek 1:

Ali 15 dakikada bir, Veli 20 dakikada bir egzersiz yapmaktadır. İkisi birlikte saat 09:00’da egzersize başladığına göre, en erken kaç dakika sonra birlikte tekrar egzersiz yaparlar?

Cevap: 60 dakika sonra → 10:00’da ✅

🎓 Örnek 2:

Üç zil sırasıyla 18, 24 ve 30 dakikada bir çalmaktadır. Ziller aynı anda çaldıktan kaç dakika sonra tekrar birlikte çalarlar?

• EKOK(18, 24) = 72
• EKOK(72, 30) = 360

Cevap: 360 dakika sonra → 6 saat sonra ✅

🎓 Örnek 3 – Zamanlı Saat Problemi:

Bir zil 40 dakikada bir, diğer zil 60 dakikada bir çalmaktadır. Ziller saat 07:30’da birlikte çalmıştır. En erken saat kaçta tekrar birlikte çalarlar?

07:30 + 2 saat = 09:30

🎓 Örnek 4 – Geri Sayım Problemi:

Bir trafik lambası 45 saniyede bir kırmızıya, bir diğeri 75 saniyede bir kırmızıya dönmektedir. Aynı anda kırmızı yandıklarında en erken kaç saniye sonra tekrar aynı anda kırmızı yanar?

🧠 Problem Tipleri – Soru Tarzları:

📌 Ekstra İpucu:

Bazen EKOK’la çözülecek sorular dakika değil saat cinsinden, gün olarak, hatta ay olarak sorulabilir. Birim dönüşüm dikkat ister!

AYT Matematik EBOB – EKOK Deneme Soruları

1.

EBOB(36, 60) kaçtır?

A) 6  B) 12  C) 18  D) 24

2.

EKOK(24, 36) işleminin sonucu kaçtır?

A) 72  B) 108  C) 144  D) 96

3.

EBOB(a, b) = 5, EKOK(a, b) = 120 ise, a · b çarpımı kaçtır?

A) 600  B) 125  C) 240  D) 580

4.

EBOB(15, x) = 1 ve x < 20 koşulunu sağlayan kaç farklı pozitif tam sayı vardır?

A) 4  B) 6  C) 8  D) 10

5.

Bir öğrenci 36 dakikada bir, bir başka öğrenci 60 dakikada bir kitap okuyor. İkisi birlikte 08:00’de okuma yapıyorlar. Bir sonraki aynı anda okuma ne zaman olur?

A) 09:00  B) 10:00  C) 11:00  D) 12:00

6.

Bir eşya 42 gün ve 63 günde bir bakım gerektiriyor. İlk bakım birlikte yapıldığına göre, tekrar birlikte bakım kaç gün sonra yapılır?

A) 84  B) 126  C) 168  D) 189

7.

Bir çubuğun uzunluğu 84 cm, bir diğerinin 108 cm’dir. Bu çubuklar en uzun ve eşit parçalara ayrılmak isteniyor. Parça uzunluğu kaç cm olur?

A) 6  B) 8  C) 12  D) 24

8.

EKOK(18, x) = 90 ve EBOB(18, x) = 3 ise, x kaçtır?

A) 15  B) 30  C) 45  D) 60

9.

EBOB(a, b) = 1 ise, EKOK(a, b) değeri aşağıdakilerden hangisine eşittir?

A) a + b
B) a · b
C) a² + b²
D) a – b

10.

Bir okulda 180 kız ve 144 erkek öğrenci vardır. Her grupta eşit sayıda ve yalnızca aynı cinsiyetten öğrenci olacak şekilde en fazla kaç grup oluşturulabilir?

A) 6  B) 8  C) 12  D) 36

✅ Cevap Anahtarı

1. B → 36 ve 60’ın EBOB’u 12
2. A → EKOK(24,36) = 72
3. A → 5×120 = 600
4. C → 1–19 arası, 15 ile aralarında asal olanlar = 8 adet
5. A → EKOK(36,60) = 180 dk = 3 saat → 11:00
6. B → EKOK(42,63) = 126 gün
7. C → EBOB(84,108) = 12
8. B → 18·x = 90·3 → x = 270/18 = 15
9. B → Aralarında asal ise EKOK = a·b
10. D → EBOB(180,144) = 36