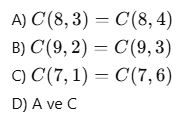AYT Permütasyon ve Kombinasyon Konu Anlatımı

Bu ünite, verilen nesnelerin sıralama (permütasyon) ve seçim (kombinasyon) yollarını saymaya yöneliktir.
AYT’de bu konular:

• Temel Sayma Kuralları

• Permütasyon kavramı ve formülleri

• Kombinasyon kavramı ve özellikleri

• Şarta bağlı durumlar

• Yer değiştirme, tekrar, özel koşullu seçimler

• Olasılık ile bağlantılı yorumlar
  başlıklarıyla karşımıza çıkar.

🔹 Ünitenin Alt Başlıkları:

1. Temel Sayma Kuralları (Çarpma – Toplama)

2. Permütasyon

3. Aynı Tür Nesnelerin Permütasyonu

4. Permütasyonlu Problemler

5. Kombinasyon

6. Kombinasyonlu Problemler

7. Pascal Üçgeni ve Özellikleri

🎯 AYT’de Bu Konu Nasıl Sorulur?

• Verilen koşullara göre kaç farklı sıralama/yerleştirme yapılır?

• Hangi sayıda grup oluşturulabilir?

• Sıralamada/tercihte tekrar var mı yok mu?

• Belirli şartları sağlayan permütasyon/kombinasyonlar

• Olasılık ve istatistik sorularının içinde dolaylı olarak yer alır

Temel Sayma Kuralları (Çarpma ve Toplama)

📘 A. Toplama Kuralı (Veya Durumu)

İşlemler birbirini dışlıyorsa (aynı anda yapılmıyorsa), toplam kuralı kullanılır.

Eğer A işi m yolla,
B işi $n$ yolla yapılıyorsa
ve bu işler aynı anda yapılamıyorsa:

Toplam yol sayısı= m+n

🎓 Örnek 1 (Toplama Kuralı):

Bir öğrenci:

• Matematik sınavına 3 farklı kalemle,

• Türkçe sınavına 2 farklı kalemle girebiliyor.

Ama aynı anda sadece bir sınava girebiliyor.

📘 B. Çarpma Kuralı (Ve Durumu)

İşlemler birlikte yapılabiliyorsa (aynı anda seçiliyorsa), çarpma kuralı kullanılır.

Eğer A işi m yolla,
her A işine karşılık B işi $n$ yolla yapılabiliyorsa:

Toplam yol sayısı= m⋅n

🎓 Örnek 2 (Çarpma Kuralı):

Bir öğrenci:

• 3 gömlek,

• 4 pantolon arasından seçim yapıyor.
  Her gömlek, her pantolonla giyilebilir:

📘 C. Karma Uygulama:

Bazı sorular hem toplama hem çarpma kuralını içerir.

🎓 Örnek 3:

Ali ya sinemaya gidecek (3 film seçeneği var)
ya da arkadaşına gidecek (2 arkadaş seçeneği ve her biriyle 2 aktivite yapılabiliyor).

• Sinema → 3 yol

• Arkadaş → 2 arkadaş × 2 aktivite = 4 yol
  → Toplam yol: 3+4=7

🧠 Özet:

Mini Alıştırmalar:

1. Bir öğrenci 2 farklı kalem, 3 farklı silgi alabilir. Kaç farklı şekilde 1 kalem ve 1 silgi seçebilir?

2. 5 farklı tişört veya 2 farklı gömlek giyebilen biri kaç farklı şekilde giyinebilir?

3. 3 farklı yol, her yolda 4 otobüs varsa, kaç farklı ulaşım seçeneği olur?

Permütasyon

📘 Permütasyon Nedir?

Permütasyon, bir kümeden seçilen elemanların sıralı dizilişlerinin sayısını ifade eder.

Yani:

• Nesneler seçilir

• Seçilenler sıralanır

• Sıra önemli

🧠 Temel Permütasyon Formülü:

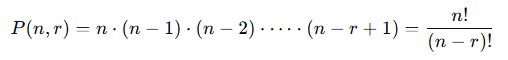
🎯 Önemli Özellikler:

• Permütasyonda elemanlar tekrarsızdır

• Her farklı sıra farklı bir permütasyondur

🎓 Örnek 1:

5 kişilik bir gruptan 3 kişi seçilip sıralanacak. Kaç farklı sıra oluşur?

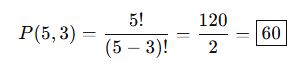
🎓 Örnek 2:

Ali’nin 4 farklı kitabı var. Bu kitapları tümünü bir rafa farklı sıralarla dizerse kaç farklı diziliş olur?

📘 Tüm Elemanlar Sıralanırsa:

📌 Permütasyon vs Kombinasyon:

Mini Alıştırmalar:

1. 6 kişi arasından 2 kişi seçilip sıralanırsa kaç farklı sıralama olur?

2. 7 kişilik bir ekipten başkan ve başkan yardımcısı seçilecek. Kaç farklı şekilde olabilir?

3. 5 harfli bir kelimenin harfleri farklı şekilde kaç şekilde dizilir?

Aynı Tür Nesnelerin Permütasyonu

📘 Tanım:

Bir grupta bazı elemanlar aynıysa, bu elemanların birbirine karışması aynı diziliş sayılır.
Bu durumda normal permütasyondan, tekrar edenlerin permütasyonu kadar bölme yapılır.

Formül:

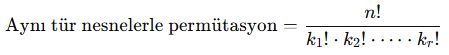
🎓 Örnek 1:

“KAZAK” kelimesinin harfleri kaç farklı şekilde sıralanabilir?

• 5 harf var → n=5

• “K” harfi 2 kez tekrar ediyor

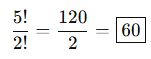
🎓 Örnek 2:

“ANANAS” kelimesinin harfleriyle kaç farklı sıralama yapılabilir?

• 6 harf

• A: 3 kez

• N: 2 kez

• S: 1 kez

📌 Not:

• Tüm harfler/farklı nesneler farklıysa → klasik permütasyon

• Tekrar varsa → bu formül kullanılır

Mini Alıştırmalar:

1. “MAMA” kelimesi kaç farklı şekilde yazılabilir?

2. “BALABAN” kelimesinde toplam kaç farklı diziliş yapılabilir?

3. 4 kırmızı, 3 mavi top bir sıraya kaç farklı şekilde dizilebilir?

Permütasyonlu Problemler

📘 Konu Özeti:

Permütasyon problemleri, belirli şartlar altında yapılan sıralamaları inceler.
Bu sorularda genellikle:

• Yan yana/ayrı durma

• Başta/sonda bulunma

• Belirli elemanların yeri sabit

• Belli kişiler birlikte/ayrı oturacak gibi
  durumlar vardır.

🎯 Soru Tiplerine Göre Strateji:

🔹 A. Belirli bir kişi/nesne başta ya da sonda:

Toplam permütasyon:
(n−1)!

Örnek:
5 kişi bir sıraya diziliyor. Ali başta olacaksa:

🔹 B. İki kişi yan yana oturacaksa:

1 blok gibi düşünülür
Sonra blok içi kendi içinde sıralanır

Örnek:
6 kişi, Ahmet ve Ayşe yan yana:

• Blok olarak 5 kişi → 5!

• Blok içi: 2!

🔹 C. İki kişi yan yana gelmeyecek:

Tüm sıralama – yan yana sıralama

Örnek:
Yukarıdaki örnekte, Ahmet ve Ayşe yan yana gelmesin:

• Tüm diziliş: 6! = 720

• Yan yana diziliş: 240

🔹 D. Belirli kişilerin yeri sabitse:

Sabit kişiyi yerine koy, kalanları sırala

Örnek:
7 kişilik sırada Ayşe ortada → geri kalan 6 kişi:

🎓 Örnek Soru:

4 erkek ve 2 kız bir sıraya dizilecek.
Kızlar yan yana oturmak zorundaysa, kaç farklı sıralama yapılabilir?

• Kızlar blok: 1

• Erkekler: 4 kişi + 1 blok = 5!

• Blok içi: 2!

Mini Problemler:

1. 5 kişi bir sıraya dizilecek. Ahmet sonda olacaksa kaç farklı sıralama olur?

2. 6 kişi, Ali ve Ayşe yan yana oturacak → kaç farklı sıralama?

3. 6 kişi, Ali ve Ayşe yan yana oturmayacak → kaç farklı sıralama?

Kombinasyon

📘 Kombinasyon Nedir?

Kombinasyon, bir kümeden belirli sayıda eleman seçmek ama sıralamadan bağımsız olarak değerlendirmektir.

Sadece hangi elemanlar seçildiği önemlidir, hangi sırayla seçildikleri önemli değildir.

🧠 Temel Formül:

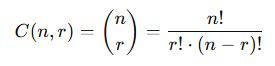
Burada:

• n: Toplam eleman sayısı

• r: Seçilecek eleman sayısı

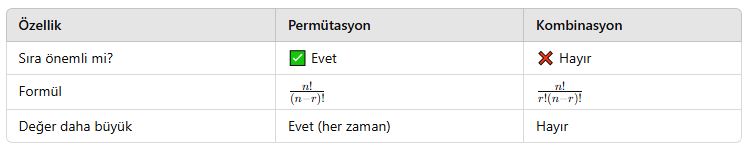
🎯 Permütasyon vs Kombinasyon

🎓 Örnek 1:

Bir grupta 6 kişi var. Bu gruptan 3 kişi seçilecek, sıralama önemli değil.

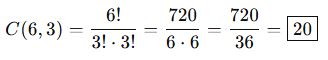
🎓 Örnek 2:

Bir sınıfta 10 öğrenci var. 2 kişi sınıf temsilcisi olarak seçilecek (sıra yok).

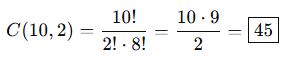
📌 Önemli Özellikler:

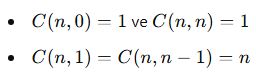
• Simetrik özelliği:

Mini Alıştırmalar:

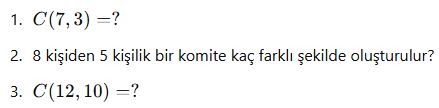
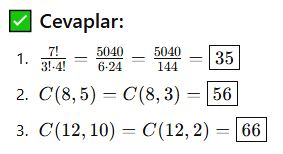
Kombinasyonlu Problemler

📘 Konu Özeti:

Bu başlıkta:

• Belirli elemanlar seçilecek

• Belirli kişiler dahil/harici tutulacak

• Belirli şartlar sağlanarak seçim yapılacak

• Gruplama, eşit dağıtma gibi durumlar olacak

🎯 Soru Tipi 1: Zorunlu Dahil veya Hariç

🎓 Örnek:

10 kişilik gruptan 4 kişilik bir komite seçilecek.
Ahmet bu komitede mutlaka olacaksa, kaç farklı seçim yapılabilir?

→ Ahmet sabit → geriye 3 kişi daha seçilecek, kalan 9 kişi arasından:

🎯 Soru Tipi 2: Birlikte veya Ayrı Seçim

🎓 Örnek:

8 kişilik gruptan 3 kişi seçilecek.
Ali ve Ayşe birlikte seçilecekse, kaç seçim yapılabilir?

→ Ali & Ayşe sabit → geriye 1 kişi seçilecek → kalan 6 kişi içinden:

​

Ayrı seçilsin denirse:
→ Ali ve Ayşe birlikte olmayacak
→ Tüm seçimlerden birlikte oldukları durum çıkartılır

​

🎯 Soru Tipi 3: Farklı Gruplara Ayırma

🎓 Örnek:

6 kişi, 2 kişilik ve 4 kişilik iki ayrı gruba ayrılacak.
Kaç farklı grup oluşturulabilir?

1. 2 kişilik grubu seç: C(6,2)=15

2. Geri kalan 4 kişi otomatik belirlenir

🎯 Soru Tipi 4: Aynı cins elemanla farklı gruplar

🎓 Örnek:

10 kişilik bir sınıftan 3 kişilik 2 farklı grup oluşturulacak.
Her gruba aynı kişi alınamaz. Kaç farklı durum?

1. İlk grup: C(10,3)

2. İkinci grup: kalan 7 kişi → C(7,3)

​

Mini Problemler:

1. 9 kişiden 4 kişilik ekip kurulacak. Ahmet alınmayacak.
   → Kaç farklı ekip oluşturulur?

2. 7 kişiden 3 kişi seçilecek. Ali ve Ayşe aynı grupta olmayacak.
   → Kaç farklı seçim?

3. 6 kişilik gruptan 2 kişilik farklı iki ekip oluşturulacak.
   → Kaç farklı durum?

Pascal Üçgeni ve Özellikleri

📘 Pascal Üçgeni Nedir?

Pascal üçgeni, kombinasyon katsayılarının üçgen şeklinde sıralandığı bir yapıdır.
Her sayı, bir üst satırdaki iki sayının toplamıdır.

🧠 Yapılışı:

Başlangıç:

• Her satırın ilk ve son terimi 1’dir

• Ortadaki her terim:

🎯 Kombinasyonla Bağlantısı:

Örnek:
Satır 4:

📌 Özellikler:

1. Simetriktir:

2. Toplam özelliği:
   Her satırın toplamı:

Örneğin:

3. Bir satır aşağıya geçmek için:
   Her terim:

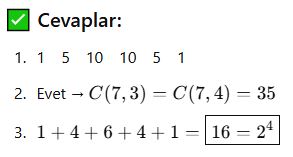
AYT Permütasyon ve Kombinasyon Testi

Cevap anahtarı en altta
Her soru farklı bir alt başlıkla ilişkilidir 👇

1. (Temel Sayma Kuralları)

Bir öğrenci 3 farklı kalem ve 2 farklı silgiden bir kalem ve bir silgi seçecektir.
Kaç farklı seçim yapılabilir?

A) 3 B) 5 C) 6 D) 10

2. (Permütasyon)

8 kişilik bir gruptan başkan, başkan yardımcısı ve sekreter seçilecektir.
Kaç farklı atama yapılabilir?

A) 336 B) 512 C) 720 D) 120

3. (Tüm elemanların permütasyonu)

“ANKARA” kelimesinin harfleri kaç farklı şekilde dizilebilir?

A) 120 B) 360 C) 720 D) 60

4. (Aynı tür nesnelerin permütasyonu)

“MADAM” kelimesi kaç farklı şekilde yazılabilir?

A) 60 B) 30 C) 20 D) 10

5. (Koşullu permütasyon)

6 kişi bir sıraya dizilecektir. Ahmet ve Ayşe yan yana oturacaksa, kaç farklı sıralama olur?

A) 240 B) 480 C) 720 D) 1440

6. (Kombinasyon)

10 kişilik bir gruptan 3 kişilik bir ekip kaç farklı şekilde seçilebilir?

A) 120 B) 60 C) 90 D) 45

7. (Koşullu kombinasyon)

8 kişilik bir ekipten 4 kişilik bir ekip oluşturulacak. Ayşe bu ekipte olmak zorundaysa, kaç farklı seçim yapılabilir?

A) 35 B) 70 C) 56 D) 84

8. (Birlikte seçilme durumu)

7 kişilik bir gruptan 3 kişilik ekip seçilecektir. Ali ve Veli birlikte seçilecekse kaç farklı ekip oluşturulabilir?

A) 5 B) 6 C) 7 D) 8

9. (Pascal üçgeni)

Pascal üçgeninde 6. satırın 2. terimi nedir?
(İlk terim C(6,0) kabul edilir.)

A) 6 B) 15 C) 20 D) 10

10. (Simetrik kombinasyon özelliği)

Aşağıdakilerden hangisi doğrudur?