AYT Matematik Polinomlar Konu Anlatımı

Polinomlar, matematikte değişkenli ifadeleri düzenli bir kurala göre yazma ve işlem yapma biçimidir.
Bu ünitede:

• Polinom tanımı ve derecesi

• Polinom türleri

• Polinomlarda toplama – çıkarma – çarpma

• Polinom bölmesi ve kalan

• Eşitlik ve katsayı karşılaştırmaları

• Polinomla denklem kurma
  gibi konular yer alır.

🔹 Polinomlar Ünitesinin Alt Başlıkları:

1. Polinom Tanımı ve Terim Yapısı

2. Polinomların Derecesi

3. Polinomlarda Dört İşlem

4. Polinom Bölmesi – Kalan Bulma

5. Polinomlarda Eşitlik – Denklem Kurma

6. Polinom Grafikleri ve Yorum

🎯 AYT’de Bu Konu Nasıl Sorulur?

• Verilen ifadeye göre polinomun derecesini belirleme

• Katsayı karşılaştırması ve bilinmeyen bulma

• Bölme ve kalan hesaplaması

• Polinom eşitliğinden bilinmeyenleri bulma

• f(x) türünden sorularla polinomu tanıma

• Grafiksel yorum soruları

Polinom Tanımı ve Terim Yapısı

📘 Polinom Nedir?

Polinom; bir veya birden fazla terimden oluşan, her terimin:

• Değişkenin doğal sayı kuvvetini içerdiği

• Katsayılarının gerçek sayı olduğu cebirsel ifadelerdir.

Polinomun Genel Yazımı:

Bir değişkenli polinom:

🎓 Örnek:

• Baş katsayı: 5

• Derece: 3

• Sabit terim: –4

• Katsayılar: 5, –2, 7, –4

❌ Polinom Olamayan İfadeler:

Aşağıdaki ifadeler polinom değildir, çünkü:

✅ Polinom Olan – Olmayan Karşılaştırması:

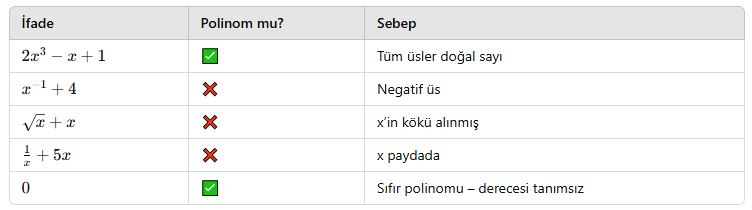
📌 Önemli Notlar:

• Sabit bir sayı da polinomdur. Örneğin: P(x)=3

• Sıfır polinomu özel durumdur, çünkü derecesi tanımsızdır

Mini Alıştırmalar:

Aşağıdaki ifadelerin polinom olup olmadığını ve varsa derecelerini belirtin

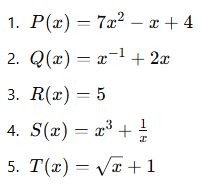
✅ Cevaplar:

1. ✅ Polinom – Derece: 2

2. ❌ Negatif kuvvet – polinom değil

3. ✅ Polinom – Derece: 0

4. ❌ Değişken paydada – polinom değil

5. ❌ Kök içeriyor – polinom değil

Polinomların Derecesi

📘 Derece Nedir?

Bir polinomda, değişkenin en yüksek doğal sayı üssü, o polinomun derecesidir.

🧠 Genel Kural:

🎯 Tek Değişkenli Polinomlarda:

Örnek:

🎯 Sabit Polinomlarda:

Sabit sayı varsa → derece = 0
Ama:

🎯 Çok Değişkenli Polinomlarda:

Birden fazla değişken varsa (örneğin x,y):

• Her terimdeki değişken üssü toplamına bakılır

• En yüksek toplam → polinomun derecesidir

Örnek:

🎓 Terim Derecesi vs Polinom Derecesi:

• Her terimin kendi derecesi olabilir

• Polinomun derecesi, en büyük terim derecesidir

Mini Alıştırmalar:

Verilen ifadelerin derecesini bulun:

Polinomlarda Dört İşlem (Toplama – Çıkarma – Çarpma – Sabitleme)

📘 A. Polinomlarda Toplama – Çıkarma

Polinomlarda toplama ve çıkarma, benzer dereceli terimler arasında yapılır.
Yani aynı dereceli terimlerin katsayıları toplanır ya da çıkarılır.

🎓 Örnek:

Verilsin:

Toplama:

Çıkarma:

📘 B. Polinomlarda Çarpma

Polinomlar dağıtma yöntemiyle çarpılır.
Dereceler toplanır.

🎓 Örnek:

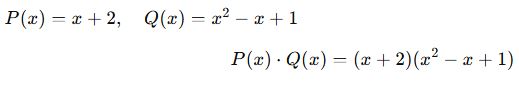
Adım adım:

Toplanır:

📘 C. Sabit Bir Sayı ile Değerlendirme (P(a) Bulma)

Bir polinomda x yerine sayı yazılarak değer bulunur.

🎓 Örnek:

📌 Dikkat:

• Çarpma işleminde her terim her terimle çarpılır

• Derece toplama ile artar:
  

• P(a) ifadesi, kalan bulmada da çok önemlidir (ileride göreceğiz)

Polinom Bölmesi ve Kalan Bulma

📘 A. Polinom Bölmesi Nedir?

Bir polinomun, başka bir polinoma bölünmesiyle:

şeklinde yazılır.

Yani:

• P(x) → bölünen

• D(x) → bölen

• Q(x) → bölüm

• R(x) → kalan

• Kalanın derecesi, bölenin derecesinden küçük olmak zorundadır

📘 B. Özel Kural – Kalan Bulma (P(a) Kuralı)

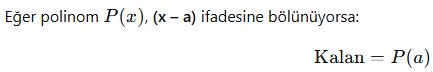
Bu yöntem, bölme işlemine gerek kalmadan kalanı direkt bulmayı sağlar.

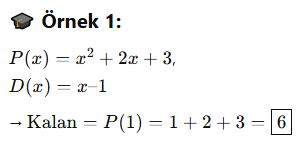
📘 C. Uzun Yoldan Bölme (Klasik İşlem)

Verilsin:

Adım adım klasik bölme yapılır. Kalan sıfırsa, bu aynı zamanda tam bölünüyor anlamına gelir.

🎓 Örnek 3: Eşitlikli Soru

Verilsin:

→ Bu ifade, (x – 2)’ye bölündüğünde kalan 7’dir, çünkü:

Polinomlarda Eşitlik ve Denklem Kurma

📘 Temel Yöntem: Katsayı Karşılaştırma

Eğer iki polinom birbirine eşitse:

O zaman aynı dereceli terimlerin katsayıları birbirine eşittir.

Bu yöntemle bilinmeyen katsayılar bulunabilir.

🎯 Kural:

🎓 Örnek 1:

Verilsin:

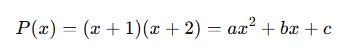
Çarpalım:

🎓 Örnek 2:

Verilsin:

Yine önce açalım:

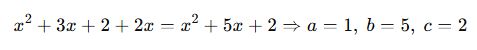
📘 Bilinmeyenli Katsayı Sorusu:

Verilsin:

eşitliğine göre:

Bu tarz sorular çok çıkıyor. Bilinmeyen katsayıyı karşılıklı eşitleyerek buluruz.

🎓 Örnek 3 – Bilinmeyenli Sorular:

Verilsin:

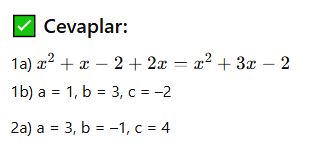
Polinom Grafikleri ve Yorum

📘 Polinom Grafiği Nedir?

Bir polinom fonksiyonunun grafiği,

eşitliğine göre çizilen x–y düzlemindeki eğridir.

Polinom grafikleri, polinomun derecesine göre farklı davranışlar gösterir.

🔹 A. Dereceye Göre Grafik Şekli

Çift dereceli polinomlar (2, 4, 6…) → uçlar aynı yöne
Tek dereceli polinomlar (1, 3, 5…) → uçlar zıt yönlere

🔹 B. Kökler ve Grafik İlişkisi

Bir polinomun kökleri, grafiğin x-eksenini kestiği noktalardır.

• P(x)=0 çözümleri = x-eksenini kestiği yerler

• Kök sayısı, grafiğin kaç noktada x-eksenini kestiğini gösterir

🎓 Örnek:

• Kökler: x = 1, x = –2

• Parabol grafiği x-eksenini –2 ve 1’de keser

• Baş katsayı pozitif → yukarı bakan parabol

🔹 C. Sabit Terim – y Ekseni Kesişimi

Polinomda sabit terim
grafiğin y-eksenini kestiği noktadır.

Yani:

🔹 D. Tepe Noktası (2. derece için)

• Tepe noktası x değeri:

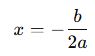
📈 Grafiksel İpuçları:

Ayt Polinomlar Deneme Testi

Her soru farklı bir alt başlıktan seçilmiştir.
Cevap anahtarı en altta.

1. (Polinom Tanımı)

Aşağıdakilerden hangisi polinom değildir?

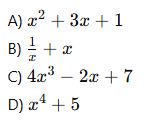
2. (Derece Belirleme)

A) 2 B) 3 C) 4 D) 5

3. (Sabit Polinom)

Aşağıdaki ifadelerden hangisinin derecesi tanımsızdır?

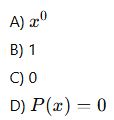
4. (Toplama İşlemi)

Verilsin:

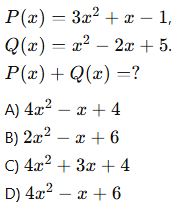
5. (Çarpma İşlemi)

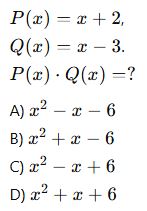
6. (Sabit Terim Bulma)

polinomunun sabit terimi kaçtır?

A) –2 B) –1 C) 1 D) 2

7. (Kalan Bulma)

A) 2 B) 4 C) 5 D) 6

8. (Katsayı Belirleme)

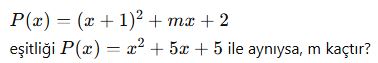
A) 1 B) 2 C) 3 D) 4

9. (Grafik – Kök Sayısı)

A) 0 B) 1 C) 2 D) 3

10. (Tepe Noktası)

A) 1 B) 2 C) 3 D) 4