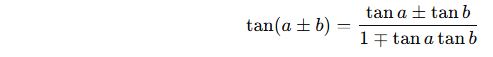AYT Matematik Trigonometri Konu Anlatımı

Trigonometri; üçgenler, daireler ve açılar arasında oranlara dayalı ilişkileri inceler.
AYT düzeyinde, bu bilgiler artık sadece dik üçgenle sınırlı değildir:

• Tüm açı değerleri için tanım

• Birim çember ve trigonometrik oranlar

• Grafikler, dönüşümler, eşitlikler

• Trigonometrik denklemler ve özdeşlikler

• Açılar arasındaki ilişkiler (toplam, fark, iki katı, yarım açı)

• Trigonometrik denklem çözme

konu kapsamına girer.

🔹 Ünitenin Alt Başlıkları:

1. Trigonometrik Oranlar (Dik Üçgende)

2. Trigonometrik Fonksiyonlar ve Birim Çember

3. Trigonometrik Fonksiyonların Özellikleri ve Grafikler

4. Trigonometrik Eşitlikler ve Özdeşlikler

5. Açılarla İlgili Formüller (Toplam-Fark, 2 Katı, Yarım Açı)

6. Trigonometrik Denklemler ve Çözüm Kümeleri

Trigonometrik Oranlar (Dik Üçgende)

📘 Tanım:

Trigonometrik oranlar, dik üçgenlerde bir açıya göre kenar uzunlukları arasındaki oranlarla tanımlanır.

Bir dik üçgende:

• Hipotenüs: Dik kenarların karşısındaki kenar (en uzun)

• Komşu kenar: Açının yanında olan dik kenar

• Karşı kenar: Açının karşısındaki dik kenar

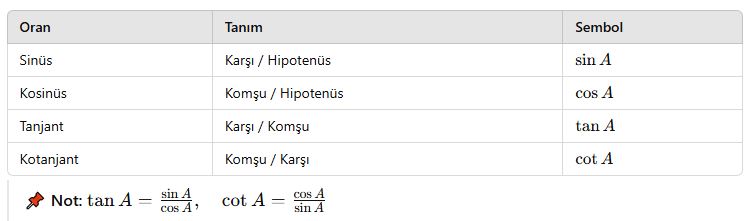
📘 Oranlar:

Bir dik üçgende A açısına göre:

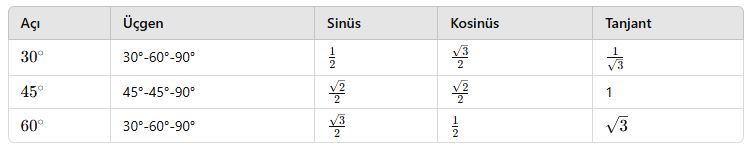
📘 Özel Üçgenler:

📘 Pisagor Bağıntısı:

​

Bu bağıntı AYT’de özdeşlik olarak da sıkça kullanılır.

Trigonometrik Fonksiyonlar ve Birim Çember

📘 A. Birim Çember Nedir?

• Merkezi orijinde olan, yarıçapı 1 birim olan çemberdir.

• Denklemi:

​

• Açı, x ekseninden itibaren saat yönünün tersine ölçülür

• Her açı bir noktaya, o nokta da bir trigonometrik değere karşılık gelir

📘 B. Trigonometrik Fonksiyonların Tanımı (Genel Açı için)

Birim çemberde r = 1 olduğundan:

🎯 Kısaca:

Birim çemberde herhangi bir θ açısı için:

📘 C. Trigonometrik Fonksiyonların Değer Aralıkları

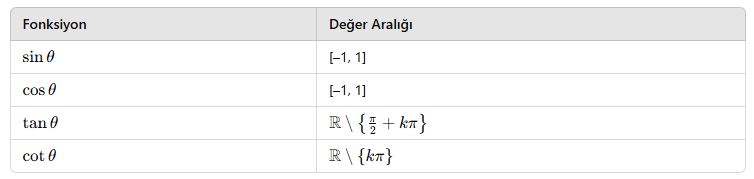
📘 D. Dört Bölge ve İşaretler

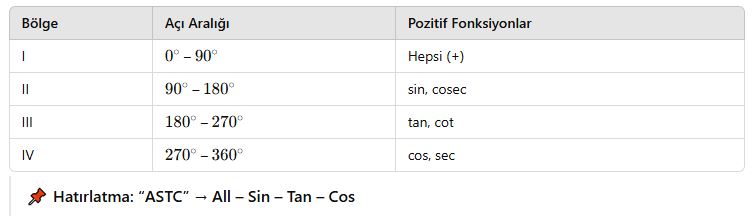
📘 E. Özel Açıların Birim Çember Üzerindeki Noktaları

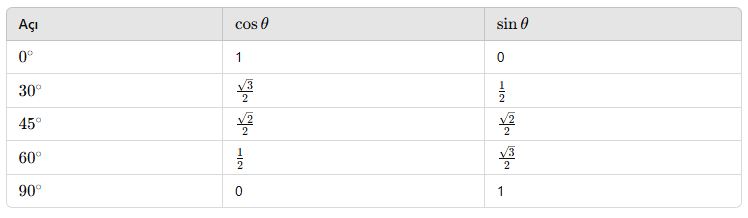
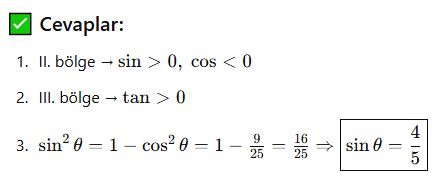
Trigonometrik Fonksiyonların Özellikleri ve Grafikler

A. Trigonometrik Fonksiyonların Özellikleri

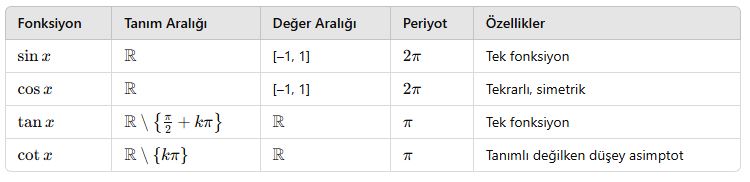
B. Fonksiyonların Parite Özellikleri

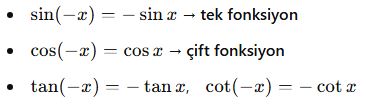
C. Fonksiyonların Grafik Özeti

D. Genelleştirilmiş Fonksiyonlar:

Trigonometrik Eşitlikler ve Özdeşlikler

📘 A. Temel Trigonometrik Özdeşlikler

1. Pisagor Özdeşlikleri

​

Diğer iki özdeşlik, bu temel bağıntıdan türetilir:

2. Tanım Özdeşlikleri

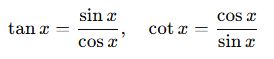
3. Ters Fonksiyon Özellikleri

📘 B. Açıların İşaret Özellikleri (Bölgeye Göre)

“ASTC” kuralı:

• I. bölge: Tüm fonksiyonlar pozitif

• II. bölge: Sinüs pozitif

• III. bölge: Tanjant pozitif

• IV. bölge: Kosinüs pozitif

📘 C. Türevsel Eşitlikler (Açı Tamamlayıcıları)

1. 90° Tamamlayıcılığı (Komplemaner Açı)

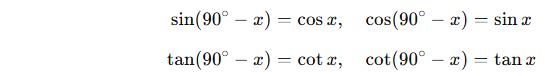
2. 180°-360° Dönüşümleri

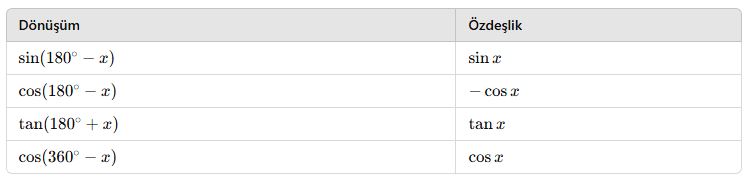
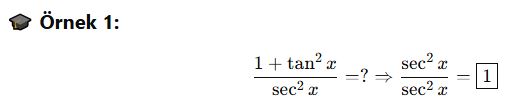
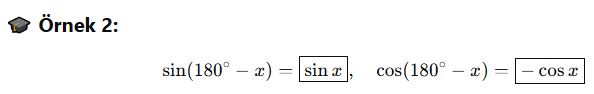
📌 Not:

Bu özdeşlikler çokça sadeleştirme, dönüştürme ve denklemlerde köprü görevi görür.

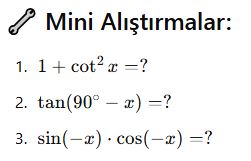
Açılarla İlgili Formüller (Toplam–Fark, 2 Katı, Yarım Açı)

📘 A. Toplam ve Fark Formülleri

Sinüs:

Kosinüs:

📌 Not: Kosinüste işaret ters çevrilir

Tanjant:

​

🎓 Örnek:

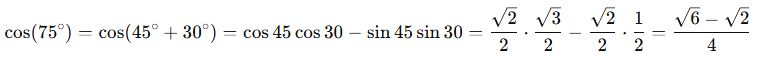
📘 B. 2 Kat Açı Formülleri

Sinüs:

Kosinüs:

Tanjant:

🎓 Örnek:

📘 C. Yarım Açı Formülleri

Türevleriyle birlikte yarım açı denklemlerinde kullanılır.

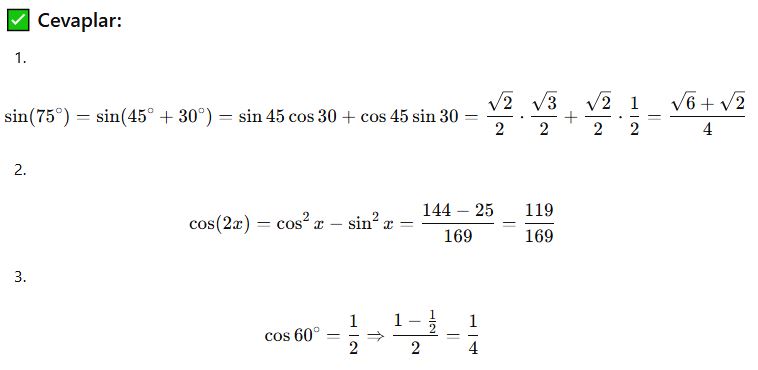
Trigonometrik Denklemler ve Çözüm Kümeleri

📘 A. Trigonometrik Denklemler Nedir?

Bir trigonometrik fonksiyonu içeren ve belirli açıları/aradaki ilişkiyi bulmayı amaçlayan denklemlerdir.

Genellikle:

• Verilen trigonometrik oranı sağlayan açılar bulunur

• Birim çember veya özel açı bilgisi kullanılır

• Çözüm, 0 ile 360° (veya 0 ≤ x < 2π) aralığında veya genel çözüm şeklinde istenir

📘 B. Temel Trigonometrik Eşitlikler

🔸 Örnek 1:

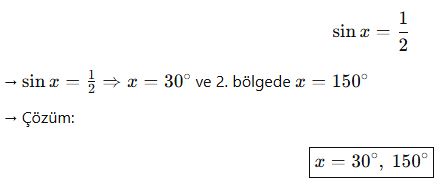
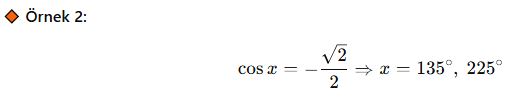
📘 C. Genel Çözüm Formları

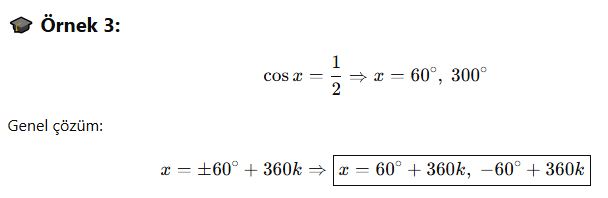
📘 D. Denklem Dönüştürme Gerekebilir

Bazı denklemler sadeleştirme veya özdeşlik uygulaması gerektirir:

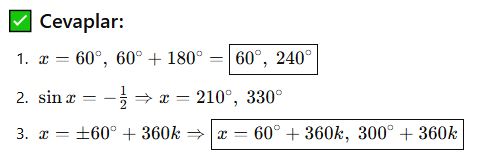
Trigonometri AYT Deneme Testi

(Cevap anahtarı en altta)