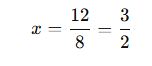TYT Matematik Denklem Çözme Konu Anlatımı

Birinci Dereceden Bir Bilinmeyenli Denklemler

Birinci dereceden bir bilinmeyenli denklemler, ax + b = 0 formunda yazılabilen denklemlerdir.
Burada:

• a ve b reel sayılar,
• x ise bilinmeyendir.

Örnekler ve Çözümler

Birinci Dereceden İki Bilinmeyenli Denklemler

Birinci dereceden iki bilinmeyenli denklemler ax + by = c formunda yazılabilir.
Bu tür denklemler tek başına çözülemez, bir başka denklemle birlikte çözülmesi gerekir.

Örnek Sistem:

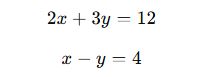
Bu sistemi çözmek için yerine koyma yöntemi veya yok etme yöntemi kullanabiliriz.

Yerine Koyma Yöntemi

Yerine koyma yöntemi, bir denklemde bir bilinmeyeni yalnız bırakıp, diğer denklemde yerine koyma işlemiyle çözme yöntemidir.

Örnek:

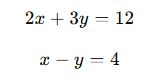
Adım 1: Bir değişken yalnız bırakılır.

İkinci denklemden x’i yalnız bırakıyoruz:

Adım 2: Bulduğumuz ifadeyi diğer denklemde yerine koyarız.

Adım 3: Çözüm yapılır.

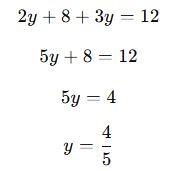
Adım 4: Bulunan değer yerine konur.

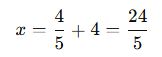
Çözüm Kümesi:

Yok Etme Yöntemi

Yok etme yöntemi, iki bilinmeyenli denklem sistemlerinde değişkenlerden birini yok ederek çözüm bulma yöntemidir.

Örnek:

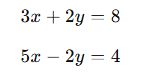
Adım 1: Denklemleri toplayarak bir bilinmeyeni yok etme.

2y ve -2y birbirini götürür:

Adım 2: x’i bulma.

​

Adım 3: Bulunan x değerini yerine koyma.

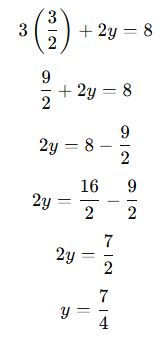
Çözüm Kümesi:

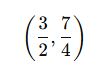
Çözüm Kümesi – Katsayı İlişkisi

Birinci dereceden iki bilinmeyenli denklemler grafikte doğrular ile ifade edilir.

1. Eğer iki doğru kesişiyorsa, tek bir çözüm vardır (Bağımsız sistem).
2. Eğer iki doğru çakışıyorsa, sonsuz çözüm vardır (Bağımlı sistem).
3. Eğer iki doğru paralelse, çözüm yoktur (Tutarsız sistem).

Örnek Çözüm Kümesi Problemi

Aşağıdaki denklem sisteminin kaç çözümü vardır?

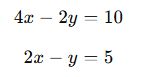
Katsayıları karşılaştıralım:

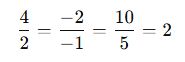
Sonuç:
Bu sistem sonsuz çözüm içerir. (Aynı doğrudur.)

Özet:

• Birinci Dereceden Bir Bilinmeyenli Denklemler: 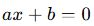 şeklindedir.
• Birinci Dereceden İki Bilinmeyenli Denklemler: 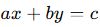 şeklindedir.
• Yerine Koyma Yöntemi: Bir değişken yalnız bırakılır ve diğer denklemde yerine konur.
• Yok Etme Yöntemi: Bir değişken yok edilerek diğer değişken bulunur.
• Çözüm Kümesi ve Katsayı İlişkisi:
  • Kesiyorsa → Tek çözüm
  • Çakışıyorsa → Sonsuz çözüm
  • Paralelse → Çözüm yok

TYT Matematik: Denklem Çözme Testi

Birinci Dereceden Bir Bilinmeyenli Denklemler

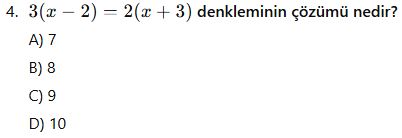
Birinci Dereceden İki Bilinmeyenli Denklemler

Yerine Koyma Yöntemi

Yok Etme Yöntemi

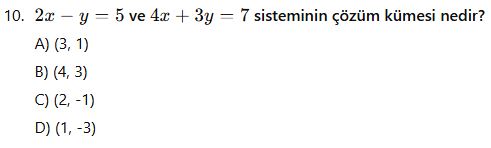
Çözüm Kümesi ve Katsayı İlişkisi

Denklem Problemleri

Denklem Çözme ile İlgili Karışık Sorular

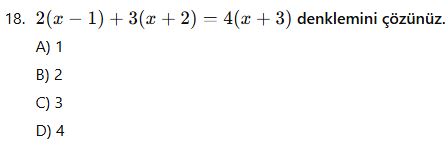
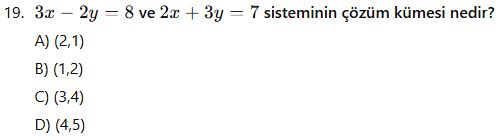
Cevap Anahtarı

1. C
2. A
3. B
4. D
5. A
6. C
7. B
8. A
9. A
10. C
11. B
12. B
13. A
14. C
15. C
16. D
17. C
18. B
19. A
20. C