TYT Matematik Mutlak Değer Konu Anlatımı

Mutlak değer, bir sayının sayı doğrusu üzerindeki sıfırdan uzaklığını ifade eder. Yani, mutlak değer her zaman pozitif veya sıfır olur. Mutlak değer kavramı, eşitsizlikler, denklemler ve çeşitli işlemlerde karşımıza çıkar. Bu ünitede, mutlak değerin tanımından başlayarak temel özellikleri, kuralları, çarpma ve bölme işlemleri ile mutlak değerli denklemler ve eşitsizliklerin nasıl çözüldüğünü örneklerle ele alacağız.

Mutlak Değerin Tanımı ve Özellikleri

• Tanım:
  Bir sayının mutlak değeri, o sayının sıfırdan olan uzaklığıdır.

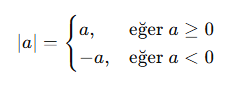
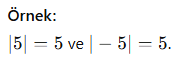
Mutlak Değerin Özellikleri

Mutlak Değerin Temel Kuralları

• Çarpma Kuralı:

• Bölme Kuralı:

• Toplama ve Çıkarma için Kurallar:
  Mutlak değerler, doğrudan toplama veya çıkarma işlemine girmeden önce ifadelerin işaretlerine dikkat edilmelidir.

Mutlak Değerin Pozitif Olma Kuralı

• Herhangi bir sayının mutlak değeri daima pozitif (veya sıfır) olmak zorundadır.
  Örneğin:

Çarpma ve Bölme İşlemlerinde Mutlak Değer

• Çarpma:

Örnek:

• Bölme:

Örnek:

Eşitsizlikler ve Mutlak Değer

• Mutlak Değerli İfade ile İlişkili Eşitsizlikler:

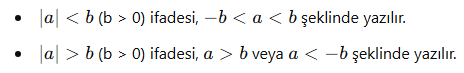
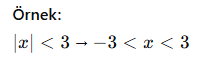
Mutlak Değerli Denklemler

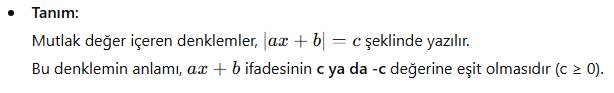
Mutlak Değerli Denklemler Nasıl Çözülür?

• Adım Adım Çözüm:

Mutlak Değerli Eşitsizlikler

Mutlak Değerli Eşitsizlikler Nasıl Çözülür?

• Örnek:

TYT Matematik – Mutlak Değer Ünitesi Testi

Aşağıdaki test, Mutlak Değer konusunu pekiştirmenize yardımcı olacaktır. Soruları dikkatlice okuyup en doğru seçeneği işaretleyin.

1. | -7 | işleminin sonucu kaçtır?

A) -7
B) 0
C) 7
D) -1

2. |5 – 8| işleminin sonucu kaçtır?

A) -3
B) 3
C) 13
D) -13

3. |x| = 9 denkleminin çözüm kümesi nedir?

A) {9}
B) {-9}
C) {-9, 9}
D) {0}

4. Aşağıdaki ifadelerden hangisi doğrudur?

A) |a| her zaman negatif bir sayıdır.
B) |a| ≥ 0’dır.
C) |a| ≤ 0’dır.
D) |a| < 0’dır.

5. |x – 4| = 2 denklemini sağlayan x değerleri kaçtır?

A) x = 2
B) x = 6
C) x = 2 ve x = 6
D) x = -2 ve x = -6

6. |x + 3| < 5 eşitsizliğinin çözüm kümesi nedir?

A) -8 < x < 2
B) -5 < x < 5
C) -2 < x < 8
D) -8 < x < 2

7. |2x – 1| = 7 denkleminin çözüm kümesi nedir?

A) {4, -3}
B) {3, -4}
C) {4, 3}
D) {7, -7}

8. Aşağıdaki işlemlerden hangisinin sonucu doğrudur?

A) |6 – 9| = -3
B) |4 × (-2)| = 8
C) |7 + (-3)| = -4
D) |-15| = -15

9. |x – 2| ≥ 5 eşitsizliğinin çözüm kümesi nedir?

A) x ≤ -3 veya x ≥ 7
B) x ≥ -3 veya x ≤ 7
C) -3 < x < 7
D) x > -3 ve x < 7

10. |3x + 1| ≤ 5 eşitsizliğinin çözüm kümesi nedir?

A) -6 ≤ x ≤ 4
B) -2 ≤ x ≤ 1
C) -5 ≤ x ≤ 3
D) -3 ≤ x ≤ 2

Cevap Anahtarı

1. C
2. B
3. C
4. B
5. C
6. D
7. A
8. B
9. A
10. B

Bu testi çözüp kendinizi değerlendirebilirsiniz. Hatalı olduğunuz soruları tekrar gözden geçirmeyi unutmayın! 🚀📚