TYT Matematik Olasılık Konu Anlatımı

Olasılık, bir olayın gerçekleşme ihtimalini inceleyen matematik dalıdır. Günlük hayatta hava durumu tahminleri, şans oyunları, istatistik analizleri ve karar verme süreçlerinde sıkça kullanılır.

Bu ünitede, temel olasılık kavramlarını ele alacak ve olaylarla işlemler, olasılık hesaplamaları ve problem çözme teknikleri üzerinde duracağız. 🚀

1. Olasılık Kavramları

Olasılıkla ilgili temel kavramları anlamak için önce temel terimleri öğrenmemiz gerekir.

📌 Deney (Deneysel Olay):
Bir olayın sonucunu görmek için yapılan tekrarlanabilir işlem.
📌 Örnek Uzay (S):
Bir deneyde meydana gelebilecek tüm olası sonuçların kümesi.
📌 Olay (A):
Örnek uzayın alt kümesi, yani deney sonucunda meydana gelebilecek belirli bir durum.
📌 Olasılık (P(A)):
Bir olayın gerçekleşme ihtimali,     aralığında bir değerdir.

Örnek 1: Örnek Uzay ve Olaylar

📌 Soru:
Bir zar atıldığında, örnek uzay ve bazı olayları belirleyelim.

📌 Çözüm:
Örnek uzay:

S={1,2,3,4,5,6}

Bazı olaylar:

• Tek sayı gelmesi: A={1,3,5}
• Çift sayı gelmesi: B={2,4,6}
• 5 veya 6 gelmesi: C={5,6}

✅ Sonuç: Olasılığı hesaplamak için bu olayların kaç elemanlı olduğuna bakacağız.

2. Olaylarla İşlemler

Bir deneyde meydana gelebilecek farklı olaylar arasında çeşitli işlemler yapılabilir. Olasılık teorisinde, birleşim, kesişim ve tamamlayıcı olaylar gibi işlemler sıkça kullanılır.

1. Birleşim (A ∪ B) – “Veya” Kuralı

İki veya daha fazla olayın en az birinin gerçekleştiği durumu ifade eder.

📌 Formül:

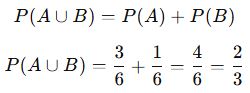
✅ Sonuç: Tek sayı veya 4 gelme olasılığı 2/3​‘tür.

2. Kesişim (A ∩ B) – “Ve” Kuralı

İki olayın aynı anda gerçekleştiği durumu ifade eder.

📌 Formül:

📌 Örnek 2:
Bir desteden rastgele çekilen kartın kırmızı ve kupa olma olasılığı nedir?

📌 Çözüm:

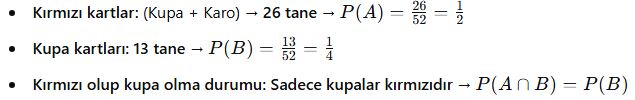
3. Tamamlayıcı Olay (A’)

Bir olayın gerçekleşmemesi durumudur.

📌 Formül:

📌 Örnek 3:
Bir zar atıldığında “5 veya 6 gelmeme” olasılığı nedir?

📌 Çözüm:

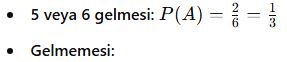
4. Ayrık (Bağımsız) ve Ayrık Olmayan Olaylar

🔹 Ayrık olaylar: Ortak elemanı olmayan olaylardır. (Örn: “Tek sayı” ve “Çift sayı” gelmesi)
🔹 Ayrık olmayan olaylar: Ortak elemanı olan olaylardır.

📌 Örnek 4:
Bir kart çekildiğinde “as” veya “kupa” gelme olasılığı nedir?

📌 Çözüm:

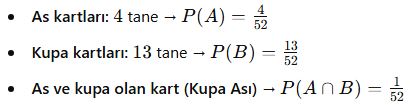
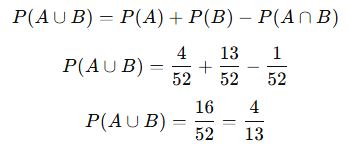
Özet Tablo

3. Olasılık Hesaplama

Bir olayın gerçekleşme olasılığı, olayla ilgili istenen durumların toplam duruma oranı olarak hesaplanır.

📌 Temel Olasılık Formülü:

1. Basit Olasılık Hesaplama

📌 Örnek 1:
Bir madeni para atıldığında yazı gelme olasılığı nedir?

📌 Çözüm:

2. Zar Atma Olasılığı

📌 Örnek 2:
Bir zar atıldığında çift sayı gelme olasılığı nedir?

📌 Çözüm:

3. Deste Kartları Olasılığı

📌 Örnek 3:
Bir iskambil destesinde rastgele çekilen kartın maça olma olasılığı nedir?

📌 Çözüm:

• Toplam kart sayısı: 52
• Maça kartları: 13 tane

4. Olasılık Hesaplamalarında Özel Durumlar

📌 Örnek 4:
Bir torbada 4 kırmızı, 5 mavi ve 6 yeşil top bulunmaktadır. Rastgele çekilen topun mavi olma olasılığı nedir?

📌 Çözüm:

5. En Az veya En Fazla Olasılık Hesaplama

📌 Örnek 5:
Bir zar atıldığında en az 3 gelme olasılığı nedir?

📌 Çözüm:

Özet Tablo

4. Olasılık Problemleri

Olasılık problemlerinde, verilen bilgileri doğru analiz ederek uygun formülleri kullanmak gereklidir. Bu bölümde, farklı türde olasılık problemlerini inceleyerek pratik yapacağız

1. Basit Olasılık Problemleri

📌 Örnek 1:
Bir madeni para 3 kez atılıyor. 2 kez yazı gelme olasılığı nedir?

📌 Çözüm:

📌 Örnek 2:
Bir zar 2 kez atılıyor. Her iki atışta da çift sayı gelme olasılığı nedir?

📌 Çözüm:

2. Kart Çekme Olasılığı

📌 Örnek 3:
Bir iskambil destesinde rastgele bir kart çekildiğinde, kırmızı ve as olma olasılığı nedir?

📌 Çözüm:

• Kırmızı kartlar: 26
• As kartları: 4 (Bunların 2’si kırmızı)

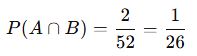
✅ Sonuç: Kırmızı ve as çekme olasılığı 1/26​‘dır.

3. En Az ve En Fazla Problemleri

📌 Örnek 4:
Bir zar 3 kez atılıyor. En az 1 kez 6 gelme olasılığı nedir?

📌 Çözüm:

• Önce “hiç 6 gelmemesi” durumunu bulalım:
• 6 dışındaki sayılar: {1,2,3,4,5} → 5 durum var
• Her atışta 6 gelmeme olasılığı:

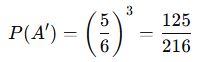
En az 1 kez 6 gelme olasılığı:

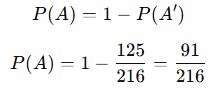
4. Birden Fazla Durumun Olasılığı

📌 Örnek 5:
Bir torbada 4 kırmızı, 5 mavi ve 3 sarı top vardır. Rastgele çekilen topun kırmızı veya sarı olma olasılığı nedir?

📌 Çözüm:

Özet Tablo

5. Sayma Yöntemleri ile Olasılık Problemleri

Olasılık hesaplamalarında, tüm olası durumları belirlemek için sayma yöntemleri kullanılır. Permütasyon, kombinasyon ve çarpma yöntemi, olasılık problemlerini çözmede sıkça kullanılır.

1. Çarpma Kuralı ile Olasılık

📌 Örnek 1:
Bir şifre 3 rakamdan oluşuyor ve her rakam 0-9 arasında seçiliyor. Şifrenin 123 olma olasılığı nedir?

📌 Çözüm:

• Toplam şifre kombinasyonları:

• İstenen şifre (123) sadece 1 tanedir.

2. Permütasyon ile Olasılık

📌 Örnek 2:
Bir yarışmada 8 kişi yarışıyor. İlk 3’e giren kişilerin sırası önemli olduğuna göre, belirli bir 3 kişinin ilk 3’e girmesi olasılığı nedir?

📌 Çözüm:

• Toplam sıralamalar:

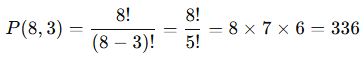
Belirli 3 kişi ilk 3’e girecekse, 3 kişi kendi içinde sıralanır:

Olasılık:

3. Kombinasyon ile Olasılık

📌 Örnek 3:
Bir torbada 6 kırmızı, 4 mavi top var. Rastgele 3 top çekildiğinde, 2 kırmızı 1 mavi gelme olasılığı nedir?

📌 Çözüm:

• Toplam durum:

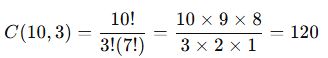
2 kırmızı ve 1 mavi seçme:

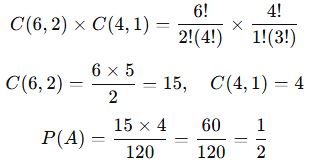
4. Sayılarla Olasılık Problemleri

📌 Örnek 4:
1,2,3,4,5 rakamlarıyla oluşturulan 3 basamaklı tek sayıların olasılığı nedir?

📌 Çözüm:

• Toplam 3 basamaklı sayılar:

Son rakamın tek olması için (1,3,5 seçilebilir)

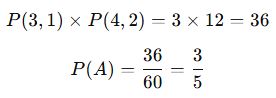
Özet Tablo

6. Koşullu Olasılık

Koşullu olasılık, bir olayın gerçekleştiği bilindiğinde başka bir olayın gerçekleşme olasılığı anlamına gelir. Ön bilgi kullanılarak olasılık daraltılır ve sadece ilgili durumlar dikkate alınır.

1. Koşullu Olasılık Formülü

Bir B olayının gerçekleştiği bilindiğinde, A olayının olasılığı şu formülle hesaplanır:

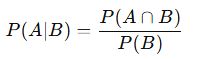
2. Koşullu Olasılık Problemleri

📌 Örnek 1:
Bir torbada 3 kırmızı, 4 mavi, 5 sarı top bulunmaktadır. Çekilen bir topun kırmızı olduğu bilindiğinde, mavi olma olasılığı nedir?

📌 Çözüm:

📌 Örnek 2:
Bir zar atılıyor. Gelen sayının çift olduğu bilindiğinde, 4 gelme olasılığı nedir?

📌 Çözüm:

📌 Örnek 3:
Bir kutuda 5 beyaz, 3 siyah, 2 mavi top var. Seçilen topun siyah olduğu bilindiğinde, tekrar çekilen topun mavi olma olasılığı nedir?

📌 Çözüm:

• Toplam top sayısı: 10
• İlk çekilen top siyahsa, geriye 9 top kalır.
• Mavi çekme olasılığı:

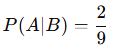
3. Bağımsız ve Bağımlı Olaylar

🔹 Bağımsız olaylar: İlk olayın sonucu, ikinci olayı etkilemez.

🔹 Bağımlı olaylar: İlk olay gerçekleştiğinde, ikinci olayın olasılığı değişir.

📌 Örnek 4:
Bir kutuda 4 kırmızı, 5 mavi, 3 beyaz top var. Peş peşe çekilen iki topun ikisinin de kırmızı olma olasılığı nedir?

📌 Çözüm:

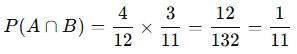
4. Özet Tablo

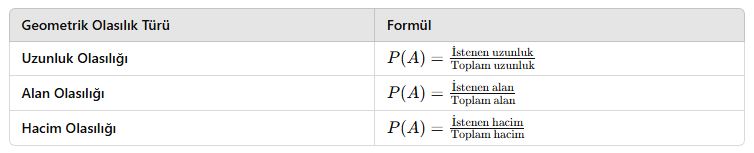
7. Geometrik Olasılık

Geometrik olasılık, alan, uzunluk veya hacim üzerinden yapılan olasılık hesaplamalarıdır. Klasik olasılıktan farkı, diskret (ayrık) yerine sürekli (kesintisiz) olaylarla çalışmasıdır.

📌 Geometrik Olasılık Formülü:

Burada:

• Ölçü, uzunluk, alan veya hacim olabilir.
• İstenen bölge, belirli bir şartı sağlayan kısmı ifade eder.

1. Uzunluk Üzerinden Geometrik Olasılık

📌 Örnek 1:
0 ile 10 arasındaki sayılardan rastgele seçilen bir sayının 4 ile 7 arasında olma olasılığı nedir?

📌 Çözüm:

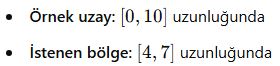
2. Alan Üzerinden Geometrik Olasılık

📌 Örnek 2:
Bir kare içinde rastgele seçilen bir noktanın, belirli bir bölgeye düşme olasılığı nedir?

📌 Verilenler:

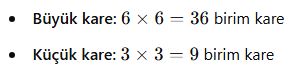
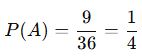
3. Çember ve Daire Üzerinde Geometrik Olasılık

📌 Örnek 3:
Bir çember içinde rastgele seçilen bir noktanın, iç içe geçmiş bir küçük çemberde olma olasılığı nedir?

📌 Verilenler:

4. Hacim Üzerinden Geometrik Olasılık

📌 Örnek 4:
Bir küp içine rastgele atılan bir noktanın, içinde yer alan küçük bir küp içine düşme olasılığı nedir?

📌 Verilenler:

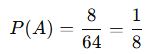
5. Geometrik Olasılığın Kullanım Alanları

📌 Gerçek hayat uygulamaları:

• Hedef oyunlarında isabet oranları
• Meteorolojide yağmur ihtimalleri
• Makine parçalarının üretim hataları
• Güvenlik sistemlerinde sensör alanları

6. Özet Tablo

TYT Matematik: Olasılık Konu Testi

Aşağıdaki soruları çözüp cevaplarınızı kontrol edebilirsiniz. 🚀

1. Temel Olasılık Soruları

Soru 1:

Bir torbada 3 kırmızı, 4 mavi ve 5 yeşil top vardır. Rastgele çekilen topun kırmızı olma olasılığı nedir?

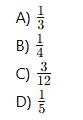
Soru 2:

Bir zar atıldığında asal sayı gelme olasılığı nedir?

Soru 3:

Bir iskambil destesinde rastgele çekilen bir kartın karo veya as olma olasılığı nedir?

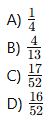
2. Koşullu Olasılık Soruları

Soru 4:

Bir torbada 6 kırmızı, 5 mavi, 4 yeşil top var. İlk çekilen topun kırmızı olduğu bilindiğinde, ikinci çekilen topun da kırmızı olma olasılığı nedir?

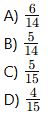
Soru 5:

Bir kutuda 7 siyah, 3 beyaz, 5 kırmızı top var. Çekilen topun siyah olduğu bilindiğinde, ikinci çekilen topun da siyah olma olasılığı nedir?

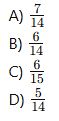
3. Geometrik Olasılık Soruları

Soru 6:

0 ile 20 arasında rastgele seçilen bir sayının 5 ile 10 arasında olma olasılığı nedir?

Soru 7:

10 cm çapında bir daire içinde, yarıçapı 3 cm olan bir çemberin içine düşme olasılığı nedir?

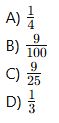
Soru 8:

Bir küp içine rastgele bırakılan bir noktanın, içinde yer alan yarı hacimli küçük küpe düşme olasılığı nedir?

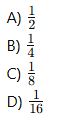
Cevap Anahtarı 📌

📚 Bu test, Olasılık konusunu pekiştirmenize yardımcı olacak! 🚀 Yanıtlarınızı kontrol edin ve eksiklerinizi tamamlayın! 🎯