6.Sınıf Matematik Çarpanlar ve Katlar Konu Anlatımı

Matematikte çarpanlar ve katlar, sayıların bölünebilme özelliklerini, ortak çarpanlarını ve asal sayıların önemini anlamamıza yardımcı olan temel kavramlardır. Günlük hayatta zaman planlaması, inşaat mühendisliği, kesirlerle işlem yapma, paketleme işlemleri ve veri analizi gibi birçok alanda çarpanlar ve katlar kullanılır.

Bu ünitede şunları öğreneceğiz:
✅ Bir sayının çarpanlarını ve katlarını nasıl belirleyeceğimizi,
✅ Bölünebilme kurallarını kullanarak sayıların hangi sayılara tam bölünebildiğini,
✅ Asal sayıların ne olduğunu ve nasıl belirlendiğini,
✅ Asal çarpanlara ayırma yöntemlerini,
✅ İki sayının ortak bölenlerini ve ortak katlarını nasıl bulacağımızı ve bu bilgileri problem çözümünde nasıl kullanacağımızı.

Doğal Sayıların Çarpanlarını ve Katlarını Belirleme

Matematikte bir sayının çarpanları ve katları, sayıların bölünebilirliği ve sayıların birbirleriyle olan ilişkilerini anlamamıza yardımcı olur. Bu kavramlar, ileride bölünebilme kuralları, asal çarpanlar, EBOB ve EKOK hesaplamaları gibi konuları anlamak için temel oluşturur.

Çarpan (Bölen) Nedir?

Bir sayıyı tam bölen doğal sayılara o sayının çarpanları (bölenleri) denir.

Çarpanları Bulma Yöntemi:

Bir sayının çarpanlarını bulmak için:
✔ Sayıyı hangi sayılarla çarparsak o sayıyı elde ederiz, bunları belirleriz.
✔ Çarpma işlemiyle yazılan sayılar, çarpanlar olarak adlandırılır.

✅ Örnek 1: 18 sayısının çarpanlarını bulalım.
18’i bölebilen sayıları belirleyelim:

Bu durumda 18’in çarpanları: 1, 2, 3, 6, 9 ve 18’dir.

✅ Örnek 2: 24 sayısının çarpanlarını bulalım.

24’ün çarpanları: 1, 2, 3, 4, 6, 8, 12 ve 24’tür.

Kat Nedir?

Bir sayının belirli bir çarpan ile çarpılarak elde edilen sonuçlarına o sayının katları denir.

Katları Bulma Yöntemi:

✔ Bir doğal sayının katlarını bulmak için, o sayıyı 1, 2, 3, 4, … gibi sayılarla çarparız.
✔ Katlar sonsuzdur çünkü bir sayının sonsuz tane katı olabilir.

✅ Örnek 3: 5 sayısının ilk 5 katını bulalım.

5 sayısının ilk 5 katı: 5, 10, 15, 20, 25’tir.

✅ Örnek 4: 8 sayısının ilk 4 katını bulalım.

8 sayısının ilk 4 katı: 8, 16, 24, 32’dir.

Çarpanlar ve Katlar Arasındaki Farklar

Örnek Sorular ve Çözümleri

✅ Soru 1: 36 sayısının çarpanlarını bulunuz.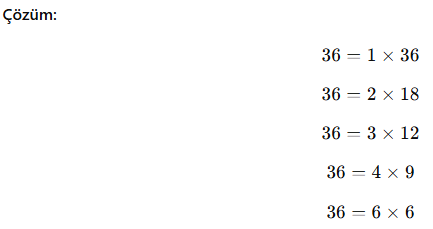

Çarpanları: 1, 2, 3, 4, 6, 9, 12, 18 ve 36.

✅ Soru 2: 7 sayısının ilk 5 katını bulunuz.

Cevap: 7, 14, 21, 28, 35.

✅ Soru 3: Bir sayının çarpanları 1, 2, 3, 6 ise bu sayı kaçtır?
Çözüm:
Bu sayı, çarpanları verilen en küçük sayıdır. Sayıyı oluşturan çarpanların en büyüğü 6 olduğu için cevap 6’dır.

Bölünebilme Kuralları

Bir sayının belirli bir sayıya tam bölünüp bölünmediğini anlamanın kolay yolları vardır. Bu kurallara bölünebilme kuralları denir. Bölünebilme kuralları sayesinde işlemlerimizi hızlandırabilir ve büyük sayılarla daha kolay çalışabiliriz.

Bu bölümde 2, 3, 4, 5, 6, 9 ve 10’a bölünebilme kurallarını öğreneceğiz.

2 ile Bölünebilme Kuralı

Kural: Bir sayı son rakamı (birler basamağı) 0, 2, 4, 6 veya 8 ise 2’ye tam bölünür.

✅ Örnekler:
✔ 38 → Son rakamı 8, bu yüzden 2’ye tam bölünür.
✔ 124 → Son rakamı 4, bu yüzden 2’ye tam bölünür.
❌ 157 → Son rakamı 7, bu yüzden 2’ye tam bölünmez.

3 ile Bölünebilme Kuralı

Kural: Bir sayının rakamları toplamı 3’ün katı ise o sayı 3’e tam bölünür.

✅ Örnekler:
✔ 123 → Rakamları toplamı: 1 + 2 + 3 = 6 (3’ün katı) → Bölünür.
✔ 255 → Rakamları toplamı: 2 + 5 + 5 = 12 (3’ün katı) → Bölünür.
❌ 428 → Rakamları toplamı: 4 + 2 + 8 = 14 (3’ün katı değil) → Bölünmez.

4 ile Bölünebilme Kuralı

Kural: Bir sayının son iki basamağı (birler ve onlar basamağı) 4’ün katı ise o sayı 4’e tam bölünür.

✅ Örnekler:
✔ 1.216 → Son iki basamak 16 (4’e bölünür) → Bölünür.
✔ 524 → Son iki basamak 24 (4’e bölünür) → Bölünür.
❌ 738 → Son iki basamak 38 (4’e bölünmez) → Bölünmez.

5 ile Bölünebilme Kuralı

Kural: Bir sayı sonu 0 veya 5 ile bitiyorsa 5’e tam bölünür.

✅ Örnekler:
✔ 75 → Son rakamı 5, bölünür.
✔ 120 → Son rakamı 0, bölünür.
❌ 83 → Son rakamı 3, bölünmez.

6 ile Bölünebilme Kuralı

Kural: Bir sayı hem 2’ye hem de 3’e tam bölünebiliyorsa 6’ya da tam bölünür.

✅ Örnekler:
✔ 144 → 2’ye bölünür (sonu 4) ve 3’e bölünür (1+4+4=9 → 3’ün katı) → Bölünür.
✔ 72 → 2’ye bölünür (sonu 2) ve 3’e bölünür (7+2=9) → Bölünür.
❌ 35 → 2’ye bölünmez (son rakamı 5) → Bölünmez.

9 ile Bölünebilme Kuralı

Kural: Bir sayının rakamları toplamı 9’un katı ise o sayı 9’a tam bölünür.

✅ Örnekler:
✔ 729 → Rakamları toplamı 7 + 2 + 9 = 18 (9’un katı) → Bölünür.
✔ 243 → Rakamları toplamı 2 + 4 + 3 = 9 (9’un katı) → Bölünür.
❌ 128 → Rakamları toplamı 1 + 2 + 8 = 11 (9’un katı değil) → Bölünmez.

10 ile Bölünebilme Kuralı

Kural: Bir sayı son rakamı 0 ise 10’a tam bölünür.

✅ Örnekler:
✔ 150 → Sonu 0 ile bitiyor → Bölünür.
✔ 4.320 → Sonu 0 ile bitiyor → Bölünür.
❌ 479 → Sonu 0 değil → Bölünmez.

Bölünebilme Örnek Sorular ve Çözümleri

✅ Soru 1: Aşağıdaki sayılardan hangisi 2’ye tam bölünmez?
A) 126
B) 418
C) 375
D) 200

Çözüm:

• 126 → Sonu 6 ile bittiği için 2’ye bölünür.
• 418 → Sonu 8 ile bittiği için 2’ye bölünür.
• 375 → Sonu 5 ile bittiği için 2’ye bölünmez.
• 200 → Sonu 0 ile bittiği için 2’ye bölünür.

Cevap: C) 375

✅ Soru 2: Aşağıdaki sayılardan hangisi 9’a tam bölünür?
A) 625
B) 972
C) 314
D) 185

Çözüm:

• 625 → 6+2+5 = 13 (9’un katı değil) → Bölünmez.
• 972 → 9+7+2 = 18 (9’un katı) → Bölünür.
• 314 → 3+1+4 = 8 (9’un katı değil) → Bölünmez.
• 185 → 1+8+5 = 14 (9’un katı değil) → Bölünmez.

Cevap: B) 972

Asal Sayılar ve Özellikleri

Matematikte bazı sayılar yalnızca 1 ve kendisine bölünebilir. Bu sayılara asal sayılar denir. Asal sayılar, matematiğin temel taşlarından biridir ve şifreleme sistemleri, bilgisayar bilimi, veri güvenliği gibi birçok alanda kullanılır.

Asal Sayı Nedir?

Asal sayı, sadece 1 ve kendisine bölünebilen 1’den büyük doğal sayılardır.

✅ Örnek Asal Sayılar:

Asal Olmayan (Bileşik) Sayılar

1 ve kendisinden başka en az bir böleni daha olan sayılara bileşik sayılar denir.

✅ Örnek Bileşik Sayılar:

✔ 4 → $1,2,4$ (Asal değil, çünkü 2’ye de bölünüyor)
✔ 9 → $1,3,9$ (Asal değil, çünkü 3’e de bölünüyor)

1 Sayısı Asal mı?

Hayır! Çünkü asal sayı 1’den büyük olmak zorundadır. 1’in yalnızca kendisi vardır, bu yüzden asal sayı değildir.

2 Neden Tek Çift Asal Sayıdır?

2 asal bir sayıdır çünkü yalnızca 1 ve kendisine bölünebilir. Ayrıca tek çift asal sayıdır, çünkü diğer tüm çift sayılar en az 2’ye bölünebilir ve bu yüzden asal olamaz.

100’e Kadar Olan Asal Sayılar

Bir Sayının Asal Olduğu Nasıl Anlaşılır?

Bir sayının asal olup olmadığını anlamak için şu yöntemi kullanabiliriz:

✔ Öncelikle sayının 2’ye, 3’e, 5’e veya 7’ye bölünüp bölünmediğini kontrol ederiz.
✔ Eğer bölünmüyorsa, sayı asaldır.

✅ Örnek 1: 47 sayısı asal mı?
✔ 47, 2’ye bölünmez (çift değil).
✔ 47, 3’e bölünmez (4+7 = 11, 3’e bölünmez).
✔ 47, 5’e bölünmez (son rakamı 0 veya 5 değil).
✔ 47, 7’ye bölünmez (47 ÷ 7 = tam bölünmez).
Sonuç: 47 bir asal sayıdır.

✅ Örnek 2: 51 sayısı asal mı?
✔ 51, 2’ye bölünmez (çift değil).
✔ 51, 3’e bölünür (5+1 = 6, 3’e tam bölünüyor).
Sonuç: 51 asal değildir.

Asal Sayılar Örnek Sorular ve Çözümleri

✅ Soru 1: Aşağıdaki sayılardan hangisi asaldır?
A) 15
B) 23
C) 27
D) 49

✅ Soru 2: Aşağıdaki sayıların hangisi asal değildir?
A) 11
B) 37
C) 51
D) 29

Doğal Sayıların Asal Çarpanlarını Belirleme

Bir doğal sayıyı sadece asal sayıların çarpımı şeklinde yazmaya asal çarpanlarına ayırma denir. Bu yöntem, özellikle EBOB (En Büyük Ortak Bölen) ve EKOK (En Küçük Ortak Kat) hesaplamalarında kullanılır.

Asal Çarpan Nedir?

Bir sayıyı yalnızca asal sayıların çarpımı şeklinde ifade etmek için o sayının asal çarpanlarını buluruz.

✅ Örnek:
30 sayısını asal çarpanlarına ayıralım.
30’u bölebilen en küçük asal sayı 2’dir.

Asal Çarpanlara Ayırma Yöntemi

Bir sayıyı asal çarpanlarına ayırmak için şu adımları takip ederiz:

✔ Adım 1: Sayıyı en küçük asal sayıya bölerek başlarız.
✔ Adım 2: Bölme işlemi kalana kadar devam eder.
✔ Adım 3: Sonuç, asal sayıların çarpımı şeklinde yazılır.

Örneklerle Asal Çarpan Bulma

✅ Örnek 1: 36 sayısını asal çarpanlarına ayıralım.
En küçük asal sayı 2 ile başlayalım:

✅ Örnek 2: 72 sayısını asal çarpanlarına ayıralım.

Asal Çarpan Ağacı Yöntemi

Bir sayının asal çarpanlarını ağaç yöntemi ile de bulabiliriz.

✅ Örnek 3: 48 sayısını asal çarpanlarına ayırma (Ağaç Yöntemi)

Asal Çarpanlar Örnek Sorular ve Çözümleri

✅ Soru 1: 45 sayısının asal çarpanlarını bulun.
Çözüm:

✅ Soru 2: 84 sayısının asal çarpanlarını bulun.
Çözüm:

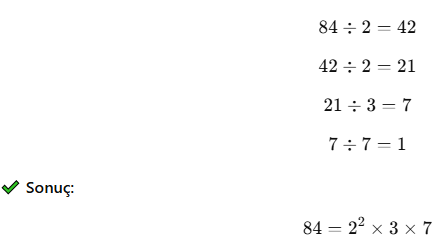
Ortak Bölenler ve Ortak Katlar

Matematikte bazı sayılar ortak çarpanlara ve ortak katlara sahiptir. İki veya daha fazla sayının ortak bölenlerini ve ortak katlarını belirlemek, EBOB (En Büyük Ortak Bölen) ve EKOK (En Küçük Ortak Kat) hesaplamalarında kullanılır.

Bu bölümde iki doğal sayının ortak bölenlerini ve ortak katlarını nasıl belirleyeceğimizi öğreneceğiz.

Ortak Bölen Nedir?

İki veya daha fazla sayıyı tam bölen sayılara ortak bölenler denir.

✅ Örnek: 12 ve 18’in ortak bölenlerini bulalım.

• 12’nin bölenleri: 1, 2, 3, 4, 6, 12
• 18’in bölenleri: 1, 2, 3, 6, 9, 18
• Ortak bölenler: 1, 2, 3, 6

En Büyük Ortak Bölen (EBOB)

İki sayının ortak bölenlerinden en büyüğüne EBOB (En Büyük Ortak Bölen) denir.

EBOB Bulma Yöntemi:

✔ Adım 1: Sayıların bölenlerini bulun.
✔ Adım 2: Ortak olanları belirleyin.
✔ Adım 3: En büyük olanını seçin.

✅ Örnek 1: 12 ve 18’in EBOB’unu bulalım.

• 12’nin bölenleri: 1, 2, 3, 4, 6, 12
• 18’in bölenleri: 1, 2, 3, 6, 9, 18
• Ortak bölenler: 1, 2, 3, 6
• EBOB = 6

✅ Örnek 2: 24 ve 36’nın EBOB’unu bulalım.

• 24’ün bölenleri: 1, 2, 3, 4, 6, 8, 12, 24
• 36’nın bölenleri: 1, 2, 3, 4, 6, 9, 12, 18, 36
• Ortak bölenler: 1, 2, 3, 4, 6, 12
• EBOB = 12

Ortak Kat Nedir?

İki veya daha fazla sayının ortak katları, her iki sayının da katı olan sayılardır.

✅ Örnek: 4 ve 6’nın ortak katlarını bulalım.

• 4’ün katları: 4, 8, 12, 16, 20, 24, 28, 32, …
• 6’nın katları: 6, 12, 18, 24, 30, 36, …
• Ortak katlar: 12, 24, 36, …

En Küçük Ortak Kat (EKOK)

İki sayının ortak katlarından en küçüğüne EKOK (En Küçük Ortak Kat) denir.

EKOK Bulma Yöntemi:

✔ Adım 1: Sayıların katlarını bulun.
✔ Adım 2: Ortak olanları belirleyin.
✔ Adım 3: En küçüğünü seçin.

✅ Örnek 1: 4 ve 6’nın EKOK’unu bulalım.

• 4’ün katları: 4, 8, 12, 16, 20, 24, …
• 6’nın katları: 6, 12, 18, 24, 30, …
• Ortak katlar: 12, 24, …
• EKOK = 12

✅ Örnek 2: 8 ve 12’nin EKOK’unu bulalım.

• 8’in katları: 8, 16, 24, 32, 40, 48, …
• 12’nin katları: 12, 24, 36, 48, 60, …
• Ortak katlar: 24, 48, …
• EKOK = 24

Asal Çarpanlara Ayırarak EBOB ve EKOK Bulma

EBOB ve EKOK’u bulmanın bir diğer yöntemi asal çarpanlara ayırma yöntemidir.

EBOB Bulma

✔ Sayıları asal çarpanlarına ayırın.
✔ Ortak olan asal çarpanların en küçük üslerini alın.

✅ Örnek: 36 ve 48’in EBOB’unu bulalım.

EKOK Bulma

✔ Sayıları asal çarpanlarına ayırın.
✔ Tüm asal çarpanların en büyük üslerini alın.

✅ Örnek: 36 ve 48’in EKOK’unu bulalım.

Ortak Bölenler ve Ortak Katlar Örnek Sorular ve Çözümleri

✅ Soru 1: 24 ve 36’nın EBOB’unu bulun.
Çözüm:

• 24’ün çarpanları: 1, 2, 3, 4, 6, 8, 12, 24
• 36’nın çarpanları: 1, 2, 3, 4, 6, 9, 12, 18, 36
• Ortak çarpanlar: 1, 2, 3, 4, 6, 12
• EBOB = 12

✅ Soru 2: 8 ve 12’nin EKOK’unu bulun.
Çözüm:

• 8’in katları: 8, 16, 24, 32, 40, 48, …
• 12’nin katları: 12, 24, 36, 48, …
• Ortak katlar: 24, 48, …
• EKOK = 24

Çarpanlar ve Katlar Ünitesi Değerlendirme Testi

1. Aşağıdaki sayılardan hangisinin çarpanları doğru verilmiştir?

A) 18 → 1, 2, 3, 6, 9, 18
B) 24 → 1, 2, 3, 4, 6, 12
C) 30 → 1, 2, 3, 5, 10, 30
D) 36 → 1, 2, 3, 4, 6, 9, 12, 18, 36

2. Aşağıdaki sayılardan hangisi asal sayıdır?

A) 21
B) 29
C) 35
D) 49

3. 2, 3, 4, 5, 6, 9 ve 10’a bölünebilme kurallarına göre, aşağıdaki sayılardan hangisi 3’e tam bölünebilir?

A) 412
B) 628
C) 735
D) 902

4. 81 sayısının asal çarpanları hangisidir?

A) 3 ve 9
B) 3
C) 3 ve 27
D) 1 ve 81

5. Aşağıdaki sayılardan hangisinin EBOB’u 6’dır?

A) 18 ve 24
B) 30 ve 42
C) 12 ve 18
D) 24 ve 36

6. 10 ve 15’in EKOK’u kaçtır?

A) 20
B) 30
C) 40
D) 50

7. Aşağıdaki sayılardan hangisinin 4 ile bölünebilme kuralına göre 4’e tam bölünür?

A) 728
B) 615
C) 342
D) 949

8. 20 ve 25’in en küçük ortak katı (EKOK) kaçtır?

A) 50
B) 60
C) 70
D) 80

9. 54 sayısının çarpanlarından hangisi yanlıştır?

A) 1
B) 3
C) 6
D) 10

10. Aşağıdaki ifadelerden hangisi yanlıştır?

A) 2, 3, 5 ve 7 asal sayıdır.
B) 9, asal bir sayıdır.
C) 10’un çarpanları 1, 2, 5 ve 10’dur.
D) 8 ve 12’nin EKOK’u 24’tür.

Cevap Anahtarı:

1. D
2. B
3. C
4. B
5. C
6. B
7. A
8. A
9. D
10. B