İçindekiler
Cebirsel İfadeler Konu Anlatımı
Matematikte, bilinmeyenleri ve değişkenleri temsil eden harflerle yapılan işlemlere cebirsel ifadeler denir. Cebirsel ifadeler, sayısal işlemleri genelleştirmek, desenleri belirlemek ve problemleri daha kolay çözmek için kullanılır.
Bu ünitede, cebirsel ifadelerde toplama ve çıkarma işlemleri, bir doğal sayı ile cebirsel ifadeyi çarpma işlemi ve sayı örüntüleri ile harfli ifadeler konularını öğreneceğiz.
Şimdi ilk konumuz olan “Cebirsel İfadelerde Toplama ve Çıkarma İşlemleri” ile başlayalım.
Cebirsel İfadelerde Toplama ve Çıkarma İşlemleri
Cebirsel ifadelerde toplama ve çıkarma işlemi yapılırken, benzer terimler bir araya getirilir.
✔ Benzer terimler, değişken kısmı aynı olan terimlerdir.
📌 Örnekler:
- 3x ve 5x benzer terimlerdir.
- 4a ve -2a benzer terimlerdir.
- 7y ve -3y benzer terimlerdir.
- 2x² ve -x² benzer terimlerdir.
Ancak, değişkenleri farklı olan terimler benzer terim değildir ve doğrudan toplanamaz.
📌 Örnek:
- 3x + 2y (Burada x ve y farklı değişkenler olduğu için toplanamaz.)
- 4a² + 3a (Burada a² ve a farklı değişken türleri olduğu için toplanamaz.)
1. Cebirsel İfadelerde Toplama İşlemi
Benzer terimler toplanırken kat sayılar toplanır, değişken kısmı aynı kalır.
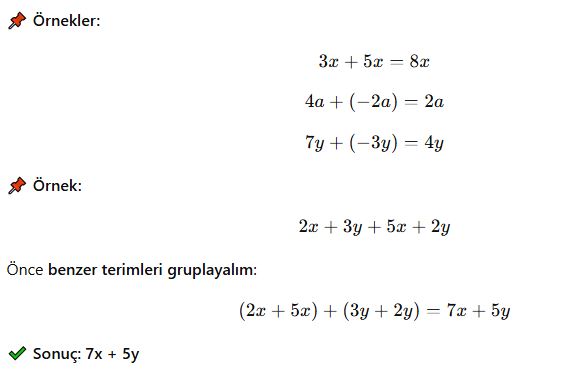
2. Cebirsel İfadelerde Çıkarma İşlemi
Çıkarma işlemi yapılırken, eksi işareti terimin tümüne uygulanır.


Bir Doğal Sayı ile Cebirsel İfadeyi Çarpma İşlemi
Cebirsel ifadelerle çarpma işlemi yapılırken, dağılma özelliği kullanılır. Bir doğal sayının cebirsel ifadeyle çarpılması, her terimin çarpanla ayrı ayrı çarpılması anlamına gelir.
1. Tek Terimli Cebirsel İfade ile Çarpma
Bir doğal sayı, tek terimli bir cebirsel ifade ile çarpılırken katsayılar çarpılır ve değişkenler olduğu gibi kalır.
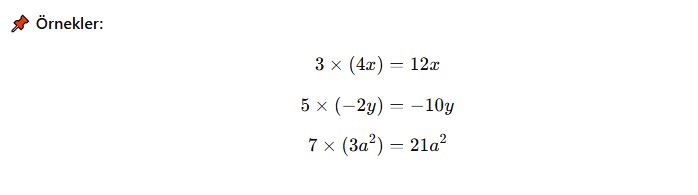
2. Çok Terimli Cebirsel İfade ile Çarpma (Dağılma Özelliği)
Eğer doğal sayı, birden fazla terim içeren bir cebirsel ifadeyle çarpılıyorsa, her terimle ayrı ayrı çarpılır.
✔ Bu işlem, dağılma özelliği olarak adlandırılır.
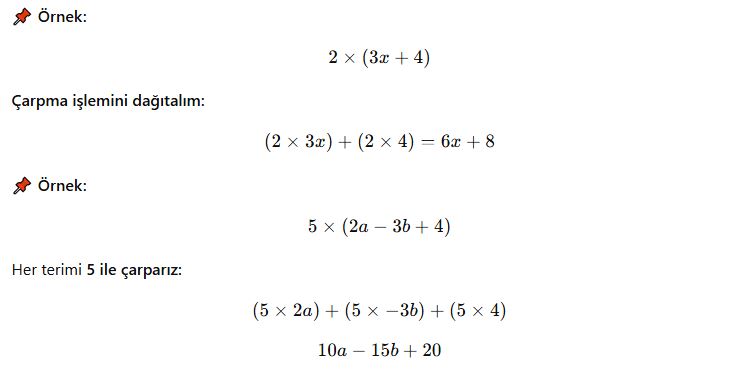
3. Cebirsel İfadelerin Parantez Dışına Alınması
Bazen cebirsel ifadeler çarpanlarına ayrılarak parantez dışına alınabilir.

Özet
✅ Tek terimli ifadelerle çarpma işlemi katsayıların çarpılmasıyla yapılır.
✅ Çok terimli ifadelerle çarpma yapılırken dağılma özelliği kullanılır.
✅ Bütün terimlerde ortak çarpan varsa, parantez dışına alınabilir.

Sayı Örüntüleri ve Harfli İfadeler
Matematikte sayı örüntüleri, belirli bir kurala göre devam eden sayı dizileridir. Bu örüntüler, aritmetik ve geometrik diziler, tekrarlayan desenler veya cebirsel ifadelerle ifade edilebilir.
Bu bölümde sayı örüntülerinin nasıl oluşturulduğunu, kuralının nasıl bulunacağını ve harfli ifadelerle nasıl gösterileceğini öğreneceğiz.
1. Sayı Örüntüleri Nedir?
Bir sayı örüntüsü, belli bir kurala göre sıralanmış sayılar dizisidir.
📌 Örnekler:
- 2, 4, 6, 8, 10, … → (Her terim bir önceki terime +2 eklenerek oluşur.)
- 3, 6, 9, 12, 15, … → (Her terim bir önceki terime +3 eklenerek oluşur.)
- 1, 2, 4, 8, 16, 32, … → (Her terim bir öncekinin 2 katı olarak devam eder.)
✔ Örüntünün kuralı bulunarak bilinmeyen terimler hesaplanabilir.
2. Sayı Örüntülerinin Cebirsel İfadelerle Gösterilmesi
Bir örüntünün genel kuralı, cebirsel bir ifade ile gösterilebilir. Eğer örüntüde bir düzen varsa, n. terimi belirleyen bir matematiksel ifade oluşturabiliriz.
📌 Örnek:
Örüntü: 3, 6, 9, 12, …
Her terim 3 ile çarpılıyor.
Genel kural: 3n
n = 1 için → 3×1 = 3
n = 2 için → 3×2 = 6
n = 3 için → 3×3 = 9
✔ Genel ifade: 3n
📌 Örnek:
Örüntü: 2, 5, 8, 11, 14, …
Bu dizide her terime 3 ekleniyor.
Genel kuralı belirleyelim:
✔ Genel ifade: 3n – 1
n = 1 için → 3×1 – 1 = 2
n = 2 için → 3×2 – 1 = 5
n = 3 için → 3×3 – 1 = 8
3. Harfli İfadelerle Örüntü Gösterimi
Bir sayı örüntüsü verildiğinde, harfli ifadelerle göstererek bilinmeyen değerleri bulabiliriz.
📌 Örnek:
Bir üçgenin çevresi, kenar uzunluğu a cm olan eşkenar üçgen için nasıl gösterilir?
✔ Çözüm:
Eşkenar üçgenin üç kenarı da aynı uzunluktadır, bu yüzden çevresi:
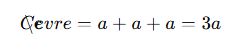
📌 Örnek:
Bir dikdörtgenin uzun kenarı x cm, kısa kenarı y cm. Dikdörtgenin çevresini cebirsel ifadeyle gösterelim.
✔ Çözüm:
Dikdörtgenin iki uzun ve iki kısa kenarı vardır.
![]()
4. Sayı Örüntülerinde Eksik Terimi Bulma
Bazen örüntülerde eksik terimi bulmamız gerekir.
📌 Örnek:
Örüntü: 5, 10, 15, 20, ? , 30
Eksik terim nedir?
✔ Çözüm:
Bu örüntü 5’er artmaktadır.
Eksik terim: 25
✔ Tam dizi: 5, 10, 15, 20, 25, 30
📌 Örnek Problemler:
- Aşağıdaki örüntünün kuralını bulun:
4, 7, 10, 13, 16, … - Aşağıdaki eksik terimi bulun:
2, 4, 8, ?, 32, 64 - Bir dikdörtgenin uzun kenarı 2x cm, kısa kenarı 3y cm ise çevreyi cebirsel ifadeyle gösteriniz.
- Bir karede kenar uzunluğu a cm ise, karenin çevresini cebirsel ifadeyle gösteriniz.
Cebirsel İfadeler – 10 Soruluk Test
1. Aşağıdaki cebirsel ifadelerden hangisi en sade haldedir?

2. Aşağıdaki işlemlerden hangisi doğrudur?
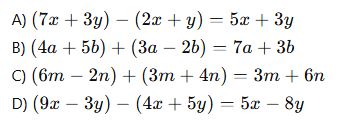

4. Bir dikdörtgenin uzun kenarı x cm, kısa kenarı y cm olduğuna göre çevresi nasıl gösterilir?

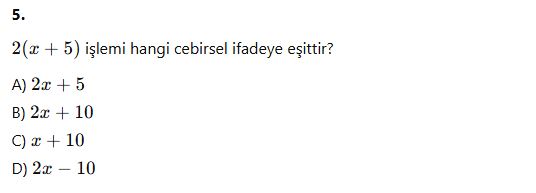
6. Bir kenarı a cm olan karenin çevresi nasıl gösterilir?

7. Aşağıdaki örüntü hangi kurala göre devam eder?
3, 6, 9, 12, 15, …


9. Bir kalemin fiyatı x TL, bir defterin fiyatı y TL ise 3 kalem ve 2 defterin toplam fiyatı nasıl gösterilir?

10. Aşağıdaki ifadelerden hangisi bir doğal sayı ile bir cebirsel ifadenin çarpımıdır?
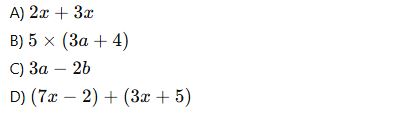
Cevap Anahtarı
1 – D
2 – B
3 – B
4 – B
5 – B
6 – A
7 – C
8 – C
9 – A
10 – B

