İçindekiler
Eşitlik ve Denklem Konu Anlatımı
Matematikte eşitlik ve denklemler, bilinmeyen değerleri bulmak için kullanılan temel kavramlardır. Denklemler, bir bilinmeyeni içeren matematiksel ifadeler olup, eşitlik kavramı üzerine kuruludur.
Bu ünitede, denklemde eşitliğin korunumu ilkesini öğrenecek, birinci dereceden bir bilinmeyenli denklemleri kuracak ve çözecek, gerçek hayat problemlerini denkleme çevirerek çözmeyi öğreneceğiz.
Şimdi ilk konumuz olan “Denklemlerde Eşitliğin Korunumu İlkesi” ile başlayalım.
Denklemlerde Eşitliğin Korunumu İlkesi
Bir eşitlik, iki matematiksel ifadenin birbirine eşit olduğunu gösterir.
Örneğin:
![]()
Bu ifadede sol taraf (3 + 5) ve sağ taraf (8) birbirine eşittir.
✔ Eşitliğin Korunumu İlkesi:
Bir eşitliğin her iki tarafına aynı sayı eklenirse, çıkarılırsa, çarpılırsa veya bölünürse, eşitlik bozulmaz.
📌 Örnekler:
Toplama:
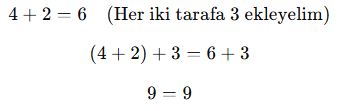
Eşitlik değişmedi.
Çıkarma:

Eşitlik değişmedi.
Çarpma:

Eşitlik değişmedi.
Bölme:

Eşitlik değişmedi.

Birinci Dereceden Bir Bilinmeyenli Denklemleri Kurma
Matematikte birinci dereceden bir bilinmeyenli denklemler, en fazla bir bilinmeyen içeren ve değişkenin üssü 1 olan denklemlerdir. Bu tür denklemler, günlük hayattaki birçok problemi matematiksel olarak modellememize yardımcı olur.
1. Birinci Dereceden Bir Bilinmeyenli Denklem Nedir?
Genel gösterimi:

Burada:
- x bilinmeyendir.
- a, b ve c birer sabit sayıdır.
- a ≠ 0 olmak zorundadır.
📌 Örnek Denklemler:
- 2x + 3 = 7
- 5x – 4 = 11
- x + 6 = 10
- 3x = 9
2. Günlük Hayatta Denklem Kurma
Bazı problemleri cebirsel denklemlerle ifade edebiliriz. Bunun için:
✅ Bilinmeyene bir harf verilir (genellikle x kullanılır).
✅ Problemin matematiksel ifadesi oluşturulur.
✅ Elde edilen denklem çözülerek bilinmeyen bulunur.
📌 Örnek:
Bir sınıftaki kız öğrencilerin sayısı, erkek öğrencilerin sayısından 5 fazladır. Erkek öğrenci sayısına x dersek, kız öğrencilerin sayısını nasıl ifade edebiliriz?
✔ Çözüm:
- Erkek öğrenci sayısı: x
- Kız öğrenci sayısı: x + 5
Denklem: Kız = x + 5
📌 Örnek:
Bir bakkalda satılan şekerin fiyatı x TL. 3 paket şeker alan bir müşteri 15 TL ödedi. Bu durumu matematiksel bir denklemle ifade edelim.
✔ Çözüm:
- 3 paket şekerin fiyatı: 3x
- Toplam ödeme: 15 TL
Denklem:
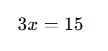
📌 Örnek:
Bir otobüste yolcu sayısı başlangıçta x kişidir. Daha sonra 12 kişi bindi ve toplam yolcu sayısı 40 oldu.
✔ Denklem:
![]()
3. Denklem Kurma Adımları
1️⃣ Bilinmeyeni belirle (x, y gibi harfler kullan).
2️⃣ Verilen bilgileri kullanarak matematiksel ifadeler oluştur.
3️⃣ Denklemi yaz ve sadeleştir.
4️⃣ Çözüm için bir sonraki adım olan denklemi çözme kısmına geç.
📌 Örnek Problemler:
- Bir öğrencinin yaşının 3 katı, 18’den 6 eksiktir. Bu durumu denklemle ifade ediniz.
- Bir çiftlikteki tavuk sayısı, koyun sayısının 2 katıdır. Eğer koyun sayısına x dersek, tavuk sayısını ifade eden denklemi yazınız.
- Bir markette bir şişe suyun fiyatı x TL. 5 şişe su alan bir müşteri toplamda 25 TL ödedi. Bu durumu denklemle ifade ediniz.
Birinci Dereceden Bir Bilinmeyenli Denklemlerin Çözümü
Birinci dereceden bir bilinmeyenli denklemler, en fazla bir bilinmeyen içeren ve değişkenin üssü 1 olan denklemlerdir. Bu tür denklemleri eşitliğin korunumu ilkesine uygun olarak çözüyoruz.
1. Denklem Çözme Adımları
Birinci dereceden bir bilinmeyenli denklemleri çözmek için şu adımları takip edebiliriz:
1️⃣ Bilinmeyen terimler (x içeren terimler) eşitliğin bir tarafına, sabit sayılar diğer tarafa alınır.
2️⃣ Gerekirse toplama, çıkarma, çarpma veya bölme işlemleri uygulanarak bilinmeyen yalnız bırakılır.
3️⃣ Sonuç sadeleştirilerek bilinmeyen bulunur.
2. Temel Denklem Çözme Örnekleri

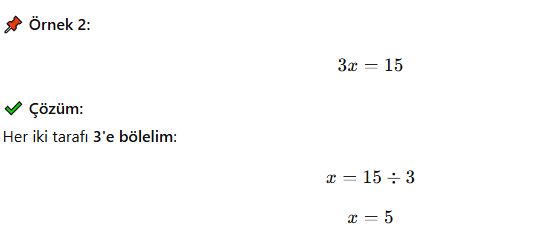


3. Parantezli ve Kesirli Denklemler


4. Denklem Çözmede Dikkat Edilmesi Gerekenler
✅ Toplama ve çıkarma işlemlerinde terimler yön değiştirirken işaretleri değişir.
✅ Çarpma ve bölme işlemleri yapılırken, bilinmeyen yalnız bırakılmalıdır.
✅ Kesirli denklemler çözülürken, paydadan kurtulmak için her iki tarafı aynı sayı ile çarpmak gerekir.
✅ Parantez varsa, önce dağılma özelliği uygulanmalıdır.

Birinci Dereceden Bir Bilinmeyenli Denklem Kurmayı Gerektiren Problemler
Matematikte günlük hayat problemlerini çözmek için denklemler kullanılır. Bir problemi denklemle çözmek için:
1️⃣ Bilinmeyen bir değişken seçilir (genellikle x kullanılır).
2️⃣ Problemin matematiksel modeli oluşturulur.
3️⃣ Kurulan denklem çözülerek bilinmeyen bulunur.
4️⃣ Sonuç yorumlanır ve kontrol edilir.
1. Günlük Hayatta Denklem Kullanımı
📌 Örnek 1: Yaş Problemi
Ali’nin yaşı, babasının yaşının 1/4’üne eşittir. Babasının yaşı x ise, Ali’nin yaşını bulmak için nasıl bir denklem kurarız?
✔ Çözüm:
- Babanın yaşı: x
- Ali’nin yaşı: x/4
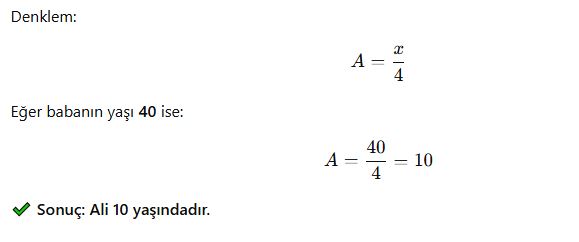
📌 Örnek 2: Alışveriş Problemi
Bir mağazada bir kazak x TL, bir pantolon ise 3 katı fiyatına satılmaktadır. Eğer toplam fiyat 400 TL ise, bu durumu denklemle ifade edelim ve kazağın fiyatını bulalım.
✔ Çözüm:
- Kazak fiyatı: x
- Pantolon fiyatı: 3x
- Toplam fiyat: x + 3x = 400

📌 Örnek 3: Mesafe Problemi
Bir otomobil, sabit bir hızla 3 saatte x km yol almıştır. Eğer 6 saatte toplam 360 km yol aldıysa, aracın hızını bulalım.
✔ Çözüm:
- 3 saatte gidilen yol: x
- 6 saatte gidilen yol: 2x = 360

2. Denklem Kurma Adımları Özet
✅ Bilinmeyen belirlenir (genellikle x kullanılır).
✅ Problemde verilenler matematiksel ifadelerle yazılır.
✅ Denklem oluşturulur ve çözülür.
✅ Sonuç yorumlanır.
📌 Örnek Problemler:
- Bir çiftlikte tavuk sayısı koyun sayısının 2 katıdır. Çiftlikte toplam 90 hayvan varsa, koyun sayısını bulun.
- Bir öğrenci, testin üçte birini çözdüğünde 12 soru tamamladı. Testte toplam kaç soru olduğunu bulun.
- Bir bakkal 3 kg elma ve 2 kg armut sattığında toplam 50 TL kazanıyor. Eğer elmanın kilosu x TL ve armutun kilosu 2x TL ise, elmanın kilogram fiyatını bulun.
- Bir otobüsteki yolcu sayısı, durakta 8 kişi binince 42 oldu. Başlangıçtaki yolcu sayısını bulun.
Eşitlik ve Denklem – 10 Soruluk Test
1.
Aşağıdaki ifadelerden hangisi eşitliğin korunumu ilkesine uygun bir işlemdir?
A) Eşitliğin bir tarafına 3 eklenirken diğer tarafına 5 eklenmesi
B) Eşitliğin her iki tarafına aynı sayının eklenmesi
C) Eşitliğin sadece sol tarafına 2 ile çarpma yapılması
D) Eşitliğin bir tarafına bölme, diğer tarafına toplama yapılması

3.
Bir mağazada bir gömleğin fiyatı x TL, bir pantolonun fiyatı ise 2x TL’dir. Eğer müşteri 1 gömlek ve 1 pantolon alıp 270 TL ödedi ise, bu durumu ifade eden denklem nedir?




7.
Bir otobüsteki yolcu sayısı x idi. Durakta 8 kişi binince toplam yolcu sayısı 42 oldu. Başlangıçtaki yolcu sayısını bulmak için kurulacak denklem nedir?

8.
Bir öğrencinin yaşı, babasının yaşının 1/5’ine eşittir. Babasının yaşı 50 ise öğrencinin yaşını veren denklem nedir?

9.
Bir çikolatanın fiyatı x TL ve bir dondurmanın fiyatı 3x TL’dir. 2 çikolata ve 1 dondurma alan bir müşteri 80 TL ödediğine göre, çikolatanın fiyatını bulmak için hangi denklem yazılmalıdır?
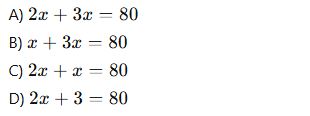
10.
Bir öğrencinin yaşı x, kardeşinin yaşı x – 3’tür. Eğer kardeşinin yaşı 10 ise öğrencinin yaşını veren denklem nedir?
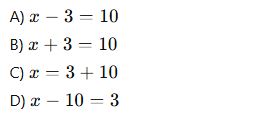
Cevap Anahtarı
1 – B
2 – B
3 – A
4 – B
5 – A
6 – B
7 – A
8 – D
9 – A
10 – A

