Rasyonel Sayılarla İşlemler Konu Anlatımı

Rasyonel sayılar, kesir biçiminde ifade edilebilen sayılardır ve toplama, çıkarma, çarpma, bölme gibi işlemlerle kullanılabilir. Bu ünitede, rasyonel sayılarla işlemler yapmayı öğrenecek, karesini ve küpünü hesaplamayı, çok adımlı işlemleri ve günlük hayatta karşılaşılan rasyonel sayı problemlerini çözeceğiz.

Şimdi ilk konumuz olan “Rasyonel Sayılarla Toplama ve Çıkarma İşlemleri” ile başlayalım.

Rasyonel Sayılarla Toplama ve Çıkarma İşlemleri

Rasyonel sayılarla toplama ve çıkarma işlemleri, kesirlerde toplama ve çıkarma işlemlerine benzer şekilde yapılır. İşlem yaparken şu adımları takip ederiz:

1. Paydaları Aynı Olan Rasyonel Sayılarla İşlemler

Eğer paydalar aynıysa, doğrudan payları toplayabilir veya çıkarabiliriz.

📌 Örnekler:

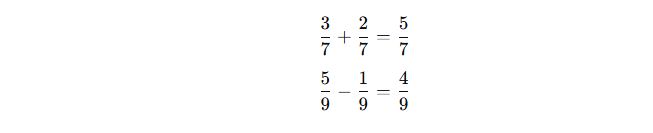
2. Paydaları Farklı Olan Rasyonel Sayılarla İşlemler

Eğer paydalar farklıysa, önce paydaları eşitleyerek toplama veya çıkarma işlemi yaparız.

📌 Örnek:

3. Rasyonel Sayılarla İşlem Kuralları

✅ Tam sayılar rasyonel sayı olarak yazılabilir:

• 4 = 4/1, -3 = -3/1

✅ Negatif rasyonel sayılar ile işlem yapılırken işaret kuralları unutulmamalıdır:

• (-3/4) + (1/4) = -2/4 = -1/2
• (-5/6) – (2/3) = -5/6 – 4/6 = -9/6 = -3/2

Rasyonel Sayılarla Çarpma ve Bölme İşlemleri

Rasyonel sayılarla çarpma ve bölme işlemleri, toplama ve çıkarmaya göre daha kolaydır. İşlem yaparken pay ve payda arasındaki ilişkileri kullanarak sadeleştirme yapılabilir. Şimdi rasyonel sayılarla çarpma ve bölme işlemlerini adım adım inceleyelim.

1. Rasyonel Sayılarla Çarpma İşlemi

Rasyonel sayılar çarpılırken:

• Paylar birbiriyle,
• Paydalar birbiriyle çarpılır.
• Sonuç sadeleştirilir.

📌 Örnekler:

2. Rasyonel Sayılarla Bölme İşlemi

Bölme işlemi çarpma işlemine dönüştürülerek yapılır:

Bölme işlemi yapılırken ikinci kesir ters çevrilir ve çarpma işlemi uygulanır.

Özet

✅ Çarpma işleminde paylar kendi arasında, paydalar kendi arasında çarpılır.
✅ Bölme işleminde ikinci kesir ters çevrilir ve çarpma işlemi yapılır.
✅ Sonuç sadeleştirilmelidir.

Rasyonel Sayıların Karesinin ve Küplerinin Hesaplanması

Bir sayının karesi veya küpü, o sayının kendisiyle belirli sayıda çarpılması anlamına gelir. Rasyonel sayılarda da aynı kural geçerlidir.

✔ Kare almak (İkinci kuvvet): Bir rasyonel sayıyı kendisiyle bir kez çarpmak demektir.
✔ Küp almak (Üçüncü kuvvet): Bir rasyonel sayıyı kendisiyle iki kez daha çarpmak demektir.

1. Rasyonel Sayıların Karesi (İkinci Kuvveti)

Bir rasyonel sayının karesi alınırken hem pay hem de payda ayrı ayrı karesine yükseltilir.

2. Rasyonel Sayıların Küpü (Üçüncü Kuvveti)

Bir rasyonel sayının küpü alınırken hem pay hem de payda ayrı ayrı küpüne yükseltilir.

Özet

✅ Bir rasyonel sayının karesi alınırken pay ve paydanın ayrı ayrı karesi alınır.
✅ Bir rasyonel sayının küpü alınırken pay ve paydanın ayrı ayrı küpü alınır.
✅ Negatif sayıların karesi pozitiftir.
✅ Negatif sayıların küpü negatiftir.

Rasyonel Sayılarla Çok Adımlı İşlemler

Rasyonel sayılarla işlem yaparken bazen toplama, çıkarma, çarpma ve bölme gibi işlemleri bir arada kullanmamız gerekebilir. Böyle durumlarda işlem sırasına dikkat etmeliyiz.

1. İşlem Önceliği Kuralları

Rasyonel sayılarla çok adımlı işlemleri yaparken aşağıdaki işlem sırasına dikkat edilmelidir:

1️⃣ Parantez içindeki işlemler önce yapılır.
2️⃣ Üslü işlemler varsa önce onlar yapılır.
3️⃣ Çarpma ve bölme işlemleri, soldan sağa doğru yapılır.
4️⃣ Toplama ve çıkarma işlemleri, soldan sağa doğru yapılır.

✔ İpucu: Paydaları eşitleme gerektiren işlemlerde önce paydalar eşitlenmelidir.

2. Örneklerle Çok Adımlı İşlemler

3. Çok Adımlı İşlemlerde İşlem Önceliği Özet

✅ Parantez içi işlemler önce yapılır.
✅ Çarpma ve bölme işlemleri toplama ve çıkarmadan önce yapılır.
✅ Paydalar eşitlenmeden toplama ve çıkarma işlemi yapılmaz.

Rasyonel Sayılarla İşlem Yapmayı Gerektiren Problemler

Günlük hayatta rasyonel sayılarla birçok işlem yaparız. Alışverişte indirim hesaplamaları, yemek tariflerinde ölçüler, yolculuklarda hız ve mesafe hesaplamaları gibi birçok durumda rasyonel sayılar kullanılır. Bu bölümde, rasyonel sayılarla işlem gerektiren problemlerin nasıl çözüleceğini öğreneceğiz.

1. Günlük Hayatta Rasyonel Sayılarla Problemler

📌 Örnek 1: Yemek Tarifi Problemi
Bir kek tarifinde 3/4 su bardağı süt kullanılmaktadır. Eğer bu tarifin 2 katı yapılmak istenirse kaç su bardağı süt gerekir?

✅ Çözüm:

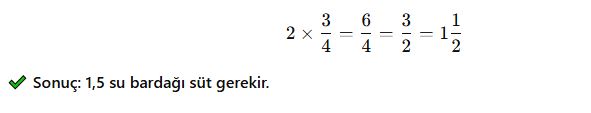
📌 Örnek 2: İndirim Hesaplama
Bir mağazada 120 TL’lik bir ürün %25 indirimle satılmaktadır. Ürünün indirimli fiyatı kaç TL olur?

2. Mesafe, Zaman ve Hız Problemleri

📌 Örnek 3: Yolculuk Problemi
Bir bisikletli, 2 saat boyunca saatte 3/4 km hızla gidiyor. Kaç kilometre yol alır?

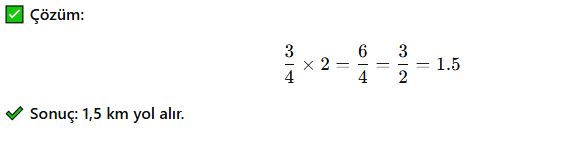
📌 Örnek 4: Paylaşma Problemi
Bir çiftlikte 35 litre süt, 7 kişiye eşit olarak dağıtılıyor. Her kişi kaç litre süt alır?

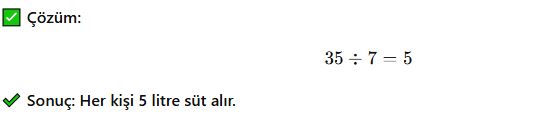
3. Rasyonel Sayılarla İşlem Problemleri

📌 Örnek 5: Karışım Problemi
Bir meyve suyu tarifinde 5/6 litre portakal suyu ve 2/3 litre elma suyu kullanılmaktadır. Toplam kaç litre meyve suyu elde edilir?

Özet

✅ Rasyonel sayılar günlük hayatta alışveriş, yemek tarifleri, hız hesaplamaları gibi birçok alanda kullanılır.
✅ Problemler çözülürken işlem önceliği ve payda eşitleme kurallarına dikkat edilmelidir.
✅ Kesirli işlemler sadeleştirilerek yapılmalıdır.

📌 Örnek Problemler:

1. Bir fırın, 3/4 kg unla bir ekmek yapıyor. Aynı fırın 5 ekmek yapmak için kaç kg un kullanır?
2. Bir tren, saatte 5/6 km hızla 4 saat yol aldı. Tren toplam kaç km yol almıştır?
3. Bir havuz, 1/2 saat içinde 3/8’lik kısmı doluyor. Havuzun tamamı kaç saatte dolar?
4. Bir oyuncak, 60 TL’ye satılıyor. %20 indirim uygulanırsa yeni fiyatı kaç TL olur?

Rasyonel Sayılarla İşlemler Örnek Sorular Testi

1. Aşağıdaki işlemlerden hangisinin sonucu doğrudur?

2. Bir öğrenci, günlük 5/6 saat ders çalışıyor. 3 günde toplam kaç saat ders çalışır?

​

4. Aşağıdaki işlemlerden hangisinin sonucu en büyüktür?

7. Bir manav, 3/4 kg elmayı 2 müşteriye eşit olarak paylaştırıyor. Her müşteri kaç kg elma alır?

8. Bir kitapçı, bir kitabı önce 1/4 oranında indirime sokuyor, ardından kalan fiyatın 1/5’ini daha indiriyor. Başlangıçta 200 TL olan kitabın yeni fiyatı kaç TL olur?

A) 120 TL
B) 125 TL
C) 135 TL
D) 140 TL

10. Bir çiftçi 4/7 hektarlık bir tarlanın 2/3’ünü mısır tarlası olarak ayırmıştır. Çiftçi kaç hektar mısır tarlası ekmiştir?

Cevap Anahtarı

1 – B
2 – B
3 – A
4 – D
5 – B
6 – C
7 – A
8 – B
9 – B
10 – A