9. Sınıf Matematik Sayılar Konu Anlatımı Ve Örnek Sorular

Matematiğin temeli olan sayılar, günlük yaşantımızdan bilimsel hesaplamalara kadar her alanda karşımıza çıkar. Bu ünitede; doğal sayılar, tam sayılar, rasyonel sayılar, irrasyonel sayılar ve reel sayılar gibi sayı kümeleriyle tanışacak, sayıların özelliklerini ve aralarındaki ilişkileri öğreneceksiniz. Bu bilgiler, ileriki matematik konularını daha kolay anlamanızı sağlayacak güçlü bir temel oluşturur.

Sayılar yalnızca hesap yapmamıza değil, aynı zamanda mantıklı düşünme, genelleme yapma ve soyut düşünce becerilerimizi geliştirmemize yardımcı olur. Bu nedenle bu ünite, matematiğe sağlam bir giriş yapmanızı sağlayacak ilk adımdır.

1. Doğal Sayılar ve Özellikleri

• Tanım: Doğal sayılar, 0’dan başlayarak sonsuza kadar giden, negatif olmayan tam sayılardır.
  Sembol: N={0,1,2,3,… }

• Toplama, çıkarma ve çarpma işlemleri doğal sayılar kümesi içinde kapalıdır.
  Ancak çıkarma işlemi her zaman doğal sayılar içinde kalmaz. Örneğin:
  3−5=−2 doğal sayı değildir.

Örnek:

2. Tam Sayılar

• Tanım: Negatif ve pozitif doğal sayılar ile sıfırın birleşimi tam sayılar kümesini oluşturur.
  Sembol: Z={…,−3,−2,−1,0,1,2,3,… }

• Toplama, çıkarma, çarpma işlemleri tam sayılar kümesinde yapılabilir.
  Bölme işlemi her zaman tam sayı olmayabilir. Örneğin:
  4÷2=2 (Tam sayı)
  5÷2=2.5 (Tam sayı değil)

Örnek:

3. Rasyonel Sayılar

• Tanım: Payı ve paydası tam sayı olan, paydası sıfırdan farklı olan kesirli sayılara rasyonel sayı denir.
  Sembol: Q

• Her tam sayı bir rasyonel sayıdır. Örneğin: ​

• Ondalık sayılar da rasyonel olabilir.
  Örneğin: ​

Örnek:

​

4. İrrasyonel Sayılar

• Tanım: Virgülden sonra kesirli olmayan, sonsuz ve düzensiz devam eden ondalık sayılardır. Kesir şeklinde yazılamazlar.
  Sembol: R−Q

• En bilinen irrasyonel sayılar:
  

Örnek:

5. Reel Sayılar

• Tanım: Rasyonel ve irrasyonel sayıların birleşimiyle oluşan sayı kümesidir.
  Sembol: R

• Sayı doğrusu üzerindeki tüm sayılar bu kümede yer alır.
  

Örnek:

6. Sayı Kümeleri Arasındaki İlişkiler

• Doğal Sayılar ⊂ Tam Sayılar ⊂ Rasyonel Sayılar ⊂ Reel Sayılar

• Tüm doğal sayılar tam sayıdır ama tüm tam sayılar doğal sayı değildir.

• Her rasyonel sayı reel sayıdır ama her reel sayı rasyonel değildir.

Örnek Sıralama:

9. Sınıf Matematik Sayılar Ünitesi Testi

1. Aşağıdaki sayılardan hangisi irrasyonel bir sayıdır?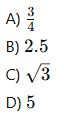

2. Aşağıdakilerden hangisi bir doğal sayı değildir?
A) 0
B) 7
C) -3
D) 2

4. ​ ifadesi aşağıdaki hangi kümede yer alır?
A) Sadece irrasyonel
B) Tam sayı ve rasyonel
C) Sadece doğal sayı
D) Hiçbir kümede

5. −5 sayısı aşağıdaki kümelerin hangisinde yer almaz?

6. 0.333 ondalık sayısı hangi sayı kümesindedir?
A) Sadece rasyonel
B) Sadece irrasyonel
C) Rasyonel ve tam sayı
D) Doğal sayı

7. Aşağıdakilerden hangisi reel sayı değildir?

8. Rasyonel sayı olmayan bir ifade aşağıdakilerden hangisidir?

9. Aşağıdaki sayı kümelerinin doğru sıralaması hangisidir?

10. Aşağıdaki ifadelerden hangisi yanlıştır?
A) Her doğal sayı tam sayıdır.
B) Her rasyonel sayı reel sayıdır.
C) Her tam sayı irrasyoneldir.
D) Her irrasyonel sayı reel sayıdır.

Cevap Anahtarı:

1. C

2. C

3. C

4. B

5. C

6. A

7. D

8. C

9. B

10. C