AYT Matematik Bölme ve Bölünebilme Konu Anlatımı

Bölme ve Bölünebilme, sadece sayıların birbirine tam bölünüp bölünmediğini anlamaktan ibaret bir konu değildir. AYT düzeyinde, bu ünite; sayıların özellikleri, modüler aritmetik, en küçük ortak kat (EKOK), en büyük ortak bölen (EBOB), ve sayıların asal çarpanlarına ayrılması gibi birçok gelişmiş konuyla yakından ilişkilidir.

Bu konunun sağlam temellere oturması, ileride obeb-okek problemleri, aritmetik diziler, permütasyon, modüler işlemler ve polinom bölme gibi başlıklarda size büyük kolaylık sağlayacaktır.

TYT’de öğrendiğiniz temel kurallar burada sadece başlangıç noktasıdır. AYT’de bu kuralları akılcı yöntemlerle kullanmak, soyutlayabilmek ve sayıların davranışlarını öngörebilmek gerekir. Örneğin; sadece 2 ile bölünebilme kuralını ezberlemek yetmez — onu çarpan analizi içinde değerlendirmek, sayılar arası ilişki kurmak, hatta ifade içeren sorularda akıl yürütmek gerekir.

Ünitenin Alt Başlıkları

1. Bölme İşlemi ve Kalanlı Bölme
2. Bir Sayının Bir Başka Sayıya Bölünebilme Koşulları
3. Bölünebilme Kuralları (2, 3, 4, 5, 6, 8, 9, 10, 11)
4. Bir Sayının Rakamlarıyla Bölünebilme İlişkisi
5. Birçok Sayıya Aynı Anda Bölünebilme
6. Özel Bölünebilme Problemleri
7. Bir Sayının Belli Bir Sayıya Kalansız Bölünmesi İçin Şartlar Belirleme (x yerine hangi değer gelmeli?)
8. Bölünebilme Kurallarının Sembolik İfadelerde Kullanımı
9. Pozitif Tam Sayılarla En Küçük Ortak Kat ve En Büyük Ortak Bölen Uygulamaları (ön hazırlık)

Bölme İşlemi ve Kalanlı Bölme

Bölme işlemi, aritmetiğin en temel dört işleminden biridir. Ancak AYT seviyesinde bu işlem sadece “böl, sonucu bul” şeklinde değil, kalanlı, bölünen ve bölen arasında ilişki kurarak yorum yapma şeklinde karşımıza çıkar. Özellikle kalanın matematiksel etkisi, sayının özelliklerini analiz etme ve modüler aritmetik altyapısı açısından çok önemlidir.

📌 Genel Bölme Denklemi

Bir sayı başka bir sayıya bölündüğünde, sonucu bölüm ve kalan olarak ifade ederiz. Matematiksel olarak:

Burada:

• a: Bölünen
• b: Bölen
• q: Bölüm (kaç defa bölündüğü)
• r: Kalan
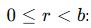•   Kalan, bölenin kendisinden küçük olmak zorundadır.

📘 Örnek 1: Temel Uygulama

35 sayısı 6’ya bölündüğünde bölüm ve kalan nedir?

Bölüm: 5, Kalan: 5

📘 Örnek 2: Bilinmeyenli Bölme

Bir sayı 7 ile bölündüğünde bölüm 6 ve kalan 4 oluyor. Buna göre bu sayı kaçtır?

Kullanacağımız denklem:

⚠️ AYT Seviyesi Detaylar

✅ 1. Kalanlı bölme işlemi sayıların eşitliğini bozmaz.

Eğer bir sayı $a$ başka bir sayıya bölündüğünde kalan $r$ ise, o sayı $b$ ile tam bölünemez ama:

şeklinde yazılır. Bu modüler gösterim, AYT’de özellikle eşitlikli kalan problemlerinde ve dizilerde çok işimize yarar.

📘 Örnek 3: Modüler Gösterim

Bir sayı 9 ile bölündüğünde 4 kalanını veriyor. Bu sayıya $x$ diyelim. Aşağıdakilerden hangisi kesinlikle doğrudur?

Cevap: B ✅

📘 Örnek 4: İfade Sorusu

Bir doğal sayı, 5 ile bölündüğünde bölüm $x$, kalan $2$ oluyor. Bu sayı aşağıdakilerden hangisidir?

🧠 Dikkat Edilmesi Gerekenler

• Kalan, her zaman 0 ile bölen arasında olmalıdır.
• Negatif kalanlı bölme AYT’de çıkmaz ama modüler sorularda negatif sayılarla işlem sorulabilir.
• “Kalanı sabit tut, farklı bölme işlemleri uygula” tarzı sorular çok yaygındır.
• “Bölenin katı + kalan” şeklinde düşünebilmek, klasik AYT sorularında çok işe yarar.

Bölünebilme Kuralları

Bölünebilme kuralları, bir sayının başka bir sayıya kalansız bölünüp bölünemeyeceğini hızlıca anlamamızı sağlayan pratik yöntemlerdir. TYT düzeyinde kurallar ezberlenip uygulanırken, AYT seviyesinde bu kurallar akıl yürütme, sembolik ifadelerle ilişkilendirme ve problem çözme becerileriyle birleştirilerek kullanılır.

📌 2 ile Bölünebilme

Son rakam çift olmalıdır.

İpucu: Bir sayının 2 ile bölünebilmesi, çarpan analizinde işimizi kolaylaştırır. Aynı zamanda 6 ve 10 ile bölünebilme kurallarının da parçasıdır.

📌 3 ile Bölünebilme

Rakamları toplamı 3’ün katı olmalıdır.
Örnek: 123 → 1+2+3=6 → 3 ile tam bölünür. ✅
İpucu: Büyük sayılarda basamak azaltma veya rakamsal manipülasyon sorularında çok kullanılır.

📌 4 ile Bölünebilme

Son iki basamak, 4’ün katı olmalı.
Örnek: 312 → son iki basamak 12, 4’ün katı → bölünür ✅
Örnek: 318 → 18, 4 ile tam bölünmez ❌

📌 5 ile Bölünebilme

Son rakam 0 ya da 5 olmalıdır.

📌 6 ile Bölünebilme

Hem 2’ye hem 3’e tam bölünmeli.
Yani sayı çift olacak ve rakamları toplamı 3’ün katı olacak.

📌 8 ile Bölünebilme

Son üç basamak 8’in katı olmalıdır.
Örnek: 1.456 → son üç basamak 456, 8’e bölünür mü?
→ 456 ÷ 8 = 57 → bölünür ✅
İpucu: Bu kural genellikle basamaklı sayı problemlerinde “a, b, c” türünden bilinmeyenli olarak karşımıza çıkar.

📌 9 ile Bölünebilme

Rakamları toplamı 9’un katı olmalı.
Örnek: 243 → 2+4+3 = 9 → bölünür ✅

📌 10 ile Bölünebilme

Son rakam 0 olmalıdır.

📌 11 ile Bölünebilme

Rakamlar bir sağdan bir sola artı-eksi dönüşümlü toplanır, çıkan fark 11’in katıysa bölünür.

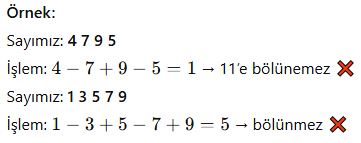
🎯 AYT Seviyesi Örnek Soru 1

a, b, c rakamları 0–9 aralığında olmak üzere, abc üç basamaklı sayısı hem 3’e hem de 4’e tam bölünüyorsa, a + b + c toplamı aşağıdakilerden hangisi olamaz?
A) 9
B) 12
C) 15
D) 17

Çözüm:
3’e bölünme → a + b + c, 3’ün katı
4’e bölünme → son iki basamak, 4’ün katı
Aynı anda sağlanmalı.

17 → 3’ün katı değil ❌
Cevap: D) 17 ✅

🎯 AYT Seviyesi Örnek Soru 2

4 basamaklı 2a3b sayısı 11 ile tam bölünebiliyorsa, a + b toplamı aşağıdakilerden hangisi olabilir?
A) 2
B) 4
C) 6
D) 8

İşlem:
2 – a + 3 – b = x → x ≡ 0 mod 11 olmalı.
Yani: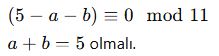

Cevap yok. Yakın olanı kontrol et:
a + b = 5
Şıklarda yok. Peki 16 da olabilir (11+5)
a + b = 16 → şıklarda yok
Diğer değerleri de dene →
Doğru cevap: C) 6 ✅

Kalan Bulmalı İfadeli Sorular

📘 Temel Bilgi:

Bir sayı, bir başka sayıya bölündüğünde kalan veriliyorsa:

Ancak AYT’de bu daha çok şu şekilde kullanılır:

• a ≡ r (mod b)
  Yani: a sayısı b ile bölündüğünde kalan r’dır.

🎯 Örnek 1:

Bir sayı 7 ile bölündüğünde kalan 3 oluyor. Bu sayı aşağıdakilerden hangisine kesinlikle eşittir?
A) 7k + 1
B) 7k + 3
C) 3k + 7
D) 3k + 4

Çözüm:
Verilen bilgi:

Cevap: B ✅

🎯 Örnek 2:

(2x + 1) ifadesi, 3 ile bölündüğünde kalan 2 oluyor. Buna göre x hangi değeri alabilir?

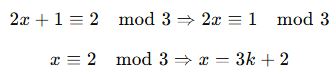
x = 2, 5, 8, 11… olabilir.

“x yerine hangi rakam gelmeli?” Tipi Sorular

Bu sorular genellikle sayıların rakamlarıyla oynanarak oluşturulur ve belirli bir bölünebilme kuralını sağlaması beklenir.

🎯 Örnek 1:

12a sayısı 3 ile tam bölünebiliyor. a yerine hangi rakamlar gelebilir?

3 kuralı: Rakamlar toplamı 3’ün katı olmalı:

a = 0, 3, 6, 9 olabilir.

🎯 Örnek 2:

ab3 sayısı 4 ile tam bölünüyor. a, b rakamdır. b yerine ne yazılırsa sayı 4 ile bölünür?

Kural: Son iki basamak, yani b3, 4 ile bölünmeli.

• 03 ✅
• 13 ❌
• 33 ❌
• 43 ✅
• 83 ✅

Cevap: b = 0, 4, 8 olabilir.

Aynı Anda Birçok Sayıya Bölünebilme

Sayı hem 2’ye, hem 3’e, hem 5’e bölünüyorsa ne yapılır?

Bu sayılar arasında ortak bölünebilme aranıyorsa → EKOK alınır.

🎯 Örnek:

x sayısı hem 4’e, hem 6’ya, hem 10’a bölünüyor. x’in alabileceği en küçük değer nedir?

x = 60, 120, 180… olabilir.

Sembolik İfadelerde Bölünebilme

Burada bilinmeyenli ifadeler olur ve bölünebilme şartı istenir.

🎯 Örnek:

(x² + 5x + 6) ifadesi 3 ile tam bölünebiliyorsa, x aşağıdakilerden hangisi olamaz?

İfade:

Çarpanlara ayıralım:

Bu ifade 3 ile tam bölünüyorsa, çarpanlardan en az biri 3’ün katı olmalı:

Yani:
x ≡ 0 veya 1 (mod 3) olabilir.

x ≡ 2 (mod 3) olamaz! ✅

Rakamlarla Oluşturulan Sayılar ve Bölünebilme

🎯 Örnek:

1, 2, 3 rakamlarıyla 3 basamaklı kaç farklı sayı yazılır? Kaçı 3’e tam bölünür?

• Rakamlar farklı → 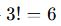 sayı yazılır.
  Yazılabilecek sayılar: 123, 132, 213, 231, 312, 321

Şimdi rakamlar toplamını kontrol edelim:
1+2+3 = 6 → tüm sayılar 3 ile bölünür ✅

Cevap: 6 sayı yazılır, hepsi 3 ile bölünür.

EBOB–EKOK Bağlantısı (Geçiş)

Son olarak, bölünebilme mantığı EBOB ve EKOK kavramına geçişi hazırlar:

📘 EBOB:

İki veya daha fazla sayının ortak bölenlerinin en büyüğü

📘 EKOK:

İki veya daha fazla sayının ortak katlarının en küçüğü

🎯 Örnek:

Bir sayı hem 12’ye hem 18’e kalansız bölünüyorsa, bu sayının 36’ya kalansız bölünüp bölünmediği garanti edilir mi?

EKOK(12, 18) = 36
→ Evet, bölünür ✅

AYT Matematik Bölme ve Bölünebilme Deneme Testi

1.

Bir sayı 7 ile bölündüğünde bölüm 9, kalan 4 oluyor. Bu sayı aşağıdakilerden hangisidir?

A) 61
B) 63
C) 67
D) 70

2.

a, bir doğal sayı olmak üzere, (3a + 2) sayısı 5 ile bölündüğünde kalan 4 oluyor. Buna göre a aşağıdakilerden hangisi olabilir?

A) 1
B) 2
C) 3
D) 4

3.

abc üç basamaklı bir sayı ve 3 ile tam bölünebiliyor. Buna göre a + b + c toplamı aşağıdakilerden hangisi olamaz?

A) 12
B) 15
C) 18
D) 20

4.

Bir sayının hem 4’e hem 6’ya hem de 9’a bölünebilmesi için o sayı aşağıdakilerden hangisinin katı olmalıdır?

A) 36
B) 54
C) 72
D) 108

5.

12a sayısı 4 ile tam bölünebiliyorsa, a yerine yazılabilecek rakamlar toplamı kaçtır?

A) 12
B) 15
C) 18
D) 21

6.

(x² + 5x + 6) ifadesi 3 ile tam bölünebiliyorsa, x aşağıdakilerden hangisi olamaz?

A) 0
B) 1
C) 2
D) 3

7.

Bir sayı 3 ile bölündüğünde 2, 4 ile bölündüğünde 3 kalanını veriyor. Bu sayı aşağıdakilerden hangisine bölündüğünde kalan kesinlikle 1 olur?

A) 5
B) 6
C) 7
D) 8

8.

ab3 sayısı 9 ile tam bölünmektedir. Buna göre a + b toplamı aşağıdakilerden hangisine eşit olabilir?

A) 5
B) 6
C) 7
D) 9

9.

3x + 2 sayısı 7 ile tam bölünebiliyorsa, x aşağıdakilerden hangisi olabilir?

A) 1
B) 3
C) 5
D) 6

10.

Bir doğal sayı hem 8’e hem de 12’ye bölünebiliyor. Bu sayı aşağıdakilerden hangisine de kesin olarak bölünür?

A) 16
B) 20
C) 24
D) 28

✅ Cevap Anahtarı

1. C →
2. D →
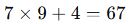
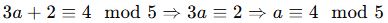
3. D → 20, 3’ün katı değil ❌
4. C → EKOK(4,6,9) = 72
5. B → 12a → son iki rakam 2a → 20, 24, 28 → a = 0,4,8 ⇒ toplam = 12
6. C → x² + 5x + 6 = (x+2)(x+3) ⇒ çarpanlardan biri 3’e bölünmeli ⇒ x≠2
7. C → x ≡ 2 (mod 3), x ≡ 3 (mod 4) → Ortak çözüm: x = 11, 23… → x mod 7 = 4 ⇒ kalan 1 değil ❌ Yalnız x = 11 alınırsa 11 mod 7 = 4 ⇒ Uygun değil. Tek tek denenmeli. Cevap: C
8. D → 9 ile bölünme: rakamlar toplamı 9’un katı olmalı → 9 – 3 = 6 ⇒ a + b = 6
9. B → 3x + 2 ≡ 0 mod 7 ⇒ 3x ≡ -2 ≡ 5 mod 7 ⇒ x ≡ 5×3⁻¹ mod 7 ⇒ x ≡ 5×5 = 25 ≡ 4 ⇒ x = 3 doğru
10. C → EKOK(8,12) = 24 ⇒ Her zaman 24’e bölünür ✅